华东师大版数学九年级上册 23.3直角三角形性质（课件）

这是一份华东师大版数学九年级上册 23.3直角三角形性质（课件），共14页。

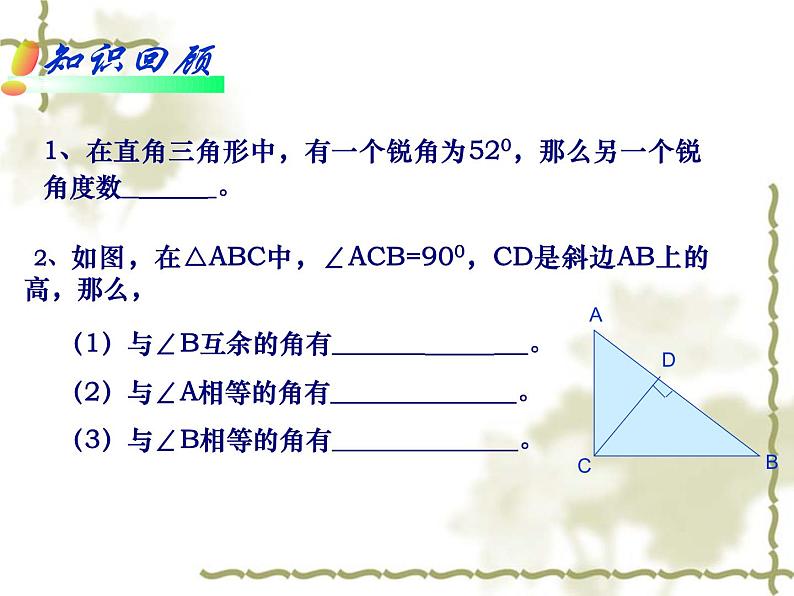
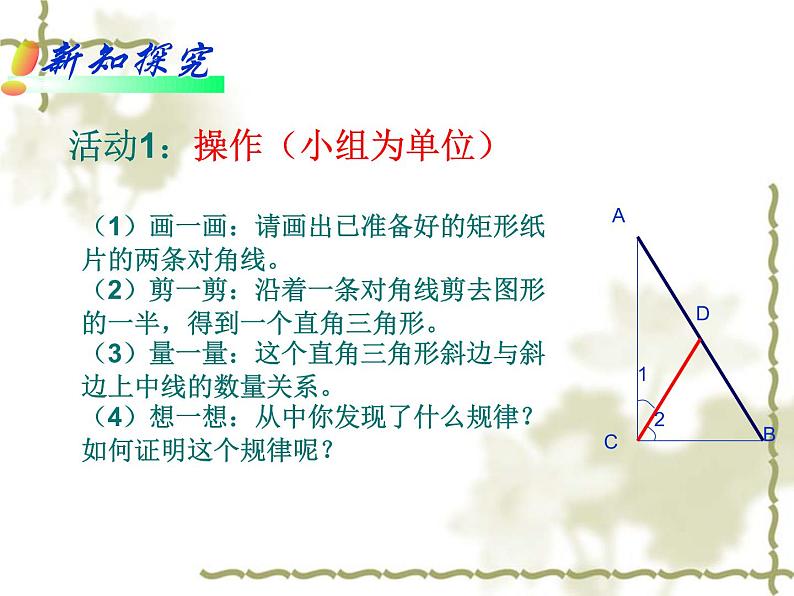
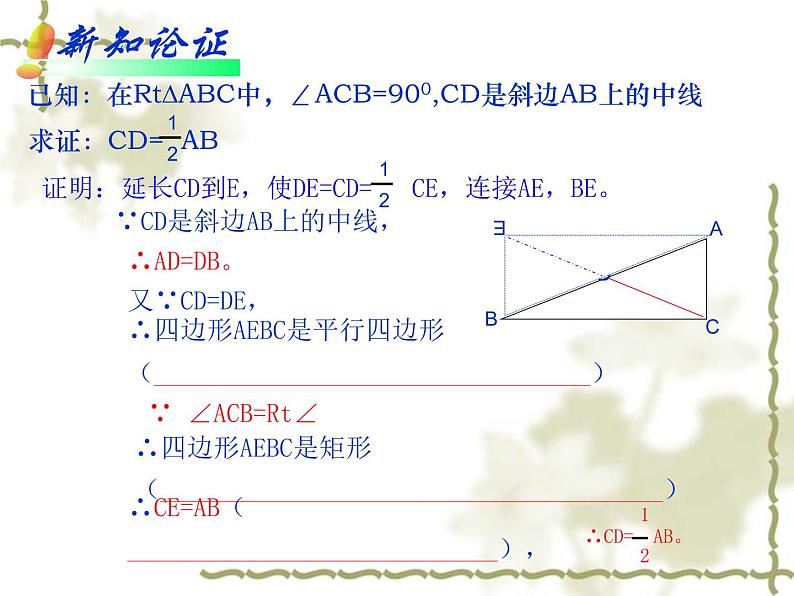
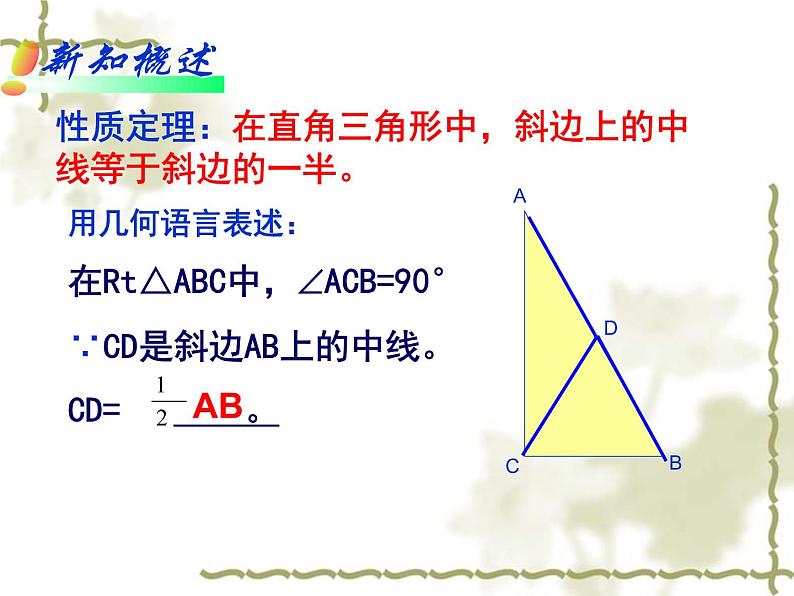
第24章解直角三角形2.直角三角形的性质什么是直角三角形？他的锐角有什么关系？他的三条边之间有什么关系？为什么？1、在直角三角形中，有一个锐角为520，那么另一个锐角度数         。    2、如图，在△ABC中，∠ACB=900，CD是斜边AB上的高，那么，    （1）与∠B互余的角有           。    （2）与∠A相等的角有           。    （3）与∠B相等的角有          。活动1：操作（小组为单位）（1）画一画：请画出已准备好的矩形纸片的两条对角线。（2）剪一剪：沿着一条对角线剪去图形的一半，得到一个直角三角形。（3）量一量：这个直角三角形斜边与斜边上中线的数量关系。（4）想一想：从中你发现了什么规律？如何证明这个规律呢？ 已知：在RtΔABC中，∠ACB=900,CD是斜边AB上的中线 求证：CD= AB证明：延长CD到E，使DE=CD= CE，连接AE，BE。 ∵CD是斜边AB上的中线，∴AD=DB。又∵CD=DE，∴四边形AEBC是平行四边形（_________________________________）∵ ∠ACB=Rt∠∴四边形AEBC是矩形（______________________________________）∴CE=AB（____________________________），性质定理：在直角三角形中，斜边上的中线等于斜边的一半。用几何语言表述：在Rt△ABC中，ACB=90°∵CD是斜边AB上的中线。CD= 。ABD活动2：探索300角所对的直角边与斜边的关系（1）拼一拼：用两个30度的同样大小的直角三角尺是否能拼出一个等边三角形。（2）议一议： 300角所对的直角边与斜边有什么关系？（3）说一说：你的猜想是什么？（4）想一想：如何证明这个猜想呢？ 推论：在直角三角形中，若一个锐角等于30度，它所对的直角边等于斜边的一半。CBAD已知：在RtΔABC中，∠ACB=900, ∠A=300 求证：BC= AB例 在ABC中，AB=AC，AD是△BAC的高，E、F分别是AB，AC的中点。问DE、DF有什么大小关系？分析：题中告诉了我们AB与AC相等的关系，要是能把DE、DF转化到AB与AC的问题就好了解 ∵AD是△BAC的高E、F分别是AB，AC的中点。直角三角形斜边上的中线等于斜边的一半) 又∵AB=AC ∴DE=DF练习1 在△ABC中， ∠ACB=90 °，CE是AB边上的中线，那么与CE相等的线段有_________，若∠A=35°，那么∠ECB= _________。练习2 在直角三角形中，斜边及其中线之和为6，那么该三角形的斜边长为________． 练习3 三角形三个内角之比为1：2：3，且最长边为4厘米，则最长边上的中线 厘米。AE、BE55°42判断（1）直角三角形两锐角互余 （ ）（2）在直角三角形中，斜边上的中线等于斜边的一半 （ ）（3）有两个角互余的三角形是直角三角形 （ ）（4）如果三角形一边上的中线等于这条边的一半，那么这个三角形是直角三角形。 （ ）√√√√1、 如图：在RtΔABC中，CD是斜边AB上的中线，已知∠DCA=200，则∠ A ＝＿＿，∠B＝____。∵CD是斜边AB上的中线∴CD=AD=BD= AB(直角三角形的斜边中线等于斜边的一半）∴∠Ａ＝∠ＤＣＡ＝２０°∴∠Ｂ＝９０°－ ∠Ａ＝ ９０°－２０°＝７０°（直角三角形两锐角互余）20°70°探究了直角三角形的性质1、两锐角互余。2、两直角边平方的和等于斜边的平方。3、斜边的中线等于斜边的一半。4、30度锐角所对的直角边等于斜边的一半。3、如图，已知BC=20m， ∠B=∠C=30°， E、G分别为AB，AC的中点，P为BC的中点，且EF⊥BC， GH⊥BC，垂足分别为F，H，求EF、PG的长；