初中数学人教版七年级下册第五章 相交线与平行线综合与测试同步训练题

这是一份初中数学人教版七年级下册第五章 相交线与平行线综合与测试同步训练题，共27页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

 《平行线与相交线》全章复习与巩固（培优篇）
（专项练习）
一、单选题
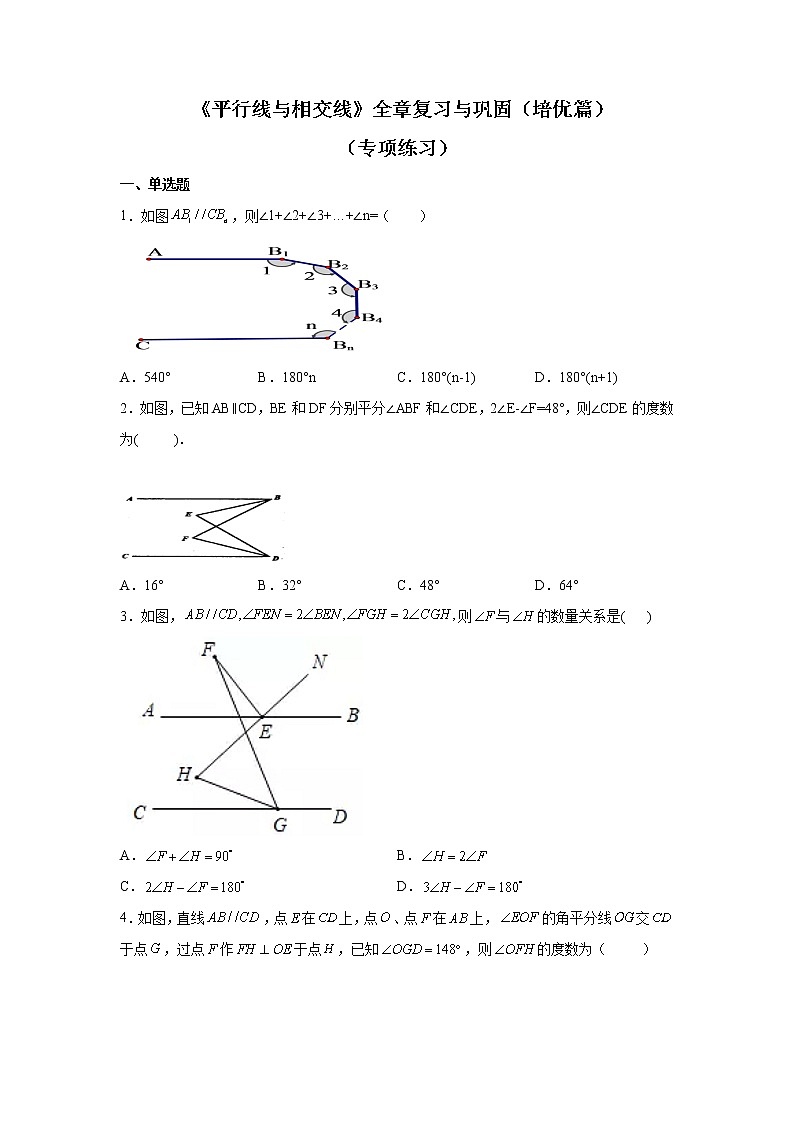
1．如图，则∠1+∠2+∠3+…+∠n=（ ）

A．540° B．180°n C．180°(n-1) D．180°(n+1)
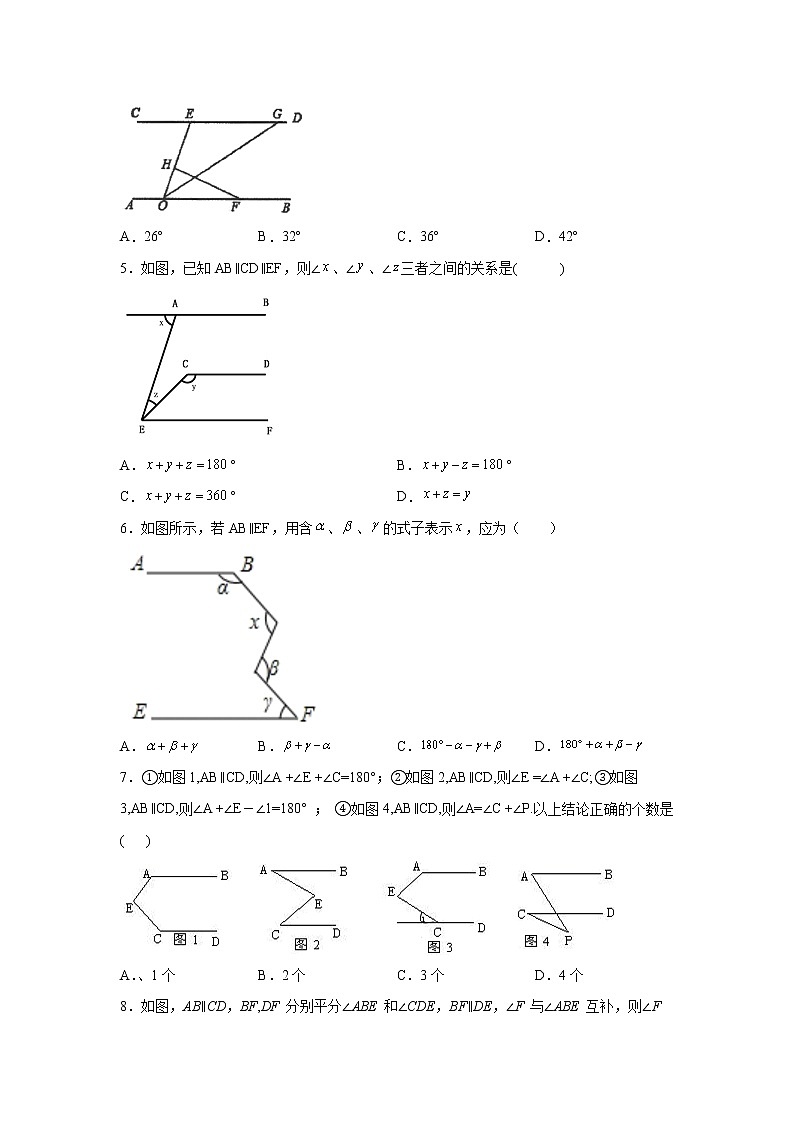
2．如图，已知AB∥CD，BE和DF分别平分∠ABF和∠CDE，2∠E-∠F=48°，则∠CDE的度数为( )．


A．16° B．32° C．48° D．64°
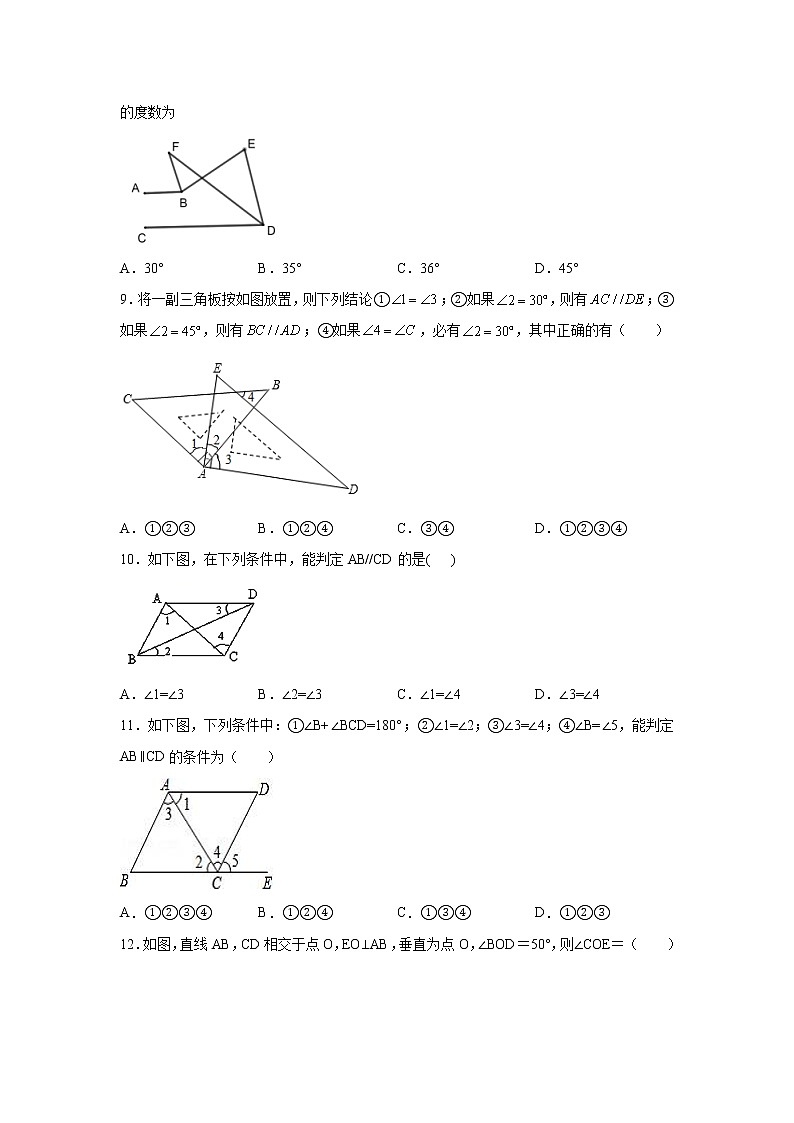
3．如图，则与的数量关系是( )

A． B．
C． D．
4．如图，直线，点在上，点、点在上，的角平分线交于点，过点作于点，已知，则的度数为（ ）

A．26º B．32º C．36º D．42º
5．如图，已知AB∥CD∥EF，则∠、∠、∠三者之间的关系是( )

A．° B．°
C．° D．
6．如图所示，若AB∥EF，用含、、的式子表示，应为（ ）

A． B． C． D．
7．①如图1,AB∥CD,则∠A +∠E +∠C=180°；②如图2,AB∥CD,则∠E =∠A +∠C;③如图3,AB∥CD,则∠A +∠E－∠1=180° ； ④如图4,AB∥CD,则∠A=∠C +∠P.以上结论正确的个数是( )

A．、1个 B．2个 C．3个 D．4个
8．如图，AB∥CD，BF,DF 分别平分∠ABE 和∠CDE，BF∥DE，∠F 与∠ABE 互补，则∠F 的度数为

A．30° B．35° C．36° D．45°
9．将一副三角板按如图放置，则下列结论①；②如果，则有；③如果，则有；④如果，必有，其中正确的有（ ）

A．①②③ B．①②④ C．③④ D．①②③④
10．如下图，在下列条件中，能判定AB//CD的是( )

A．∠1=∠3 B．∠2=∠3 C．∠1=∠4 D．∠3=∠4
11．如下图，下列条件中：①∠B+∠BCD=180°；②∠1=∠2；③∠3=∠4；④∠B=∠5，能判定AB∥CD的条件为（　　）

A．①②③④ B．①②④ C．①③④ D．①②③
12．如图，直线AB，CD相交于点O，EO⊥AB，垂直为点O，∠BOD＝50°，则∠COE＝（　　）

A．30° B．140° C．50° D．60°
13．如图，下列各式中正确的是（ ）

A． B．
C． D．


二、填空题
14．如图，直线MN∥PQ，点A在直线MN与PQ之间，点B在直线MN上，连结AB．∠ABM的平分线BC交PQ于点C，连结AC，过点A作AD⊥PQ交PQ于点D，作AF⊥AB交PQ于点F，AE平分∠DAF交PQ于点E，若∠CAE=45°，∠ACB=∠DAE，则∠ACD的度数是_____．

15．如图，已知AB∥CD,∠EAF =∠EAB,∠ECF=∠ECD ,则∠AFC与∠AEC之间的数量关系是_____________________________

16．如图，有两个正方形夹在AB与CD中，且AB//CD,若∠FEC=10°，两个正方形临边夹角为150°，则∠1的度数为________度(正方形的每个内角为90°)

17．如图，A、B、C表示三位同学所站位置，C同学在A同学的北偏东方向，在B同学的北偏西方向，那么C同学看A、B两位同学的视角______．

18．如图，平分平分，则 ______ ．

19．如图，一条公路修到湖边时，需拐弯绕湖而过，在A，B，C三处经过三次拐弯，此时道路恰好和第一次拐弯之前的道路平行(即AE∥CD)，若∠A=120°，∠B=150°,则∠C的度数是________

20．规律探究：同一平面内有直线、、，，，若，，，，，按此规律，与的位置关系是______．
21．与的两边互相垂直，且，则的度数为_________.
22．平面内不过同一点的条直线两两相交，它们交点个数记作，并且规定，则__________，____________．

三、解答题
23．如图①，已知AD∥BC，∠B=∠D=120°．
（1）请问：AB与CD平行吗？为什么？
（2）若点E、F在线段CD上，且满足AC平分∠BAE，AF平分∠DAE，如图②，求∠FAC的度数．
（3）若点E在直线CD上，且满足∠EAC=∠BAC，求∠ACD：∠AED的值（请自己画出正确图形，并解答）．


24．已知直线l1∥l2，直线l3和直线l1、l2交于点C和D，点P是直线l3上一动点
（1）如图1，当点P在线段CD上运动时，∠PAC，∠APB，∠PBD之间存在什么数量关系？请你猜想结论并说明理由．
（2）当点P在C、D两点的外侧运动时（P点与点C、D不重合，如图2和图3），上述（1）中的结论是否还成立？若不成立，请直接写出∠PAC，∠APB，∠PBD之间的数量关系，不必写理由．

25．如图，已知AM∥BN，∠A=60°，点P是射线M上一动点（与点A不重合），BC，BD分别平分∠ABP和∠PBN，分别交射线AM于点C，D,
（1）∠CBD=　 　
（2）当点P运动到某处时，∠ACB=∠ABD，则此时∠ABC=　 　
（3）在点P运动的过程中，∠APB与∠ADB的比值是否随之变化？若不变，请求出这个比值：若变化，请找出变化规律．




26．如图，已知直线l1∥l2，直线l3和直线l1、l2交于点C和D，点P是直线CD上的一个动点．
（1）如果点P运动到C、D之间时，试探究∠PAC，∠APB，∠PBD之间的关系，并说明理由．
（2）若点P在C、D两点的外侧运动时（P点与点C、D不重合），∠PAC，∠APB，∠PBD之间 的关系是否发生改变？请说明理由．












参考答案
1．C
【分析】
根据题意，作，，，由两直线平行，同旁内角互补，即可求出答案．
【详解】
解：根据题意，作，，，

∵，
∴，，，……
∴，……
∴；
故选：C．
【点拨】本题考查了平行线的性质，解题的关键是正确作出辅助线，熟练运用两直线平行同旁内角互补进行证明．
2．B
【分析】
已知BE和DF分别平分∠ABF和∠CDE，根据角平分线分定义可得∠ABE=∠ABF，∠CDF=∠CDE；过点E作EMAB，点F作FNAB，即可得EMFN，由平行线的性质可得∠ABE=∠BEM，∠MED=∠EDC，∠ABF=∠BFN，∠CDF=∠DFN，由此可得∠BED=∠BEM+∠DEM=∠ABE+∠CDE=∠ABF+∠CDE，∠BFD=∠BFN+∠DFN=∠ABF+∠CDF=∠ABF +∠CDE， 又因2∠BED-∠BFD=48°，即可得2（∠ABF+∠CDE）-（∠ABF +∠CDE）=48°，由此即可求得∠CDE=32°.
【详解】
∵BE和DF分别平分∠ABF和∠CDE，
∴∠ABE=∠ABF，∠CDF=∠CDE，
过点E作EMAB，点F作FNAB，

∵，
∴EMFN，
∴∠ABE=∠BEM，∠MED=∠EDC，∠ABF=∠BFN，∠CDF=∠DFN，
∴∠BED=∠BEM+∠DEM=∠ABE+∠CDE=∠ABF+∠CDE，
∠BFD=∠BFN+∠DFN=∠ABF+∠CDF=∠ABF +∠CDE，
∵2∠BED-∠BFD=48°，
∴2（∠ABF+∠CDE）-（∠ABF +∠CDE）=48°，
∴∠CDE=32°.
故选B.
【点拨】本题考查了平行线的性质，根据平行线的性质确定有关角之间的关系是解决问题的关键.
3．D
【分析】
先设角，利用平行线的性质表示出待求角，再利用整体思想即可求解．
【详解】
设
则
∵
∴






∴

故选：D．
【点拨】本题考查了平行线的性质，关键是熟练掌握平行线的性质，注意整体思想的运用．
4．A
【分析】
依据∠OGD=148°，可得∠EGO=32°，根据AB∥CD，可得∠EGO =∠GOF，根据GO平分∠EOF，可得∠GOE =∠GOF，等量代换可得：∠EGO=∠GOE=∠GOF=32°，根据，可得：=90°-32°-32°=26°
【详解】
解：∵ ∠OGD=148°,
∴∠EGO=32°
∵AB∥CD，
∴∠EGO =∠GOF,
∵的角平分线交于点,
∴∠GOE =∠GOF,
∵∠EGO=32°
∠EGO =∠GOF
∠GOE =∠GOF,
∴∠GOE=∠GOF=32°,
∵,
∴=90°-32°-32°=26°
故选A.
【点拨】本题考查的是平行线的性质及角平分线的定义的综合运用，易构造等腰三角形，用到的知识点为：两直线平行，内错角相等．
5．B
【分析】
根据平行线的性质可得∠CEF=180°-y，x=z+∠CEF，利用等量代换可得x=z+180°-y，再变形即可．
【详解】
解：∵CD∥EF，
∴∠C+∠CEF=180°，
∴∠CEF=180°-y，
∵AB∥CD，
∴x=z+∠CEF，
∴x=z+180°-y，
∴x+y-z=180°，
故选：B．
6．C
【分析】
过C作CD∥AB，过M作MN∥EF，推出AB∥CD∥MN∥EF，根据平行线的性质得出+∠BCD=180°，∠DCM=∠CMN，∠NMF=，求出∠BCD=180°-，∠DCM=∠CMN=-，即可得出答案．
【详解】
过C作CD∥AB，过M作MN∥EF，
∵AB∥EF，
∴AB∥CD∥MN∥EF，
∴+∠BCD=180°，∠DCM=∠CMN，∠NMF=，
∴∠BCD=180°-，∠DCM=∠CMN=-，
∴=∠BCD+∠DCM=，
故选：C．

【点拨】本题考查了平行线的性质的应用，主要考查了学生的推理能力．
7．C
【详解】
①如图1，过点E作EF∥AB，
因为AB∥CD，所以AB∥EF∥CD，
所以∠A+∠AEF=180°，∠C+∠CEF=180°，
所以∠A+∠AEC+∠C=∠A+∠AEF+∠C+∠CEF=180°+180°=360°，则①错误；
②如图2，过点E作EF∥AB，
因为AB∥CD，所以AB∥EF∥CD，
所以∠A=∠AEF，∠C=∠CEF，
所以∠A+∠C=∠AEC+∠AEF=∠AEC，则②正确；
③如图3，过点E作EF∥AB，
因为AB∥CD，所以AB∥EF∥CD，
所以∠A+∠AEF=180°，∠1=∠CEF，所以∠A+∠AEC-∠1=∠A+∠AEC-∠CEF=∠A+∠AEF=180°，则③正确；
④如图4，过点P作PF∥AB，因为AB∥CD，所以AB∥PF∥CD，
所以∠A=∠APF，∠C=∠CPF，所以∠A=∠CPF+∠APC=∠C+∠APC，则④正确；
故选C.

8．C
【分析】
延长BG交CD于G,然后运用平行的性质和角平分线的定义，进行解答即可.
【详解】
解：如图延长BG交CD于G

∵BF∥ED
∴∠F=∠EDF
又∵DF 平分∠CDE，
∴∠CDE=2∠F，
∵BF∥ED
∴∠CGF=∠EDF=2∠F，
∵AB∥CD
∴∠ABF=∠CGF=2∠F，
∵BF平分∠ABE
∴∠ABE=2∠ABF=4∠F，
又∵∠F 与∠ABE 互补
∴∠F +∠ABE =180°即5∠F=180°，解得∠F=36°
故答案选C.
【点拨】本题考查了平行的性质和角平分线的定义，做出辅助线是解答本题的关键.
9．D
【分析】
根据∠1+∠2=∠3+∠2即可证得①；根据求出∠1与∠E的度数大小即可判断②；利用∠2求出∠3，与∠B的度数大小即可判断③；利用求出∠1，即可得到∠2的度数，即可判断④.
【详解】
∵∠1+∠2=∠3+∠2=90，
∴∠1=∠3，故①正确；
∵，
∴
∠E=60，
∴∠1=∠E，
∴AC∥DE，故②正确；
∵，
∴，
∵,
∴∠3=∠B,
∴,故③正确；
∵，
∴∠CFE=∠C，
∵∠CFE+∠E=∠C+∠1，
∴∠1=∠E=,
∴∠2=90-∠1=，故④正确，
故选：D.

【点拨】此题考查互余角的性质，平行线的判定及性质，熟练运用解题是关键.
10．C
【详解】
根据平行线的判定，可由∠2=∠3，根据内错角相等，两直线平行，得到AD∥BC，由∠1=∠4，得到AB∥CD.
故选C.
11．C
【详解】
解：①∵∠B+∠BCD=180°，
∴AB∥CD；
②∵∠1=∠2，
∴AD∥BC；
③∵∠3=∠4，
∴AB∥CD；
④∵∠B=∠5，
∴AB∥CD；
∴能得到AB∥CD的条件是①③④．
故选C．
【点拨】此题主要考查了平行线的判定，解题关键是合理利用平行线的判定，确定同位角、内错角、同旁内角. 平行线的判定：同旁内角互补，两直线平行；内错角相等，两直线平行；
同位角相等，两直线平行.
12．B
【详解】
试题解析：EO⊥AB，



故选B.
13．D
【详解】
试题分析：延长TS，

∵OP∥QR∥ST，
∴∠2=∠4，
∵∠3与∠ESR互补，
∴∠ESR=180°﹣∠3，
∵∠4是△FSR的外角，
∴∠ESR+∠1=∠4，即180°﹣∠3+∠1=∠2，
∴∠2+∠3﹣∠1=180°．
故选D．
考点：平行线的性质．
14．27°．
【分析】
延长FA与直线MN交于点K，通过角度的不断转换解得∠BCA=45°.
【详解】
解：延长FA与直线MN交于点K，

由图可知∠ACD=90°-∠CAD=90°-(45°+∠EAD)=45°-∠FAD=45°-(90°-∠AFD)=∠AFD，
因为MN∥PQ，所以∠AFD=∠BKA=90°-∠KBA=90°-(180°-∠ABM)=∠ABM-90°，
所以∠ACD=∠AFD=(∠ABM-90°)=∠BCD-45°，即∠BCD-∠ACD=∠BCA=45°，
所以∠ACD=90°-(45°+∠EAD)=45°-∠EAD=45°-∠BCA=45°-18°=27°.
故∠ACD的度数是：27°.
【点拨】本题利用平行线、垂直、角平分线综合考查了角度的求解.
15．4∠AFC=3∠AEC
【详解】
【分析】连接AC，设∠EAF=x°，∠ECF=y°，∠EAB=4x°，∠ECD=4y°，根据平行线性质得出∠BAC+∠ACD=180°，求出∠CAE+∠ACE=180°-（4x°+4y°），求出∠AEC=4（x°+y°），∠AFC═3（x°+y°），即可得出答案．
【详解】连接AC，设∠EAF=x°，∠ECF=y°，∠EAB=4x°，∠ECD=4y°，
∵AB∥CD，
∴∠BAC+∠ACD=180°，
∴∠CAE+4x°+∠ACE+4y°=180°，
∴∠CAE+∠ACE=180°-（4x°+4y°），∠FAC+∠FCA=180°-（3x°+3y°），
∴∠AEC=180°-（∠CAE+∠ACE）
=180°-[180°-（4x°+4y°）]
=4x°+4y°
=4（x°+y°），
∠AFC=180°-（∠FAC+∠FCA）
=180°-[180°-（3x°+3y°）]
=3x°+3y°
=3（x°+y°），
∴∠AFC=∠AEC，
即：4∠AFC=3∠AEC，

故正确答案为：4∠AFC=3∠AEC.
【点睛】本题考查了平行线性质和三角形内角和定理的应用，注意：两直线平行，同旁内角互补．
16．70．
【详解】
作IF∥AB,GK∥AB,JH∥AB
因为AB∥CD
所以，AB∥CD∥ IF∥GK∥JH
所以，∠IFG=∠FEC=10°
所以，∠GFI=90°-∠IFG=80°
所以，∠KGF=∠GFI=80°
所以，∠HGK=150°-∠KGF=70°
所以，∠JHG=∠HGK=70°
同理，∠2=90°-∠JHG=20°
所以，∠1=90°-∠2=70°

故答案为70
【点拨】本题考查了平行线的性质，正确作出辅助线是关键，注意掌握平行线的性质：两直线平行，内错角相等．
17．
【解析】
【分析】
根据平行线的性质：两直线平行，内错角相等，可得答案．
【详解】
如图
，
作，
，
，
，
故答案为：．
【点拨】本题考查了方向角，利用平行线的性质两直线平行内错角相等是解题关键．
18．
【分析】
首先过点E作EM∥AB，过点F作FN∥AB，由AB∥CD，即可得EM∥AB∥CD∥FN，然后根据两直线平行，同旁内角互补，由∠BED=110°，即可求得∠ABE+∠CDE=250°，又由BF平分∠ABE，DF平分∠CDE，根据角平分线的性质，即可求得∠ABF+∠CDF的度数，又由两只线平行，内错角相等，即可求得∠BFD的度数．
【详解】
过点E作EM∥AB，过点F作FN∥AB，

∵AB∥CD，
∴EM∥AB∥CD∥FN，
∴∠ABE+∠BEM=180°，∠CDE+∠DEM=180°，
∴∠ABE+∠BED+∠CDE=360°，
∵∠BED=110°，
∴∠ABE+∠CDE=250°，
∵BF平分∠ABE，DF平分∠CDE，
∴∠ABF=∠ABE，∠CDF=∠CDE，
∴∠ABF+∠CDF=（∠ABE+∠CDE）=125°，
∵∠DFN=∠CDF，∠BFN=∠ABF，
∴∠BFD=∠BFN+∠DFN=∠ABF+∠CDF=125°．
故答案为125°
【点拨】此题考查了平行线的性质与角平分线的定义．此题难度适中，解题的关键是注意数形结合思想的应用，注意辅助线的作法．
19．150°
【详解】
如图，过点B作BG∥AE，
因为AE∥CD，所以AE∥BG∥CD.
所以∠A=∠2，∠1+∠C=180°.
因为∠A=120°，所以∠2=120°，所以∠1=150°-120°=30°.
所以∠C=180°-30°=150°，故答案为150°.

20．互相垂直．
【解析】
【分析】
依据，，，，，可得，即可得到与的位置关系是互相垂直．
【详解】
解：，，，
，
按此规律，，
又，，
，
以此类推，
，
，
故答案为：互相垂直．
【点拨】本题主要考查了平行线的性质，解决问题的关键是根据已知条件得出规律：．
21．130°或50°
【解析】
【分析】作图分析，若两个角的边互相垂直，那么这两个角必相等或互补，可据此解答．
【详解】如图∵β的两边与α的两边分别垂直，
∴α+β=180°
故β=130°，
在上述情况下，若反向延长∠β的一边，那么∠β的补角的两边也与∠α的两边互相垂直，故此时∠β=50；
综上可知：∠β=50°或130°，

故正确答案为：
【点睛】本题考核知识点：四边形内角和. 解题关键点：根据题意画出图形，分析边垂直的2种可能情况.
22．1. .
【分析】
条直线相交只有一个交点，条直线相交，交点数是，条直线相交，交点数是，即，可写出， 的解.
【详解】
解：求平面内不过同一点的条直线两两相交的交点个数，可由简入繁，
当2条直线相交时，交点数只有一个；
当3条直线相交时，交点数为两条时的数量第3条直线与前两条的交点2个，即交点数是；
同理，可以推导当n条直线相交时，交点数是，即
，
，
，
本题的答案为：1，.
【点拨】本题考查了平面内直线两两相交交点数的计算，涉及到一种很重要的数学方法数学归纳法的初步应用接触，此方法在推导证明中比较常用.
23．（1）平行，理由见解析；（2）∠FAC =30°；（3）∠ACD：∠AED=2：3或2：1．
【详解】
试题分析：（1）依据平行线的性质以及判定，即可得到AB∥CD；
（2）依据AC平分∠BAE，AF平分∠DAE，即可得到∠EAC=∠BAE，∠EAF=∠DAE，进而得出∠FAC=∠EAC+∠EAF=（∠BAE+∠DAE）=∠DAB；
（3）分两种情况讨论：当点E在线段CD上时；当点E在DC的延长线上时，分别依据AB∥CD，进而得到∠ACD：∠AED的值．
试题解析：解：（1）平行．
如图①．∵AD∥BC，∴∠A+∠B=180°．
又∵∠B=∠D=120°，∴∠D+∠A=180°，∴AB∥CD；

（2）如图②．∵AD∥BC，∠B=∠D=120°，∴∠DAB=60°．
∵AC平分∠BAE，AF平分∠DAE，∴∠EAC=∠BAE，∠EAF=∠DAE，
∴∠FAC=∠EAC+∠EAF=（∠BAE+∠DAE）=∠DAB=30°；

（3）①如图3，当点E在线段CD上时，
由（1）可得AB∥CD，∴∠ACD=∠BAC，∠AED=∠BAE．

又∵∠EAC=∠BAC，∴∠ACD：∠AED=2：3；
②如图4，当点E在DC的延长线上时，
由（1）可得AB∥CD，∴∠ACD=∠BAC，∠AED=∠BAE．
又∵∠EAC=∠BAC，∴∠ACD：∠AED=2：1．
综上所述：∠ACD：∠AED=2：3或2：1．
点睛：本题主要考查了平行线的性质以及判定，平行线的判定是由角的数量关系判断两直线的位置关系，平行线的性质是由平行关系来寻找角的数量关系．
24．（1）∠APB=∠PAC+∠PBD；(2)不成立
【分析】
（1）当P点在C、D之间运动时，首先过点P作PE∥l1，由l1∥l2，可得PE∥l2∥l1，根据两直线平行，内错角相等，即可求得：∠APB=∠PAC+∠PBD．
（2）当点P在C、D两点的外侧运动时，由直线l1∥l2，根据两直线平行，同位角相等与三角形外角的性质，即可求得：∠PAC=∠PBD+∠APB或∠PBD=∠PAC+∠APB．
【详解】
（1）如图1，当P点在C、D之间运动时，∠APB=∠PAC+∠PBD．

理由如下：
过点P作PE∥l1，
∵l1∥l2，
∴PE∥l2∥l1，
∴∠PAC=∠1，∠PBD=∠2，
∴∠APB=∠1+∠2=∠PAC+∠PBD；
（2）不成立
如图2，当点P在C、D两点的外侧运动，且在l2下方时，∠PAC=∠PBD+∠APB．
理由如下：
∵l1∥l2，
∴∠PED=∠PAC，
∵∠PED=∠PBD+∠APB，
∴∠PAC=∠PBD+∠APB．
如图3，当点P在C、D两点的外侧运动，且在l1上方时，∠PBD=∠PAC+∠APB．
理由如下：
∵l1∥l2，
∴∠PEC=∠PBD，
∵∠PEC=∠PAC+∠APB，
∴∠PBD=∠PAC+∠APB．
【点拨】考查平行线的判定与性质，三角形外角的性质等，三角形的一个外角等于与它不相邻的两个内角的和.
25．（1）60°；（2）30°；（3）不变．
【分析】
（1）由AM∥BN可得∠ABN=180°-∠A，再由BC、BD均为角平分线可求解；
（2）由AM∥BN可得∠ACB=∠CBN，再由∠ACB=∠ABD可得∠ABC =∠DBN；
（3）由AM∥BN可得∠APB=∠PBN，再由BD为角平分线即可解答.
【详解】
解：（1）∵AM∥BN，
∴∠ABN=180°﹣∠A=120°，
又∵BC，BD分别平分∠ABP和∠PBN，
∴∠CBD=∠CBP+∠DBP=（∠ABP+∠PBN）=∠ABN=60°，
故答案为60°．
（2）∵AM∥BN，
∴∠ACB=∠CBN，
又∵∠ACB=∠ABD，
∴∠CBN=∠ABD，
∴∠ABC=∠ABD﹣∠CBD=∠CBN﹣∠CBD=∠DBN，
∴∠ABC=∠CBP=∠DBP=∠DBN，
∴∠ABC=∠ABN=30°，
故答案为30°．
（3）不变．理由如下：
∵AM∥BN，
∴∠APB=∠PBN，∠ADB=∠DBN，
又∵BD平分∠PBN，
∴∠ADB=∠DBN=∠PBN=∠APB，即∠APB：∠ADB=2：1．
【点拨】本题考查了平行线的性质.
26．（1）P点在C、D之间运动时，则有∠APB＝∠PAC+∠PBD，理由详见解析；（2）详见解析.
【分析】
（1）当P点在C、D之间运动时，首先过点P作，由，可得,根据两直线平行，内错角相等，即可求得: ∠APB＝∠PAC+∠PBD；
（2）当点P在C、D两点的外侧运动时，则有两种情形，由直线，根据两直线平行,内错角相等，同位角相等与三角形外角的性质，可分别求得:∠APB＝∠PAC－∠PBD和∠APB＝∠PBD-∠PAC.
【详解】
解：（1）若P点在C、D之间运动时，则有∠APB＝∠PAC+∠PBD.理由是：
如图，过点P作PE∥l1，则∠APE＝∠PAC，
又因为l1∥l2，所以PE∥l2，
所以∠BPE＝∠PBD，
所以∠APE+∠BPE＝∠PAC+∠PBD，
即∠APB＝∠PAC+∠PBD.
（2）若点P在C、D两点的外侧运动时（P点与点C、D不重合），则有两种情形：
①如图1，有结论：∠APB＝∠PAC－∠PBD.理由是：
过点P作PE∥l1，则∠APE＝∠PAC
又因为l1∥l2，所以PE∥l2
所以∠BPE＝∠PBD
所以∠APB＝∠APE-∠BPE
即∠APB＝∠PAC－∠PBD.
②如图2，有结论：∠APB＝∠PBD－∠PAC.理由是：
过点P作PE∥l2，则∠BPE＝∠PBD
又因为l1∥l2，所以PE∥l1
所以∠APE＝∠PAC
所以∠APB＝∠BPE-∠APE
即∠APB＝∠PBD-∠PAC.

【点拨】本题主要考查平行线的性质与三角形外角的性质.此题难度适中,解题的关键是掌握两直线平行,内错角相等与两直线平行,同位角相等,注意辅助线的作法