初中数学人教版七年级下册第五章 相交线与平行线综合与测试一课一练

《平行线与相交线》全章复习与巩固（知识讲解）

【学习目标】

1．   熟练掌握对顶角，邻补角及垂线的概念及性质，了解点到直线的距离与两平行线间的距离的概念；

2. 区别平行线的判定与性质，并能灵活运用；

3. 了解命题的概念及构成，并能通过证明或举反例判定命题的真假；

4. 了解平移的概念及性质.

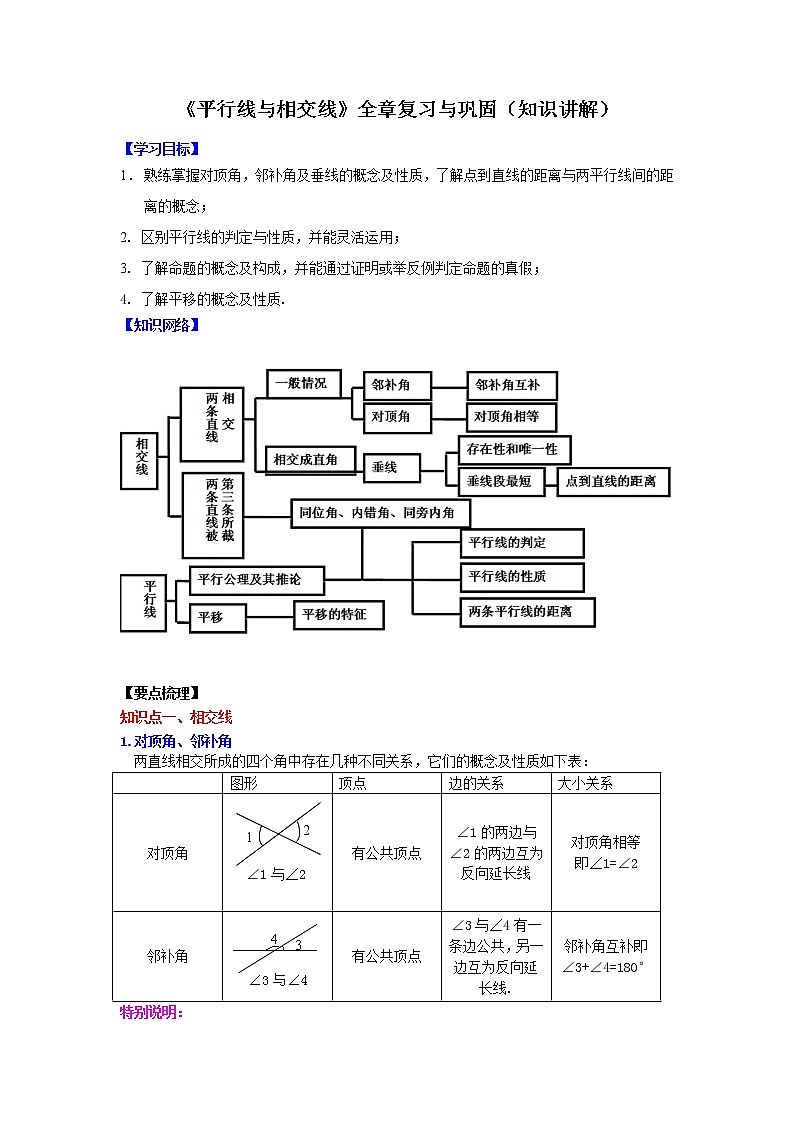
【知识网络】

【要点梳理】

知识点一、相交线

1.对顶角、邻补角

两直线相交所成的四个角中存在几种不同关系，它们的概念及性质如下表：

特别说明：

⑴对顶角是成对出现的，对顶角是具有特殊位置关系的两个角.对顶角的特征:有公共顶点，角的两边互为反向延长线.

⑵如果∠α与∠β是对顶角，那么一定有∠α=∠β；反之如果∠α=∠β，那么∠α与∠β不一定是对顶角.

⑶如果∠α与∠β互为邻补角，则一定有∠α+∠β=180°；反之如果∠α+∠β=180°，则∠α与∠β不一定是邻补角.邻补角的特征:有公共顶点，有一条公共边，另一边互为反向延长线．

⑶两直线相交形成的四个角中，每一个角的邻补角有两个，而对顶角只有一个.

2.垂线及性质、点到直线的距离

（1）垂线的定义：

当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，其中的一条直线叫做另一条直线的垂线，它们的交点叫做垂足.如图1所示，符号语言记作： AB⊥CD，垂足为O.

特别说明：

要判断两条直线是否垂直，只需看它们相交所成的四个角中，是否有一个角是直角，两条线段垂直，是指这两条线段所在的直线垂直.

（2）垂线的性质：

垂线性质1：在同一平面内，过一点有且只有一条直线与已知直线垂直 (与平行公理相比较记).

垂线性质2：连接直线外一点与直线上各点的所有线段中，垂线段最短.简称：垂线段最短.

（3）点到直线的距离：

直线外一点到这条直线的垂线段的长度，叫做点到直线的距离，如图2：PO⊥AB，点P到直线AB的距离是垂线段PO的长.

特别说明：垂线段PO是点P到直线AB所有线段中最短的一条.

知识点二、平行线

1．平行线的判定

判定方法1：同位角相等，两直线平行．

判定方法2：内错角相等，两直线平行．

判定方法3：同旁内角互补，两直线平行．

特别说明：根据平行线的定义和平行公理的推论，平行线的判定方法还有：

（1）平行线的定义：在同一平面内，如果两条直线没有交点（不相交），那么两直线平行.

（2）如果两条直线都平行于第三条直线，那么这两条直线平行（平行线的传递性）.

（3）在同一平面内，垂直于同一直线的两条直线平行.

（4）平行公理：经过直线外一点，有且只有一条直线与这条直线平行.

2．平行线的性质

性质1：两直线平行，同位角相等；

性质2：两直线平行，内错角相等；

性质3：两直线平行，同旁内角互补.

特别说明：根据平行线的定义和平行公理的推论，平行线的性质还有：

（1）若两条直线平行，则这两条直线在同一平面内，且没有公共点．

（2）如果一条直线与两条平行线中的一条直线垂直，那么它必与另一条直线垂直．

3．两条平行线间的距离

如图3，直线AB∥CD，EF⊥AB于E，EF⊥CD于F，则称线段EF的长度为两平行线AB与CD间的距离.

特别说明：

（1）两条平行线之间的距离处处相等.

（2）初中阶级学习了三种距离,分别是两点间的距离、点到直线距离、平行线间的距离.这三种距离的共同点在于都是线段的长度,它们的区别是两点间的距离是连接这两点的线段的长度,点到直线距离是直线外一点引已知直线的垂线段的长度, 平行线间的距离是一条直线上的一点到与之平行的另一直线的距离.

（3）如何理解 “垂线段”与 “距离”的关系：垂线段是一个图形，距离是线段的长度，是一个量，它们之间不能等同.

知识点三、命题及平移

1.命题：判断一件事情的语句，叫做命题．每个命题都由题设、结论两部分组成.题设是已知事项；结论是由已知事项推出的事项.

2.平移：在平面内，将一个图形沿某个方向移动一定的距离，图形的这种移动叫做平移．

特别说明：平移的性质：

（1）平移后，对应线段平行（或共线）且相等；

（2）平移后，对应角相等；

（3）平移后，对应点所连线段平行（或共线）且相等；

（4）平移后，新图形与原图形是一对全等图形.

【典型例题】

类型一、相交线 

1. 如图，与是同位角的是__________．

【答案】①②

【分析】根据同位角的定义：在截线的同侧，并且在被截线的同一方的两个角是同位角．

解：这四个图中，∠1与∠2有一条边在同一条直线上，另一条边在被截线的同一方，是同位角，符合的有图①②．

故答案为：①②．

【点拨】本题考查了同位角、内错角、同旁内角．解答此类题确定三线八角是关键，可直接从截线入手．对平面几何中概念的理解，一定要紧扣概念中的关键词语，要做到对它们正确理解，对不同的几何语言的表达要注意理解它们所包含的意义．

举一反三：

【变式】如图，有下列3个结论：①能与∠DEF构成内错角的角的个数是2；②能与∠EFB构成同位角的角的个数是1；③能与∠C构成同旁内角的角的个数是4，以上结论正确的是_____．

【答案】①②．

【分析】根据同位角的边构成“F“形，内错角的边构成“Z“形，同旁内角的边构成“U”形进行判定．

解：①能与构成内错角的角的个数有2个，即和，故正确；

②能与构成同位角的角的个数只有1个：即，故正确；

③能与构成同旁内角的角的个数有5个：即，，，，，故错误；

所以结论正确的是①②．

故答案为：①②．

【点拨】本题主要考查了同位角、内错角、同旁内角，熟记“三线八角”中相关的定义和概念，掌握同位角的边构成“F“形，内错角的边构成“Z“形，同旁内角的边构成“U”形是解答此题的关键．

2. 如图，直线AB、CD相交于点O，OM⊥AB

(1) 若∠1＝∠2，求∠NOD的度数

(2) 若∠1＝∠BOC，求∠AOC和∠MOD的度数

【答案】（1）90°；（2）∠AOC=60°，∠MOD＝150°.

【分析】（1）由垂线的性质求得∠AOM=∠BOM=90°，然后根据等量代换及邻补角的定义解答；
（2）根据垂直的定义求得∠AOM=∠BOM=90°，再由∠1=∠BOC求得∠BOC=120°；然后根据邻补角定义和对顶角的性质即可求解．

解：(1) ∵OM⊥AB，∠1＝∠2，

∴∠1＋∠AOC＝∠2＋∠AOC＝90°，即∠CON＝90°，

∴ON⊥CD，

∴∠NOD＝90°

(2)   ∵OM⊥AB，∠1＝∠BOC，

∴∠1＝30°，∠BOC＝120°，

又∵∠AOC＋∠BOC＝180°，

∴∠AOC＝60°，

∵∠1＋∠MOD＝180°，

∴∠MOD＝150°

【点拨】本题利用垂直的定义，对顶角的性质和邻补角的定义计算，要注意领会由垂直得直角这一要点．

【变式】如图，直线AB、CD相交于点O，OE平分∠BOD．

（1）若∠AOC=70°，∠DOF=90°，求∠EOF的度数；

（2）若OF平分∠COE，∠BOF=15°，若设∠AOE=x°．

①用含x的代数式表示∠EOF；

②求∠AOC的度数．

【答案】（1）55°（2）①x②100°

【分析】（1）由对顶角的性质可知∠BOD=70°，从而可求得∠FOB=20°，由角平分线的定义可知∠BOE=∠BOD，最后根据∠EOF=∠BOE+∠FOB求解即可；
（2）①先证明∠AOE=∠COE= x°，然后由角平分线的定义可知∠FOE=x°；
②∠BOE=∠FOE-∠FOB可知∠BOE=x°-15°，最后根据∠BOE+∠AOE=180°列出方程可求得x的值，从而可求得∠AOC的度数．

解：（1）由对顶角相等可知：∠BOD=∠AOC=70°，
∵∠FOB=∠DOF-∠BOD，

∴∠FOB=90°-70°=20°，
∵OE平分∠BOD，

∴∠BOE=∠BOD=×70°=35°，
∴∠EOF=∠FOB+∠BOE=35°+20°=55°；
（2）①∵OE平分∠BOD，
∴∠BOE=∠DOE，
∵∠BOE+∠AOE=180°，∠COE+∠DOE=180°，

∴∠COE=∠AOE=x°，
∵OF平分∠COE，

∴∠EOF=x°；
②∵∠BOE=∠FOE-∠FOB，

∴∠BOE=x°-15°，
∵∠BOE+∠AOE=180°，

∴x°-15°+x°=180°，解得：x=130，
∴∠AOC=2∠BOE=2×（180°-130°）=100°．

【点拨】本题考查对顶角，邻补角以及角平分线定义，主要考查学生的计算能力，熟练掌握角平分线的定义是解题的关键．

类型二、平行线的性质与判定

3.已知：如图，AE⊥BC，FG⊥BC，∠1＝∠2，∠D＝∠3＋60°，∠CBD＝70°．

（1）求证：AB∥CD；

（2）求∠C的度数．

【答案】（1）见解析；（2）25°

【分析】（1）求出AE∥GF，求出∠2＝∠A＝∠1，根据平行线的判定推出即可；

（2）根据平行线的性质得出∠D＋∠CBD＋∠3＝180°，求出∠3，根据平行线的性质求出∠C即可．

 （1）证明：∵AE⊥BC，FG⊥BC，

∴AE∥GF，

∴∠2＝∠A，

∵∠1＝∠2，

∴∠1＝∠A，

∴AB∥CD；

（2）解：∵AB∥CD，

∴∠D＋∠CBD＋∠3＝180°，

∵∠D＝∠3＋60°，∠CBD＝70°，

∴∠3＝25°，

∵AB∥CD，

∴∠C＝∠3＝25°．

【点拨】本题考查了平行线的性质和判定的应用，牢记：平行线的性质有：①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补，反之亦成立．

举一反三：

【变式1】如图所示，已知，试判断与的大小关系，并说明理由.

【答案】.

【分析】首先判断∠AED与∠ACB是一对同位角，然后根据已知条件推出DE∥BC，得出两角相等．

解：∠AED=∠ACB．

理由：如图，分别标记∠1，∠2，∠3，∠4.

∵∠1+∠4=180°（平角定义），∠1+∠2=180°（已知）．
∴∠2=∠4．
∴EF∥AB（内错角相等，两直线平行）．
∴∠3=∠ADE（两直线平行，内错角相等）．
∵∠3=∠B（已知），
∴∠B=∠ADE（等量代换）．
∴DE∥BC（同位角相等，两直线平行）．
∴∠AED=∠ACB（两直线平行，同位角相等）．

【点拨】本题重点考查平行线的性质和判定，难度适中．

【变式1】如图，已知DG⊥BC，AC⊥BC，EF⊥AB，∠1=∠2，求证：CD⊥AB

【答案】见解析；

【分析】灵活运用垂直的定义，注意由垂直可得90°角，由90°角可得垂直，结合平行线的判定和性质，只要证得∠ADC=90°，即可得CD⊥AB．

 证明：∵ DG⊥BC，AC⊥BC（已知），

∴ ∠DGB=∠ACB=90°（垂直的定义），

∴ DG∥AC（同位角相等，两直线平行）.

∴ ∠2=∠ACD（两直线平行，内错角相等）.

∵ ∠1=∠2（已知），∴ ∠1=∠ACD（等量代换），

∴ EF∥CD（同位角相等，两直线平行）.

∴ ∠AEF=∠ADC（两直线平行，同位角相等）.

∵ EF⊥AB（已知），∴ ∠AEF=90°（垂直的定义），

∴ ∠ADC=90°（等量代换）.

∴ CD⊥AB（垂直的定义）．

【点拨】利用垂直的定义除了由垂直得直角外，还能由直角判定垂直，判断两直线的夹角是否为90°是判断两直线是否垂直的基本方法．

类型三、命题及平移

4.下列命题中真命题是（ ）

A．若a2=b2,则a=b B．4的平方根是±2

C．两个锐角之和一定是钝角 D．相等的两个角是对顶角

【答案】B

【分析】利用对顶角的性质、平方根的性质、锐角和钝角的定义分别判断后即可确定正确的选项．

解：A、若a2=b2,则a=±b，错误，是假命题；

B、4的平方根是±2，正确，是真命题；

C、两个锐角的和不一定是钝角，故错误，是假命题；

D、相等的两个角不一定是对顶角，故错误，是假命题.

故选B．

【点拨】考查了命题与定理的知识，解题的关键是了解对顶角的性质、平方根的性质、锐角和钝角的定义，难度不大．

举一反三：

【变式】把命题“如果x=y，那么=”作为原命题，对原命题和它的逆命题的真假性的判断，下列说法正确的是（　　）

A．原命题和逆命题都是真命题 B．原命题和逆命题都是假命题

C．原命题是真命题，逆命题是假命题 D．原命题是假命题，逆命题是真命题

【答案】D

【分析】写出该命题的逆命题，结合“算术平方根的意义”分别判断出原命题和逆命题的真假性即可确定四个选项中说法的正误了.

解：∵命题“如果，则”在“是负数时，不成立”，

∴原命题是假命题；

∵命题“如果，则”的逆命题“若，则”是真命题，

∴该题中，原命题的逆命题是真命题.

即在该题中，“原命题”是假命题，“逆命题”是 真命题.

故选D.

【点拨】能由“原命题”写出“逆命题”并结合“算术平方根的意义”判断出命题的真假，是解答本题的关键.

5.如图，将△ABC沿着点B到C的方向平移到△DEF的位置，AB=10，DO=4，平移距离为6，则阴影部分面积为（   ）

A．42 B．96 C．84 D．48

【答案】D

解：由平移的性质知，BE=6，DE=AB=10，

∴OE=DE﹣DO=10﹣4=6，

∴S四边形ODFC=S梯形ABEO=（AB+OE）•BE=（10+6）×6=48．

故选D.

【点拨】本题考查平移的性质，平移前后两个图形大小，形状完全相同，图形上的每个点都平移了相同的距离，对应点之间的距离就是平移的距离.

举一反三：

【变式】如图：在正方形网格中有一个，按要求进行下列作图（只能借助于网格）．

（1）画出先将向右平移6格．再向上平移3格后的（点A平移到点D．点B平移到点E）．

（2）连接，那么与的关系是__________，线段所组成的封闭图形的面积为__________．

【答案】（1）见解析；（2）AD∥BE，AD=BE，9

【分析】（1）根据平移的性质，画出图形即可．

（2）利用平移的性质判断即可，利用平行四边形的面积公式计算即可．

解：（1）如图，△DEF即为所求．

（2）由平移的性质可知，AD∥BE，AD=BE．

线段AB扫过的部分所组成的封闭图形的面积=3×3=9．

故答案为：AD∥BE，AD=BE，9．

【点拨】本题考查作图—平移变换，平移的性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考常考题型．

类型四、实际应用

6.如图，平原上有A，B，C，D四个村庄，为解决当地缺水问题，政府准备投资修建一个蓄水池．

（1）不考虑其他因素，请你画图确定蓄水池H点的位置，使它到四个村庄距离之和最小；

（2）计划把河水引入蓄水池H中，怎样开渠最短并说明根据．

 解答：本题考查了线段和垂线的性质在实际生活中的运用

（1）由两点之间线段最短可知，连接AD、BC交于H，则H为蓄水池位置；

（2）根据垂线段最短可知，要做一个垂直EF的线段．

⑴连结，，交于点，则为所求的蓄水池点．

⑵过作于，沿开挖，可使开挖的渠最短，依据是：“点与直线的连线中，垂线段最短”．（如图）

【变式】已知：∠1＝∠2，EG平分∠AEC．

（1）如图①，∠MAE＝45°，∠FEG＝15°，∠NCE＝75°．求证：AB∥CD；

（2）如图②，∠MAE＝140°，∠FEG＝30°，当∠NCE＝　   　°时，AB∥CD；

（3）如图②，请你直接写出∠MAE、∠FEG、∠NCE之间满足什么关系时，AB∥CD；

（4）如图③，请你直接写出∠MAE、∠FEG、∠NCE之间满足什么关系时，AB∥CD．

【答案】（1）见解析；（2）当∠NCE＝80°时，AB∥CD；（3）当2∠FEG+∠NCE＝∠MAE时AB∥CD；（4）当∠MAE+2∠FEG+∠NCE＝360°时，AB∥CD.

【分析】（1）由题意可得AB∥EF，根据平行线的性质，角平分线的性质可得角的数量关系，可求∠FEC=75°，即可求结论．

（2）由题意可得AB∥EF，根据平行线的性质，角平分线的性质可得角的数量关系，可求∠FEC=100°，再根据AB∥CD，可求∠NCE的度数

（3）由题意可得AB∥EF，根据平行线的性质，角平分线的性质可得角的数量关系，可求∠FEC=180°-∠MAE+2∠FEG，再根据AB∥CD，可求其关系．

（4）由题意可得AB∥EF，根据平行线的性质，角平分线的性质可得角的数量关系，可求∠FEC=∠MAE+2∠FEG-180°，再根据AB∥CD，可求其关系．

 证明（1）∵∠1＝∠2

∴AB∥EF

∴∠MAE＝∠AEF＝45°，且∠FEG＝15°

∴∠AEG＝60°

∵EG平分∠AEC

∴∠AEG＝∠CEG＝60°

∴∠CEF＝75°

∵∠ECN＝75°

∴∠FEC＝∠ECN

∴EF∥CD且AB∥EF

∴AB∥CD

（2）∵∠1＝∠2

∴AB∥EF

∴∠MAE+∠FEA＝180°且∠MAE＝140°

∴∠AEF＝40°

∵∠FEG＝30°

∴∠AEG＝70°

∵EG平分∠AEC

∴∠GEC＝∠AEG＝70°

∴∠FEC＝100°

∵AB∥CD，AB∥EF

∴EF∥CD

∴∠NCE+∠FEC＝180°

∴∠NCE＝80°

∴当∠NCE＝80°时，AB∥CD

（3）∵∠1＝∠2

∴AB∥EF

∴∠MAE+∠FEA＝180°

∴∠FEA＝180°﹣∠MAE，

∴∠AEG＝∠FEA+∠FEG＝180°﹣∠MAE+∠FEG

∵EG平分∠AEC

∴∠GEC＝∠AEG

∴∠FEC＝∠GEC+∠FEG＝180°﹣∠MAE+∠FEG+∠FEG＝180°﹣∠MAE+2∠FEG

∵AB∥CD，AB∥EF

∴EF∥CD

∴∠FEC+∠NCE＝180°

∴180°﹣∠MAE+2∠FEG+∠NCE＝180°

∴2∠FEG+∠NCE＝∠MAE

∴当2∠FEG+∠NCE＝∠MAE时AB∥CD

（4）∠1＝∠2

∴AB∥EF

∴∠MAE+∠FEA＝180°

∴∠FEA＝180°﹣∠MAE，

∴∠AEG＝∠FEG﹣∠FEA＝∠FEG﹣180°+∠MAE

∵EG平分∠AEC

∴∠GEC＝∠AEG

∴∠FEC＝∠FEA+2∠AEG＝180°﹣∠MAE+2∠FEG﹣360°+2∠MAE＝∠MAE+2∠FEG﹣180°

∵AB∥CD，AB∥EF

∴EF∥CD

∴∠FEC+∠NCE＝180°

∴∠MAE+2∠FEG﹣180°+∠NCE＝180°

∴∠MAE+2∠FEG+∠NCE＝360°

∴当∠MAE+2∠FEG+∠NCE＝360°时，AB∥CD

【点拨】本题考查了平行线的性质和判定，角平分线的性质，关键是由平行线的性质得到角的