

初中数学1.4平行线的性质图片ppt课件
展开平行线的性质(2) 学案
课题 | 平行线的性质(2) | 单元 | 第5单元 | 学科 | 数学 | 年级 | 七年级下册 |
学习 目标 | 1.知道两直线平行的断定方法,了解平行线的性质。 2.理解平行线的性质与判定方法,运用平行线的性质与判定解决一些问题。
| ||||||
重点 | 平行线的性质的灵活应用,发展推理能力。 | ||||||
难点 | 加深对平行线三条性质的理解,提高分析问题、解决问题的能力. | ||||||
教学过程 |
导入新课 | 【引入思考】
问题1 平行线的三条性质分别是什么? 性质1 两条平行线被第三条直线所截,同位角相等. 性质2 两条平行线被第三条直线所截,内错角相等. 性质3 两条平行线被第三条直线所截,同旁内角互补. 学习了平行线的性质后,我们能解决什么问题?
|
新知讲解 | 提炼概念 平行线的性质 平行线的判定 因为a∥b, 因为∠1=∠2, 所以∠1=∠2 所以a∥b. 因为a∥b, 因为∠2=∠3, 所以∠2=∠3, 所以a∥b. 因为a∥b, 因为∠2+∠4=180°, 所以∠2+∠4=180°, 所以a∥b.
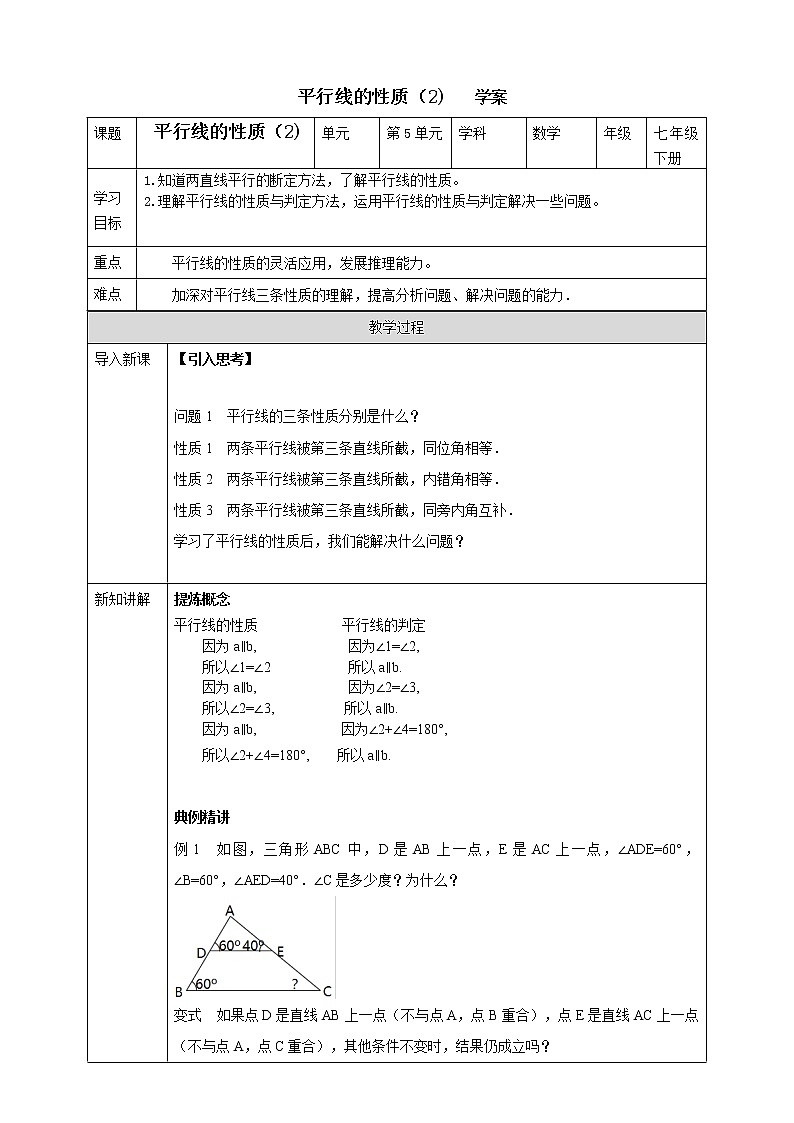
典例精讲 例1 如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠AED=40°.∠C是多少度?为什么? 变式 如果点D是直线AB上一点(不与点A,点B重合),点E是直线AC上一点(不与点A,点C重合),其他条件不变时,结果仍成立吗? (1)点D,E分别在线段AB ,AC的延长线上 (2)点D,E分别在线段BA ,CA的延长线上
例2 如图,EF∥AD,∠1=∠2,∠BAC=70 °,求∠AGD的度数. |
课堂练习 | 巩固训练 1.把一副三角板放在同一水平桌面上,摆放成如图所示的形状,使两个直角顶点重合,两条斜边平行,则∠1的度数是( ) A. 45° B. 60° C. 75° D. 82.5°
2.如图,点 E,F 分别在直线 AB,CD 上,点 G,H 在两直线之间,线段 EF 与 GH 相交于点 O,且有∠AEF + ∠CFE=180° ,∠AEF-∠1=∠2,则在图中相等的角共有( ) A.5对 B.6对 C.7对 D.8对
4.如图,MN,EF 表示两面互相平行的镜面,光线 AB 照射到镜面 MN 上,反射光线为 BC,此时∠1=∠2;光线 BC 经过镜面 EF 反射后的光线为 CD,此时∠3=∠4.试判断 AB 与 CD 的位置关系,并说明理由.
答案 引入思考
提炼概念
典例精讲 例1 解:∵∠ADE=60°,∠B=60°(已知), ∴∠ADE=∠B(等量代换). ∴DE∥BC(同位角相等,两直线平行). ∴∠C=∠AED(两直线平行,同位角相等). ∵∠AED=40°(已知), ∴∠C=40°(等量代换). 变式 如果点D是直线AB上一点(不与点A,点B重合),点E是直线AC上一点(不与点A,点C重合),其他条件不变时,结果仍成立吗? (1)点D,E分别在线段AB ,AC的延长线上
(2)点D,E分别在线段BA ,CA的延长线上
如果点D是直线AB上一点(不与点A,点B重合),点E是直线AC上一点(不与点A,点C重合),其他条件不变时,结果仍成立.
例2 解:∵EF∥AD(已知), ∴∠2=∠3.(两直线平行,同位角相等) ∵∠1=∠2(已知) ∴∠1=∠3.(等量代换) ∴DG∥AB.(内错角相等,两直线平行) ∴∠BAC+∠AGD=180°. (两直线平行,同旁内角互补) ∴∠AGD=180°-∠BAC=180°-70°=110°.
巩固训练 1.解析:如图,过点 E 作 EF//AB, ∵ AB//CD,∴ EF//CD, ∴ ∠AEF =∠A=45°,∠FEC =∠C =30°,∴ ∠1=∠AEF +∠FEC =45°+30°=75°.
2.解析:∵∠AEF+∠CFE=180°,∴AB//CD, ∴∠AEF =∠DFE,∠BEF=∠CFE. ∵ ∠AEF-∠1=∠2,∠AEF-∠1=∠AEG, ∴ ∠AEG=∠2. ∴ ∠1=∠EFH,∠BEG =∠CFH. ∴ GE//FH,∴ ∠G=∠H. 又∠EOG =∠FOH, ∠EOH=∠GOF, ∴ 图中相等的角共有 8 对. 3.解:在 PC 的另一侧作∠APE =∠BAP. ∴ EP∥AB. ∵AB∥CD,∴ EP∥CD. ∴∠EPC=∠PCD. ∵ ∠APE+∠APC=∠EPC, ∴ ∠APE+∠APC= ∠PCD, 即∠BAP+∠APC = ∠A+∠P =∠PCD. 4.解:AB//CD.理由如下: ∵ MN//EF(已知), ∴ ∠2=∠3(两直线平行,内错角相等). ∵ ∠1=∠2,∠3=∠4(已知), ∴ ∠1=∠2=∠3=∠4, ∴∠1+∠2=∠3+∠4. ∵ ∠ABC+∠1+∠2=180°, ∠BCD+∠3+∠4=180°(平角的性质), ∴ ∠ABC=∠BCD(等量代换). ∴ AB//CD(内错角相等,两直线平行).
|
课堂小结 | 小课堂小结 在解决问题时,我们可以这样进行思考: 已知、未知是什么?条件是什么? 能否借助条件让已知与未知产生联系? 以前是否解决过类似问题?能否类比进行求解?
在解决问题后,我们可以进行这样的反思: 这个问题的解决思路是什么?能用这种思路解决什么类型的问题? 在解决这个问题时,关键在哪里?自己是如何突破的? 改变问题中的部分条件,结果还成立吗? 得到的结论具有一般性吗?
|
初中数学浙教版七年级下册1.4平行线的性质评课ppt课件: 这是一份初中数学浙教版七年级下册1.4平行线的性质评课ppt课件,共25页。PPT课件主要包含了教材简析,三要素,两直线平行,动手画一画,学以致用,四谈收获,知识拓展等内容,欢迎下载使用。
初中数学浙教版七年级下册1.4平行线的性质课前预习课件ppt: 这是一份初中数学浙教版七年级下册1.4平行线的性质课前预习课件ppt,共6页。
浙教版七年级下册1.4平行线的性质图片课件ppt: 这是一份浙教版七年级下册1.4平行线的性质图片课件ppt,共21页。PPT课件主要包含了新知导入,情境引入,同位角,内错角,同旁内角,∵∠1∠2已知,∠3∠2已知,平行线的判定,合作学习,两直线平行等内容,欢迎下载使用。













