数学七年级下册1.3平行线的判定教课ppt课件

这是一份数学七年级下册1.3平行线的判定教课ppt课件，共18页。PPT课件主要包含了新知导入，情境引入，合作学习，提炼概念，合作探究，应用格式，典例精讲，典例精析，归纳概念，同位角等内容，欢迎下载使用。

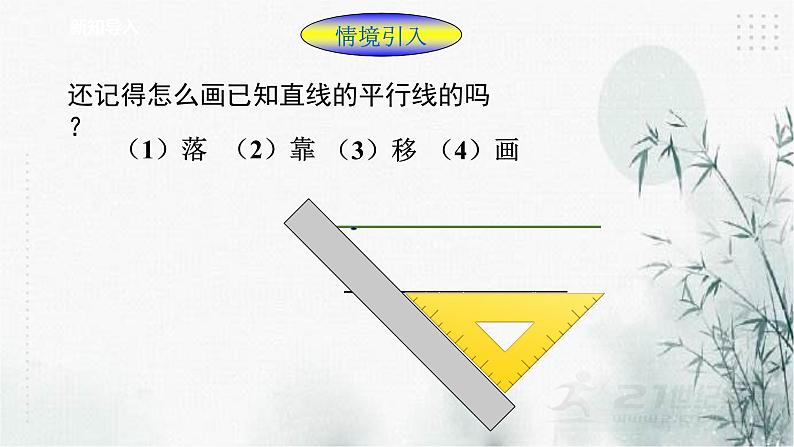
还记得怎么画已知直线的平行线的吗？
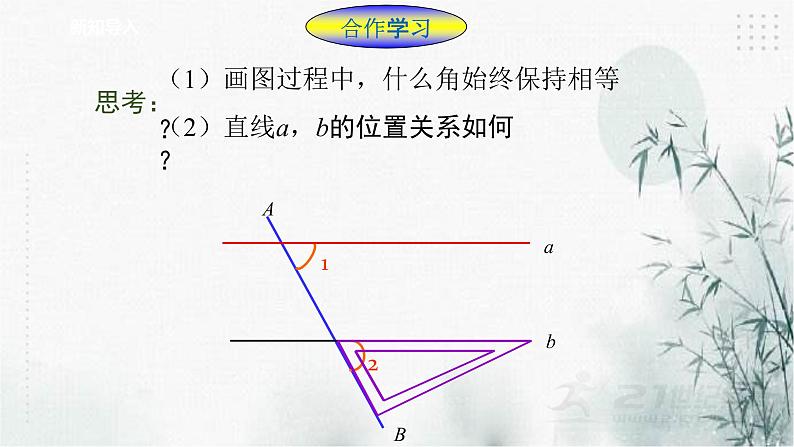
（1）画图过程中，什么角始终保持相等？
（2）直线a，b的位置关系如何？
判定方法1：两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
∵∠1=∠2(已知)，∴l1∥l2 （同位角相等，两直线平行）.
一、利用同位角判断两直线平行
解： ∵ 3=2(已知）， 1=3（对顶角相等），  1=2.  a//b(同位角相等，两直线平行）.
问题1：如图，由3=2，可推出a//b吗？如何推出的呢？
二、利用内错角和同旁内角判定两直线平行
判定方法2：两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.
∵∠3=∠2(已知)，∴a∥b（内错角相等，两直线平行）.
简单说成：内错角相等，两直线平行.
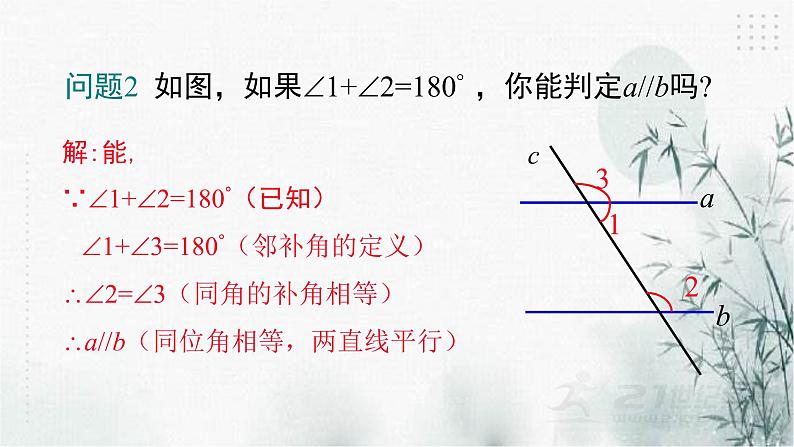
问题2 如图，如果1+2=180° ，你能判定a//b吗?
解:能, ∵1+2=180°（已知） 1+3=180°（邻补角的定义）2=3（同角的补角相等）a//b（同位角相等，两直线平行）
判定方法3：两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行.
简单说成：同旁内角互补，两直线平行.
∵∠1+∠2=180°(已知)，∴a∥b（同旁内角互补，两直线平行）.
已知条件：直线b与直线c都垂直于直线a.要说明的结论：直线b与直线c平行吗？
例1. 在同一平面内，如果两条直线都垂直于同一条直线，那么两条直线平行吗？为什么？
在同一平面内，垂直于同一条直线的两条直线平行．
判定两条直线平行的方法
1.如图，能判定EB∥AC的条件是(　　)A．∠C＝∠ABE B．∠A＝∠EBDC．∠C＝∠ABC D．∠C＝∠EBD
① ∵ ∠1 =_____ （已知） ∴ AB∥CE（ ）
② ∵ ∠2 = （已知） ∴ CD∥BF（ ）
③ ∵ ∠1 +∠5 =180（已知） ∴ _____∥_____( )
内错角相等，两直线平行
同位角相等,两直线平行
同旁内角互补,两直线平行
3．如图，要使AD∥BE，根据“内错角相等，两直线平行”必须满足_______________________条件(写出你认为正确的一个条件)．
∠1＝∠2或∠5＝∠D　
4 . 已知：如图，∠1=∠C，∠2=∠B，求证：MN∥EF.
∵ ∠1=∠C （已知）
∴ MN∥BC （内错角相等，两直线平行）
∵ ∠2=∠B （已知）
∴ EF∥BC （同位角相等，两直线平行）
∴ MN∥EF （平行于同一直线的两条直线平行）
5．如图，直线AB，CD分别与直线FE相交于点N，E，GE⊥FE与直线AB相交于点G，已知∠ANF＋∠DEG＝90°，请你说出AB∥CD的理由．
解：∵∠ANF＝∠ENG，∠ANF＋∠DEG＝90°，∴∠ENG＋∠DEG＝90°.∵GE⊥FE，∴∠NEG＝90°.∴∠ENG＋∠DEG＋∠NEG＝90°＋90°＝180°.∴∠ENG＋∠DEN＝180°.∴AB∥CD．