专题5.23 《相交线与平行线》动点问题（专项练习）-2021-2022学年七年级数学下册基础知识专项讲练（人教版）

这是一份专题5.23 《相交线与平行线》动点问题（专项练习）-2021-2022学年七年级数学下册基础知识专项讲练（人教版），共49页。试卷主要包含了综合与探究，已知， ， ．，如图1， 平分 ，已知等内容，欢迎下载使用。

专题5.23 《相交线与平行线》动点问题（专项练习）
1.（2020七下·温州期中）已知 ，点 是平面内的一个动点，连结 、PD
（1）如图一，当点 运动到 上方时，试说明： .

（2）如图二，当点 运动到 与 之间时，给出 的数量关系并说明理由.

（3）如图三，点 和点 是平面内的两个动点，连结 、 、 ，直接给出 的数量关系________.

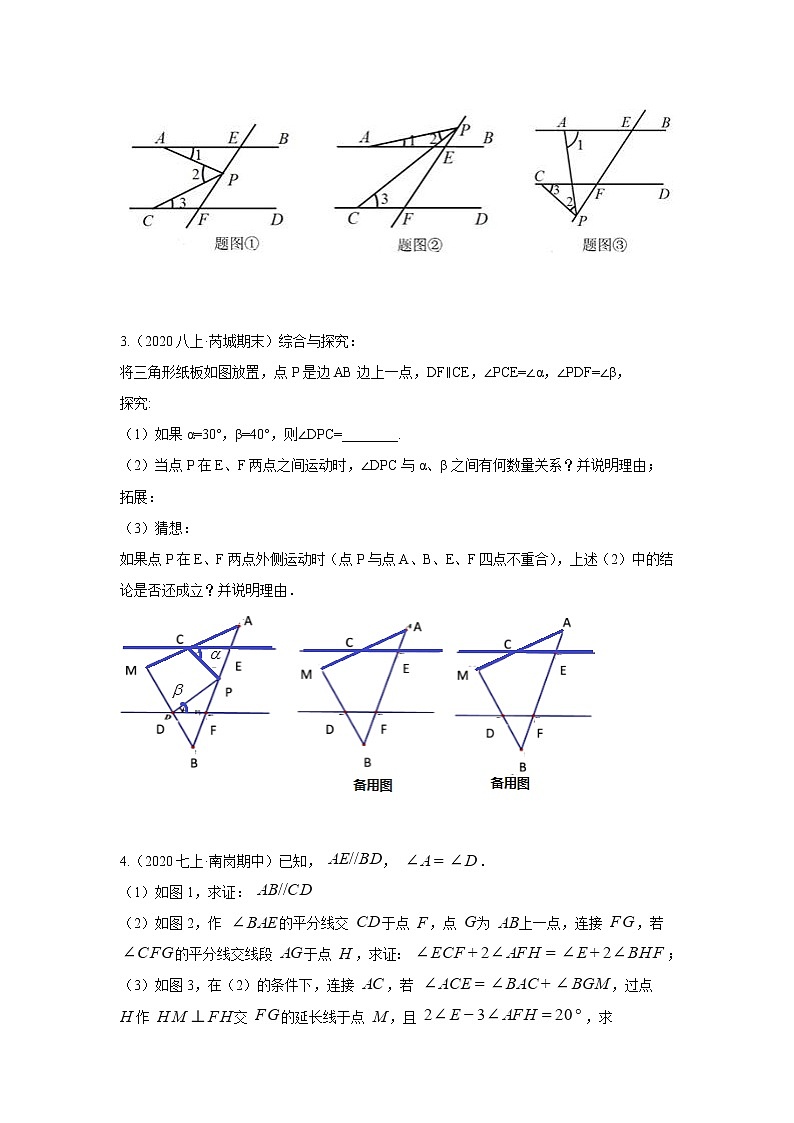
2.（2020七下·温州月考）已知直线AB平行CD，直线EF分别截AB、CD于点E、F两点。
（1）如图①，有一动点P在线段CD之间运动（不与C，D两点重合），试探究∠1、∠2、∠3的等量等关系？试说明理由。
（2）如图②、③，当动点P在线段CD之外运动（不与C，D两点重合），问上述结论是否还成立？若不成立，试写出新的结论并说明理由。



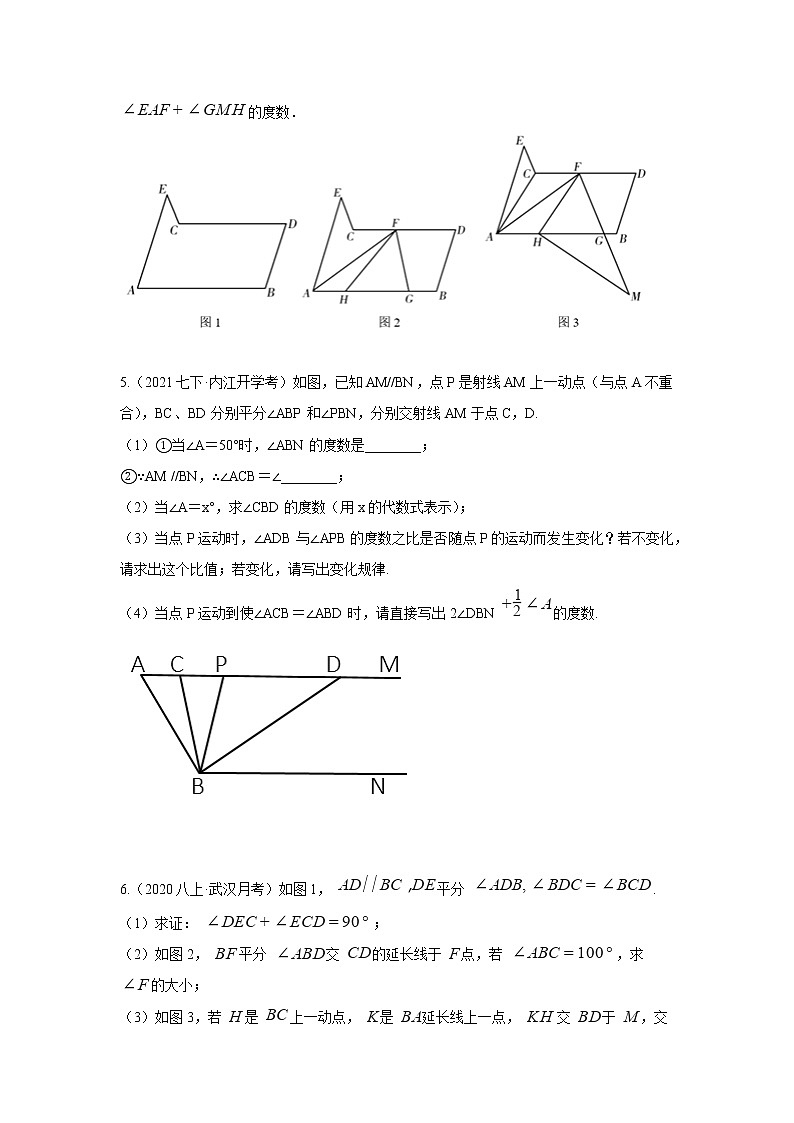
3.（2020八上·芮城期末）综合与探究：
将三角形纸板如图放置，点P是边AB边上一点，DF∥CE，∠PCE=∠α，∠PDF=∠β，
探究:
（1）如果α=30°，β=40°，则∠DPC=________.
（2）当点P在E、F两点之间运动时，∠DPC与α、β之间有何数量关系？并说明理由；
拓展：
（3）猜想：
如果点P在E、F两点外侧运动时（点P与点A、B、E、F四点不重合），上述（2）中的结论是否还成立？并说明理由．


4.（2020七上·南岗期中）已知， ， ．
（1）如图1，求证：
（2）如图2，作 的平分线交 于点 ，点 为 上一点，连接 ，若 的平分线交线段 于点 ，求证： ；
（3）如图3，在（2）的条件下，连接 ，若 ，过点 作 交 的延长线于点 ，且 ，求 的度数．


5.（2021七下·内江开学考）如图，已知AM//BN，点P是射线AM上一动点（与点A不重合），BC、BD分别平分∠ABP和∠PBN，分别交射线AM于点C，D.
（1）①当∠A＝50°时，∠ABN的度数是________；
②∵AM //BN，∴∠ACB＝∠________；
（2）当∠A＝x°，求∠CBD的度数（用x的代数式表示）；
（3）当点P运动时，∠ADB与∠APB的度数之比是否随点P的运动而发生变化？若不变化，请求出这个比值；若变化，请写出变化规律.
（4）当点P运动到使∠ACB＝∠ABD时，请直接写出2∠DBN 的度数.


6.（2020八上·武汉月考）如图1， 平分 .
（1）求证： ；
（2）如图2， 平分 交 的延长线于 点，若 ，求 的大小；
（3）如图3，若 是 上一动点， 是 延长线上一点， 交 于 ，交 于 平分 ,交 于 ，交 于 ，当 在线段 上运动时（不与 重合），求 .


7.（2020七下·新乡月考）如图1，CE平分∠ACD，AE平分∠BAC，∠EAC+∠ACE=90°.
（1）请判断AB与CD的位置关系，并说明理由；
（2）如图2，在（1）的结论下，当∠E=90°保持不变，移动直角顶点E，使∠MCE=∠ECD.当直角顶点E点移动时，问∠BAE与∠MCD是否存在确定的数量关系？并说明理由；
（3）如图3，在（1）的结论下，P为线段AC上一定点，点Q为直线CD上一动点，当点Q在射线CD上运动时（点C除外），∠CPQ+∠CQP与∠BAC有何数量关系？直接写出结论，其数量关系为________.




8.（2020七下·北京期末）如图，在三角形ABC中，点D是为BC上一点，连接 AD．
（1）三角形ABC中，∠BAC=90°，点E是AB上一点，过点E作EF//AD交BC于点F，作DG⊥AC于G．依题意补全图形，并判断∠BEF与∠ADG的数量关系，并加以证明．
（2）任意三角形ABC中，点E是AB延长线上一点，过点E作EF//AD交BC所在直线于点F，G是直线AC上一点，连接DG．若要使（1）结论仍成立，DG与AB位置关系应满足的条件?请画图并直接写出DG与AB位置关系．



9.（2019七下·合肥期末）已知：三角形ABC和同一平面内的点D．
（1）如图1，点D在BC边上，DE∥BA交AC于E，DF∥CA交AB于F．若∠EDF=85°，则∠A的度数为________°．
（2）如图2，点D在BC的延长线上，DF∥CA，∠EDF=∠A，证明：DE∥BA．
（3）如图3，点D是三角形ABC外部的一个动点，过D作DE∥BA交直线AC于E，DF∥CA交直线AB于F，直接写出∠EDF与∠A的数量关系（不需证明）．

10.（2020七上·南岗期末）已知：直线 分别与直线 ， 相交于点 ， ，并且
（1）如图1，求证： ；

（2）如图2，点 在直线 ， 之间，连接 ， ，求证： ；

（3）如图3，在（2）的条件下，射线 是 的平分线，在 的延长线上取点 ，连接 ，若 ， ，求 的度数．


11. （2020七下·高港期中）如图
（1）问题情境：如图1，AB∥CD，∠PAB=135°，∠PCD=125°.求∠APC度数.小明的思路是：如图2，过P作PE∥AB，通过平行线性质，可求得∠APC的度数.请写出具体求解过程.
（2）问题迁移：如图3，AD∥BC，点P在射线OM上运动，当点P在A、B两点之间运动时，∠ADP=∠α，∠BCP=∠β.∠CPD、∠α、∠β之间有何数量关系？请说明理由；

（3）在(1)的条件下，如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合)，请你直接写出∠CPD、∠α、∠β间的数量关系.

12.（2020七下·太原期中）课题学习：平行线的“等角转化功能.
（1）问题情景：如图1，已知点 是 外一点，连接 、 ，求 的度数.
天天同学看过图形后立即想出： ，请你补全他的推理过程.
解：（1）如图1，过点 作 ，∴ ________， ________.
又∵ ，∴ .
解题反思：从上面的推理过程中，我们发现平行线具有“等角转化”功能，将 ， ， “凑”在一起，得出角之间的关系，使问题得以解决.
（2）问题迁移：如图2， ，求 的度数.
（3）方法运用：如图3， ，点 在 的右侧， ，点 在 的左侧， ， 平分 ， 平分 ， 、 所在的直线交于点 ，点 在 与 两条平行线之间，求 的度数.
                
13.（2019七下·茂名期中）如图1，CE平分∠ACD，AE平分∠BAC，∠EAC+∠ACE=90°
（1）请判断AB与CD的位置关系并说明理由；
（2）如图2，当∠E=90°且AB与CD的位置关系保持不变，移动直角顶点E，使∠MCE=∠ECD，当直角顶点E点移动时，问∠BAE与∠MCD否存在确定的数量关系？并说明理由；
（3）如图3，P为线段AC上一定点，点Q为直线CD上一动点且AB与CD的位置关系保持不变，当点Q在射线CD上运动时（点C除外）∠CPQ+∠CQP与∠BAC有何数量关系？猜想结论并说明理由．

14.（2020七下·德州月考）如图，已知直线l1∥l2 ， 且l3和l1 ， l2分别交于A，B两点，点P在AB上. ．
（1）试找出∠1，∠2，∠3之间的关系并说出理由；
（2）如果点P在A，B两点之间运动，问∠1，∠2，∠3之间的关系是否发生变化；
（3）如果点P在A，B两点外侧运动，试探究∠1，∠2，∠3之间的关系（点P和A，B不重合） ．

15.（2020七下·锡山期末）如图1，已知直线MN GH，且MN和GH之间的距离为1，小明同学制作了两个直角三角形硬纸板ACB和DEF，其中∠ACB=90°，∠DFE=90°，∠BAC=45°，∠EDF=30°，AC=1.小明利用这两块三角板进行了如下的操作探究：
（1）如图1，点A在MN上，边BC在GH上，边DE在直线AB上.
①将直角三角形DEF沿射线BA的方向平移，当点F在MN上时，如图2，求∠AFE的度数；
②将直角三角形DEF从图2的位置继续沿射线BA的方向平移，当以A、D、F为顶点的三角形是直角三角形时，求∠FAN度数；
（2） 将直角三角形ABC如图3放置，若点A在直线MN上，点C在MN和GH之间（不含MN，GH上），边BC和AB与直线GH分别交于D，K.在△ABC绕着点A旋转的过程中，设∠MAK=n°，∠CDK=(4m﹣2n﹣10)°，则m的取值范围为________.

16.（2020七下·阜阳期中）如图 ，已知直线l1 ， l2 ， 点P在直线l3上且不与点A、B重合．记∠AEP=∠1，∠BFP=∠2，∠EPF=∠3．
（1）如图 ，若直线l1//l2 ， 点P在线段AB（A、B两点除外）上运动时，写出∠1、∠2、∠3之间的关系，并说明理由．
（2）如图 ，若（1）中∠1、∠2、∠3之间的关系成立，你能不能反向推出直线l1//l2？若成立请说明理由．
（3）如图 ，若直线l1//l2 ， 若点P在A、B两点外侧运动时（不包括线段AB），请直接写出∠1、∠2、∠3之间的关系．

17.（2020七下·厦门期末）如图，以直角△AOC的直角顶点O为原点，以OC，OA所在直线为x轴和y轴建立平面直角坐标系，点A（0，a），C（b，0）满足 ．
（1）点A的坐标为________；点C的坐标为________．
（2）已知坐标轴上有两动点P，Q同时出发，P点从C点出发沿x轴负方向以每秒2个单位长度的速度匀速移动，Q点从O点出发沿y轴正方向以每秒1个单位长度的速度匀速移动，点P到达O点整个运动随之结束．AC的中点D的坐标是（4，3），设运动时间为t秒．问：是否存在这样的t，使得△ODP与△ODQ的面积相等？若存在，请求出t的值；若不存在，请说明理由．
（3）在（2）的条件下，若∠DOC=∠DCO，点G是第二象限中一点，并且y轴平分∠GOD．点E是线段OA上一动点，连接接CE交OD于点H，当点E在线段OA上运动的过程中，探究∠GOA，∠OHC，∠ACE之间的数量关系，并证明你的结论（三角形的内角和为180°可以直接使用）．


18.（2020七下·桦南期中）根据下图回答问题：
（1）如图1，CM平分∠ACD，AM平分∠BAC，∠MAC+∠ACM=90°，请判断AB与CD的位置关系并说明理由；
（2）如图2，当∠M=90°且AB与CD的位置关系保持（1）中的不变，当直角顶点M移动时，问∠BAM与∠MCD是否存在确定的数量关系？并说明理由；
（3）如图3，G为线段AC上一定点，点H为直线CD上一动点且AB与CD的位置关系保持（1）中的不变，当点H在射线CD上运动时（点C除外）∠CGH+∠CHG与∠BAC有何数量关系？猜想结论并说明理由．


19.（2020七下·青岛期中）已知直线l1∥l2 ， 且l4和l1、l2分别交于A、B两点，点P为线段AB上的一个定点（如图1）

（1）写出∠1、∠2、∠3、之间的关系并说出理由．
（2）如果点P为线段AB上．的动点时，问∠1、∠2、∠3之间的关系是否发生变化？（不必说理由）
（3）如果点P在A、B两点外侧运动时， （点P和点A、点B不重合）

①如图2，当点P在射线AB上运动时，∠1、∠2、∠3之间关系并说出理由．
②如图3，当点P在射线BA上运动时，∠1、∠2、∠3之间关系（不说理由）
20.（2020七下·北京月考）问题情境：如图1， ， ， ．求 度数．
小明的思路是：如图2，过 作 ，通过平行线性质，可得 ．
问题迁移：
（1）如图3， ，点 在射线 上运动，当点 在 、 两点之间运动时， ， ． 、 、 之间有何数量关系?请说明理由；
（2）在（1）的条件下，如果点 在 、 两点外侧运动时（点 与点 、 、 三点不重合），请你直接写出 、 、 间的数量关系．



21.（2020七下·莆田月考）如图 1，CE 平分∠ACD，AE 平分∠BAC，且∠EAC＋∠ACE=90°．
（1）请判断 AB 与 CD 的位置关系，并说明理由；
（2）如图 2，若∠E=90°且 AB 与 CD 的位置关系保持不变，当直角顶点 E 移动时，写出∠BAE 与∠ECD 的数量关系，并说明理由；
（3）如图 3，P 为线段 AC 上一定点，点 Q 为直线 CD 上一动点，且 AB 与 CD 的位置 关系保持不变，当点 Q 在射线 CD 上运动时(不与点 C 重合)，∠PQD，∠APQ 与∠ BAC 有何数量关系？写出结论，并说明理由．

22.（2020七下·孝南期末）如图 ，在平面直角坐标系中，线段 的两个端点分别为 ， ，将线段 向右平移3个单位长度，得到线段 ，连接

（1）直接写出点 、点 的坐标
（2）如图 ，延长 交 轴于点 ，点 是线段 上的一动点，连接 、 ，猜想 、 、 之间的数量关系，并说明理由
（3）在 轴上是否存在点 ，使 的面积与四边形 的面积相等，若存在，求出 的坐标，若不存在，请说明理由

23.（2020七上·南召期末）问题情景：如图1，AB∥CD，∠PAB=130°，∠PCD=120°，求∠APC的度数．
（1）数学活动小组经过讨论形成下列推理，请你补全推理依据．
如图2，过点P作PE∥AB，
∵PE∥AB(作图知)
又∵AB∥CD，
∴PE∥CD．________
∴∠A+∠APE=180°．
∠C+∠CPE=180°．________
∵∠PAB=130°，∠PCD=120°，
∴∠APE=50°，∠CPE=60°
∴∠APC=∠APE+∠CPE=110°．
（2）如图3，AD∥BC，当点P在A、B两点之间运动时，∠ADP=α，∠BCP=β，求∠CPD与α、β之间有何数量关系？请说明理由．
（3）在（2）的条件下，如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请你直接写出∠CPD与α、β之间的数量关系．

参考答案
一、综合题
1.【答案】 （1）略
（2）
（3）
【考点】平行线的判定与性质
【解析】【解析】解：（1）如图：延长AB交PD于点E，


∵AB∥CD，∴∠D=∠AEP，∵∠A+∠P+∠AEP=180°，∴ ；
（2）∠P-∠D+∠A=180°,理由如下：
如图，过点P作PE∥AB，

∵AB∥CD，AB∥PE，∴PE∥CD，∠A+∠APE=180°，∠D=∠DPE，∴∠APE=∠APD-∠DPE=∠APD-∠D，∴∠A+∠APD-∠D=180°，即∠P-∠D+∠A=180°；
（3）∠P-∠A=∠Q-∠D，理由如下：
如图：过点P作PE∥AB，过点Q作QF∥AB，

∵PE∥AB，QF∥AB，AB∥CD，∴AB∥PE∥QF∥CD，∴∠A=∠APE，∠EPQ=∠PQF，∠FQD=∠D，∵∠EPQ=∠APQ-∠APE，∠PQF=∠PQD-∠FQD，∴∠APQ-∠APE=∠PQD-∠FQD，∴∠APQ-∠A=∠PQD-∠D，即∠P-∠A=∠Q-∠D.
故答案为：∠P-∠A=∠Q-∠D.
【分析】（1）如图一：延长AB交PD于点E，根据二直线平行，同位角相等得出∠D=∠AEP，进而根据三角形的内角和定理即可得出结论；
（2）∠P-∠D+∠A=180°,理由如下：如图二，过点P作PE∥AB，根据平行于同一直线的两条直线互相平行得出PE∥CD，根据二直线平行同旁内角互补得出∠A+∠APE=180°，根据二直线平行，内错角相等得出∠D=∠DPE，进而根据角的和差及等量代换即可得出结论；
（3）∠P-∠A=∠Q-∠D，理由如下：如图三：过点P作PE∥AB，过点Q作QF∥AB，根据平行于同一直线的两条直线互相平行得出AB∥PE∥QF∥CD，根据二直线平行，内错角相等得出∠A=∠APE，∠EPQ=∠PQF，∠FQD=∠D，进而根据角的和差及等量代换即可得出结论.
2.【答案】 （1）解：∠2=∠1+∠3理由如下：
如图，过点P作PQ∥AB，则∠1=∠APQ.

∵AB∥CD，PQ∥AB，
∴PQ∥CD.
∴∠3=∠CPQ.
∵∠2=∠APQ+∠CPQ
=∠1+∠3.

（2）解：解：②∠2=∠1+∠3不成立，新的结论为∠2=∠3 ∠1.理由如下：
如图，过点P作PQ∥AB，则∠1=∠APQ.

∵AB∥CD，PQ∥AB，
∴PQ∥CD.
∴∠3=∠CPQ.
∠2=∠CPQ ∠APQ
=∠3 ∠1.
③∠2=∠1+∠3不成立，新的结论为∠2=∠1 ∠3.理由如下：
如图，过点P作PQ∥AB，则∠1=∠APQ.

∵AB∥CD，PQ∥AB，
∴PQ∥CD.
∴∠3=∠CPQ.
∠2=∠APQ ∠CPQ
=∠1 ∠3.
综合②、③的结论，∠2= .
【考点】角的运算，平行线的判定与性质
【解析】【分析】（1）∠2=∠1+∠3，理由如下：如图，过点P作PQ∥AB，利用平行线的判定与性质可得∠1=∠APQ，PQ∥CD∥AB，利用平行线的性质可得∠3=∠CPQ，由∠2=∠APQ+∠CPQ即得结论；
（2）不成立，新的结论为∠2=∠3  ∠1.理由：如图，过点P作PQ∥AB，利用平行线的判定与性质可得∠1=∠APQ，PQ∥CD∥AB，利用平行线的性质可得∠3=∠CPQ， 由∠2=∠CPQ  ∠APQ即可求出结论；
（3）不成立，新的结论为∠2=∠1  ∠3.理由如下： 同（1）可证∠1=∠APQ，∠3=∠CPQ，利用 ∠2=∠APQ  ∠CPQ 即可求出结论.
3.【答案】 （1）70°
（2）∠DPC=α+β，理由是：
如图，过P点作GH∥DF，

∵DF∥CE
∴GH∥CE
∴∠PCE=∠CPG=α，∠PDF=∠GPD=β
∵∠DPC=∠CPG+∠GPD=α+β

（3）（2）中的结论不成立，理由是：
如图，过P作PH∥DF

（图1）
∵DF∥CE
∴PH∥CE
∴∠PCE=∠1=α
∵∠FDP=∠2=β
∵∠DPC=∠FDP-∠PCE=∠2-∠1=β -α.
如图2，过P作PH∥DF

（ 图2）
∵DF∥CE
∴PH∥CE
∴∠PCE=∠1=α
∵∠FDP=∠2=β
∵∠DPC=∠PCE-∠FDP=∠1-∠2=α -β.
故（2）中的结论不成立.
【考点】角的运算，平行线的性质，三角形-动点问题
【解析】【解答】（1）过P点作GH∥DF，

∵DF∥CE,
∴GH∥CE
∴∠PCE=∠CPG=α，∠PDF=∠GPD=β
∵∠DPC=∠CPG+∠GPD =α+β
∵α=30°，β=40°
∴∠DPC=70°
故答案为：70°
【分析】（1）过P点作GH∥DF，可得GH∥CE，根据“两直线平行，内错角相等” 解答即可；（2）过P点作GH∥DF，可得GH∥CE，根据“两直线平行，内错角相等” 解答即可；（3）过P点作PH∥DF，可得PH∥CE，分P点在直线CE上方、DF下方两种情况，根据“两直线平行，内错角相等” 解答即可；
4.【答案】 （1）证明：∵ ，
∴ ，
又∵ ，
∴ ，
∴

（2）解：过 作 ，

∵ ，
∴ ，
∴ ， ．
又∵ ，
∴ ，
即 ．
∵ 平分 ，
∴ ．
∵ 平分 ，
∴ ．
∵ ，
∴ ， ，
设 ， ，
∵ ，
∴ ， ，
∴

，
∴ ；

（3）解：延长 至点 ，

∵ ，
∴ ， ， ， ．
又∵ ，
∴ ，
∴ ．
又∵ ， ，
∴ ，
由（2）问知， ，
，
∴ ．
又∵ ，
∴ ，
由（2）问知， ， ，
∵ ，
∴ ，
∴ ，
过 作 ，
∴ ，
∴ ，
，
∴ ，
由（2）问知， ，
∴ ，
∴ ，
∴ ．
【考点】平行线的判定与性质，角平分线的定义
【解析】【分析】（1）由AE∥BD，可得∠A+∠B=180°，由∠A=∠D得出∠B+∠D=180°，根据同旁内角互补两直线平行即证；
（2）过作， 设， ， 根据角平分线的定义、平行线的性质及交的和差关系可证结论；
（3）延长  至点 ， 根据平行线的性质及等量代换，可得 ，由补角的性质得出， 结合（2）可求出∠AFH=20°， 过  作   ，  可证  ，从而求出．
5.【答案】 （1）130°；CBN
（2）解：∵AM∥BN，
∴∠ABN＋∠A=180°，
∴∠ABN=180°-x°，
∴∠ABP＋∠PBN=180°-x°，
∵BC平分∠ABP，BD平分∠PBN，
∴∠ABP=2∠CBP，∠PBN=2∠DBP，
∴2∠CBP＋2∠DBP=180°-x°，
∴∠CBD=∠CBP＋∠DBP= ；

（3）解：不变，∠APB:∠ADB=2:1，
∵AM∥BN，
∴∠APB=∠PBN，∠ADB=∠DBN，
∵BD平分∠PBN，
∴∠PBN=2∠DBN，
∴∠APB:∠ADB=2:1；

（4）解：∵AM∥BN，
∴∠ACB=∠CBN，
当∠ACB=∠ABD时，则有∠CBN=∠ABD，
∴∠ABC＋∠CBD=∠CBD＋∠DBN，
∴∠ABC=∠DBN，
∴∠ABC=∠DBN=∠CBP=∠DBP，
∴2∠DBN= ∠ABN，
∵∠A+∠ABN=180°，
∴2∠DBN+ ∠A= （∠A+∠ABN）=90°.
【考点】平行线的性质，角平分线的定义
【解析】【解答】（1）解：①∵AM∥BN，∠A=50°，
∴∠ABN=180°-∠A=130°，
故答案为：130°；
②∵AM∥BN，
∴∠ACB=∠CBN，
故答案为：CBN
【分析】（1）①利用平行线的性质求出∠ABN的度数；②利用两直线平行，内错角相等，可证得结论.
（2）利用平行线的性质，可证得∠ABN＋∠A=180°，由此可推出∠ABP＋∠PBN=180°-x°，再利用角平分线的定义可证得∠ABP=2∠CBP，∠PBN=2∠DBP，可推出2∠CBP＋2∠DBP=180°-x°，从而可表示出∠CBD.
（3）利用平行线的性质，可证得∠APB=∠PBN，∠ADB=∠DBN，利用角平分线的定义，可得到∠PBN=2∠DBN；然后求出∠APB:∠ADB的比值.
（4）利用平行线的性质，可证得∠ACB=∠CBN，利用已知条件，推出∠CBN=∠ABD；再证明∠ABC=∠DBN=∠CBP=∠DBP，可求出2∠DBN= ∠ABN，∠A+∠ABN=180°；然后代入计算可求出2∠DBN 的度数.
6.【答案】 （1）证明：∵AD∥BC，
∴∠ADC+∠BCD=180°，
∵DE平分∠ADB，
∴∠EDB=∠EDA，
∴∠ADC+∠BCD=∠EDB+∠EDA+∠BDC+∠BCD=2（∠EDB+∠BDC）=180°，
∴∠EDB+∠BDC=90°，
∴∠DEC+∠ECD=180°-∠EDC=90°

（2）解：设∠ABF=x，
∵ 平分 ，
∴∠DBF=∠ABF=x，
∴∠DBC=∠ABC-∠DBF-∠ABF=100°-2x，
∵∠BDC=∠BCD，
∴∠ ，
∴∠F=∠BDC-∠DBF=40°+x-x=40°

（3）解：设AD交KG于P，

∵ 平分 ，DE平分∠ADB，
∴∠BKH=2∠NKH，∠ADB=2∠ADE，
∴∠BAD+∠DMH=∠BKH+∠AOK+∠ADB+∠DOM=2∠NKH+2∠AOK+2∠ADE=2（∠NKH+∠AOK+∠ADE）=2（∠NPD+∠ADE）=2∠DNG，
∴ =2.
【考点】平行线的性质，三角形内角和定理，三角形的外角性质，角平分线的定义
【解析】【分析】（1）根据两直线平行同旁内角互补得出 ∠ADC+∠BCD=180°， 进而根据角平分线的定义及等量代换得出 ∠EDB+∠BDC=90°，最后根据三角形的内角和定理即可得出 ；
（2）根据题意设∠ABF=x，利用角平分线的定义得出 ∠DBF=∠ABF=x， 根据角的和差得出 ∠DBC=100°-2x， 接着利用三角形的内角和定理得出∠BDC=40°+x，最后根据三角形的外角性质，由 ∠F=∠BDC-∠DBF 算出答案；
（3）根据题意设AD交KG于P，进而结合角平分线的性质得出 ∠BKH=2∠NKH，∠ADB=2∠ADE， 然后得出 ∠BAD+∠DMH=∠BKH+∠AOK+∠ADB+∠DOM=2∠NKH+2∠AOK+2∠ADE=2（∠NKH+∠AOK+∠ADE）=2（∠NPD+∠ADE）=2∠DNG， 从而即可得出答案.
7.【答案】 （1）解：AB∥CD；理由如下：
∵CE平分∠ACD，AE平分∠BAC，
∴∠BAC＝2∠EAC，∠ACD＝2∠ACE，
∵∠EAC＋∠ACE＝90°，
∴∠BAC＋∠ACD＝180°，
∴AB∥CD

（2）解：∠BAE＋ ∠MCD＝90°；理由如下：
过E作EF∥AB，如图2所示：

∵AB∥CD，
∴EF∥AB∥CD，
∴∠BAE＝∠AEF，∠FEC＝∠DCE，
∵∠AEC＝90°，
∴∠BAE＋∠ECD＝90°，
∵∠MCE＝∠ECD
∴∠ECD＝ ∠MCD
∴∠BAE＋ ∠MCD＝90°

（3）∠BAC＝∠CPQ＋∠CQP
【考点】平行线的判定与性质，三角形内角和定理，角平分线的定义
【解析】【解答】解：（3）∠BAC＝∠CPQ＋∠CQP；理由如下：
∵AB∥CD，
∴∠BAC＋∠ACD＝180°，
∵∠CPQ＋∠CQP＋∠PCQ＝180°，
即（∠CPQ＋∠CQP）＋∠ACD＝180°，
∴∠BAC＝∠CPQ＋∠CQP.
故答案为：∠BAC＝∠CPQ＋∠CQP.
【分析】（1）由角平分线的性质得出∠BAC＝2∠EAC，∠ACD＝2∠ACE，推出∠BAC＋∠ACD＝180°，即可得出结论；
（2）过E作EF∥AB，则EF∥AB∥CD，得出∠BAE＝∠AEF，∠FEC＝∠DCE，由∠AEC＝90°，推出∠BAE＋∠ECD＝90°，∠ECD＝ ∠MCD，得出∠BAE＋ ∠MCD＝90°；
（3）由平行线的性质得出∠BAC＋∠ACD＝180°，由三角形内角和定理得出∠CPQ＋∠CQP＋∠PCQ＝180°，即可得出结果.
8.【答案】 （1）解：如图所示，

∠BEF与∠ADG的数量关系是：∠BEF=∠ADG
证明：∵EF//AD，
∴∠BEF=∠BAD，
∵∠BAC=90°，即∠BAD+∠DAC=90°，
∴∠BEF+∠DAC=90°
∵DG⊥AC，
∴∠DAG+∠ADG=90°，
∴∠BEF=∠ADG；

（2）当DG与AB平行时，（1）中的结论仍然成立
【考点】垂线，平行线的性质
【解析】【解答】解：（2）如图所示，

∵EF//AD
∴∠AEF=∠BAD，
∵DG//AB，
∴∠BAD=∠ADG，
∴∠AEF=∠ADG，
故当DG与AB平行时，（1）中的结论仍然成立．
【分析】（1）根据题意画出图形即可，根据EF//AD可得∠BEF=∠BAD，由DG⊥AC得∠DAG+∠ADG=90°，再由∠BAD+∠DAG=90°可得结论；（2）由EF//AD可得∠AEF=∠BAD，由DG//AB可得∠BAD=∠ADG，进一步可得结论．
9.【答案】 （1）85
（2）证明：如图1，延长BA交DF于G．

∵DF∥CA，
∴∠2=∠3．
又∵∠1=∠2，
∴∠1=∠3．
∴DE∥BA．

（3）∠EDF+∠A=180°
【考点】平行线的判定与性质
【解析】【解答】（1）∵DE∥BA，DF∥CA，

∴∠A=∠DEC，∠DEC=∠EDF，
∵∠EDF=85°
∴∠A=∠EDF=85°；
故答案为：85；（3）∠EDF=∠A，∠EDF+∠A=180°，
理由：如图2，∵DE∥BA，DF∥CA，
∴∠EDF+∠E=180°，∠E+∠EAF=180°，
∴∠EDF=∠EAF=∠A；
如图3，∵DE∥BA，DF∥CA，

∴∠EDF+∠F=180°，∠F=∠CAB，
∴∠EDF+∠BAC=180°．
即∠EDF+∠A=180°
【分析】（1）根据平行线的性质，即可得到∠A=∠EDF=85°；（2）延长BA交DF于G．根据平行线的性质以及判定进行推导即可；（3）分两种情况讨论，即可得到∠EDF与∠A的数量关系：∠EDF=∠A，∠EDF+∠A=180°．
10.【答案】 （1）解：证明：如图，
 
∵ ， ．
∴ ，
∴ ．

（2）解：证明：如图，过点 作 ，
 
又∵ ，
∴ ．
∴ ， ．
∴

（3）解：解：如图，

令 ， ，
∵
则 ， ，
∵射线 是 的平分线，
∴ ，
∴ ，
∵ ，
∴ ，
∴ ，
过点 作 ，则 ， ，
∴ ，
∴ ，
∵ ，
∴ ，
∴ ，
∴ ，
∴ ．
【考点】平行线的判定与性质
【解析】【分析】（1）先求出 ，即可作答；
（2）先证明 ，再求出   ，    ，即可作答；
（3）根据平行线的性质和角平分线的性质进行求解即可。
11.【答案】 （1）解：过P作PE∥AB，


∵AB∥CD，
∴PE∥AB∥CD，
∴∠APE=180°-∠PAB=180°-135 =45°，
∠CPE=180°-∠PCD=180°-125 =55°，
∴∠APC=45°+55°=100°，

（2）解：∠CPD=∠α+∠β，理由如下：
如图3，过P作PE∥AD交CD于E，
∵AD∥BC，
∴AD∥PE∥BC，
∴∠α=∠DPE，∠β=∠CPE，
∴∠CPD=∠DPE+∠CPE=∠α+∠β；

（3）解：当P在BA延长线时，∠CPD=∠β-∠α；
理由：如图4，过P作PE∥AD交CD于E，

∵AD∥BC，
∴AD∥PE∥BC，
∴∠α=∠DPE，∠β=∠CPE，
∴∠CPD=∠CPE-∠DPE=∠β-∠α；
当P在BO之间时，∠CPD=∠α-∠β.
理由：如图5，过P作PE∥AD交CD于E，

∵AD∥BC，
∴AD∥PE∥BC，
∴∠α=∠DPE，∠β=∠CPE，
∴∠CPD=∠DPE-∠CPE=∠α-∠β.
【考点】平行线的判定与性质
【解析】【分析】问题情境：过P作PE∥AB，构造同旁内角，通过平行线性质，可得∠APC=45°+55°=100°；
问题迁移：(1)过P作PE∥AD交CD于E，推出AD∥PE∥BC，根据平行线的性质得出∠α=∠DPE，∠β=∠CPE，即可得出答案；(2)画出图形(分两种情况：①点P在BA的延长线上，②点P在AB的延长线上)，根据平行线的性质得出∠α=∠DPE，∠β=∠CPE，即可得出答案.
12.【答案】 （1）∠EAB；∠DAC
（2）解：过C作CF∥AB，
∵AB∥DE，∴CF∥DE∥AB，
∴∠D=∠FCD，∠B=∠BCF，
∵∠BCF+∠BCD+∠DCF=360°，
∴∠B+∠BCD+∠D=360°，

（3）解：如图3，过点E作EF∥AB，

∵AB∥CD，∴AB∥CD∥EF，
∴∠ABE=∠BEF，∠CDE=∠DEF，
∵BE平分∠ABC，DE平分∠ADC，∠ABC=60°，∠ADC=70°，
∴∠ABE= ∠ABC=30°，∠CDE= ∠ADC=35°
∴∠BED=∠BEF+∠DEF=30°+35°=65°．
【考点】平行线的判定与性质，角平分线的定义
【解析】【解答】解：（1）根据平行线性质可得：因为 ，所以 ∠EAB， ∠DAC；

【分析】（1）根据平行线性质“两直线平行，内错角相等”可得∠B+∠BCD+∠D∠BCF+∠BCD+∠DCF；（2）过C作CF∥AB，根据平行线性质可得；（3）如图3，过点E作EF∥AB，根据平行线性质和角平分线定义可得∠ABE= ∠ABC=30°，∠CDE= ∠ADC=35°，故∠BED=∠BEF+∠DEF.
13.【答案】 （1）解：∵CE平分∠ACD，AE平分∠BAC，
∴∠BAC=2∠EAC，∠ACD=2∠ACE，
∵∠EAC+∠ACE=90°，
∴∠BAC+∠ACD=180°，
∴AB∥CD

（2）解：∠BAE+ ∠MCD=90°；
过E作EF∥AB，

∵AB∥CD，
∴EF∥AB∥CD，
∴∠BAE=∠AEF，∠FEC=∠DCE，
∵∠E=90°，
∴∠BAE+∠ECD=90°，
∵∠MCE=∠ECD，
∴∠BAE+ ∠MCD=90°

（3）解：∵AB∥CD，
∴∠BAC+∠ACD=180°，
∵∠QPC+∠PQC+∠PCQ=180°，
∴∠BAC=∠PQC+∠QPC
【考点】平行线的判定与性质，角平分线的定义
【解析】【分析】（1）先根据CE平分∠ACD，AE平分∠BAC得出∠BAC=2∠EAC，∠ACD=2∠ACE，再由∠EAC+∠ACE=90°可知∠BAC+∠ACD=180，故可得出结论（2）过E作EF∥AB，根据平行线的性质可知EF∥AB∥CD，∠BAE=∠AEF，∠FEC=∠DCE，故∠BAE+∠ECD=90°，再由∠MCE=∠ECD即可得出结论；（3）根据AB∥CD可知∠BAC+∠ACD=180°，∠QPC+∠PQC+∠PCQ=180°，故∠BAC=∠PQC+∠QPC．
14.【答案】 （1）∠1+∠2=∠3
理由：过点P作l1的平行线PQ
∵l1∥l2 ，
∴l1∥l2∥PQ
∴∠1=∠4，∠2=∠5
∵∠4+∠5=∠3，
∴∠1+∠2=∠3

（2）∠1+∠2=∠3不变
（3）∠1-∠2=∠3或∠2-∠1=∠3
理由：①当点P在下侧时，如图，过点P作l1的平行线PQ

∵l1∥l2 ，
∴l1∥l2∥PQ
∴∠2=∠4，∠1=∠3+∠4
∴∠1-∠2=∠3
②当点P在上侧时，同理可得∠2-∠1=∠3．
【考点】平行线的性质
【解析】【分析】（1）过点P作l1的平行线，根据平行线的性质进行解题；
（2）（3）都是同样的道理．

15.【答案】 （1）解：①∵∠DFE=90°，
∴∠DEF+∠EDF=90°，
∵∠EDF=30°，
∴∠DEF=60°，
∵∠DEF=∠EAF+∠AFE，
∴∠AFE=∠DEF﹣∠EAF=60°﹣45°=15°；
②如图，当∠AFD=90°时，

∵∠ACB=90°，
∴∠BAC+∠ABC=90°，
∵∠BAC=45°
∴∠ABC=45°，
∵MN∥GH，
∴∠BAN=∠ABC=45°，
∵∠AFD=90°，
∴∠FAD+∠ADF=90°，
∵∠ADF=30°，
∴∠FAD=60°，
∴∠FAN=∠FAD﹣∠BAN=60°﹣45°=15°；
如图，当∠FAD=90°时，

∠FAN=∠FAD﹣∠BAN=90°﹣45°=45°，
∴∠FAN度数为15°或45°；

（2）
【考点】余角、补角及其性质，平行线的性质，旋转的性质，一元一次方程的实际应用-几何问题
【解析】【解答】解:（2）如图，∵∠BAC=45°，∠ACB=90°，
∴∠AKD+∠CDK=360°-90°-45°=225°，
∵MN∥GH，
∴∠MAK=∠AKD=n°，
∵∠AKD+∠CDK=225°，
∴(n+4m-2n-10) °=225°，
整理得：n°=(4m-235) °，

∵AC=1，且EF和GH之间的距离为1，
∴BC=1，
如图，点C在直线MN上时，点B、K、D重合，∠MAK= n°=180°-45°=135°，

如图，点C在直线GH上时，点B、K、D重合，∠MAK= n°=90°-45°=45°，

∵点C在MN和GH之间（不含MN、GH上），
∴45°＜n°＜135°，
即45°＜(4m-235) °＜135°，
∴m的取值范围是：70°＜m＜92.5°.
故答案为：70°＜m＜92.5°.
【分析】（1）①根据直角三角形的性质求出∠DEF=60°，结合图形计算即可；②分∠AFD=90°、∠FAD=90°两种情况计算，得到答案；
（2）先根据四边形的内角和得∠AKD+∠CDK=360°-90°-45°=225°，利用平行线的性质得：n°=(4m-235) °，确认点C边界上两点时，确定n的取值，代入n°=(4m-235) °，可得结论.
16.【答案】 （1）解：过P作PQ∥l1∥l2 ，

由两直线平行，内错角相等，可得：∠1＝∠QPE、∠2＝∠QPF；
∵∠3＝∠QPE＋∠QPF，
∴∠3＝∠1＋∠2．

（2）解：可以反推直线l1//l2.理由具体如下：
过点P作PQ1平行l1 ， 如下图（2）所示：

因为PQ1平行l1 ， 所以∠1＝∠Q1PE；又因为∠3＝∠Q1PE＋∠Q1PF，且∠3＝∠1＋∠2，所以可得∠2＝∠QPF，则根据平行线的判定法则：内错角相等，两直线平行可知PQ1平行l2；又由于PQ1平行l1 ， PQ1平行l2 ， 所以l1//l2.故反推成立.

（3）解：当点P在A点上方时，过点P作PQ2∥l1∥l2 ， 如下图所示：

则：∠1＝∠Q2PE、∠2＝∠Q2PF；
∵∠3＝∠Q2PF−∠Q2PE，
∴∠3＝∠2−∠1．
当点P在B点下方时，过点P作PQ3∥l1∥l2 ， 如下图所示：

根据题意我们设∠1＝∠PEA、∠2＝∠PFB、∠3＝∠EPF；则有图可知：∠1＝∠Q3PE、∠2＝∠Q3PF；
∵∠3＝∠Q3PE −∠Q3PF，
∴∠3＝∠1−∠2．
【考点】角的运算，平行线的判定与性质
【解析】【分析】（1）过P作直线l1、l2的平行线，利用平行线的性质得到∠1＝∠QPE、∠2＝∠QPF，然后结合这些等角和∠3的位置关系，即可∠1、∠2、∠3的数量关系；
（2）过点P作PQ1平行l1 ， 由PQ1平行l1 ， 得到∠1＝∠Q1PE；又由∠3＝∠Q1PE＋∠Q1PF，且∠3＝∠1＋∠2，得到∠2＝∠QPF，再根据平行线的判定法则进行求解即可得到答案.
（3）本题分两种情况讨论：当点P在A点上方时，过点P作PQ2∥l1∥l2 ， 结合题意可得∠1＝∠Q2PE、∠2＝∠Q2PF；又由∠3＝∠Q2PF−∠Q2PE，可得∠3＝∠2−∠1．当点P在B点下方时，过点P作PQ3∥l1∥l2 ， 则有图可知：∠1＝∠Q3PE、∠2＝∠Q3PF；根据∠3＝∠Q3PE −∠Q3PF，可得∠3＝∠1−∠2．
17.【答案】 （1）（0，6）；（8，0）
（2）由（1）知，A（0，6），C（8，0），
∴OA=6，OB=8，
由运动知，OQ=t，PC=2t，
∴OP=8-2t，
∵D（4，3），
∴ ，
，
∵△ODP与△ODQ的面积相等，
∴2t=12-3t，
∴t=2.4，
∴存在t=2.4时，使得△ODP与△ODQ的面积相等；

（3）2∠GOA+∠ACE=∠OHC，理由如下：
∵x轴⊥y轴，
∴∠AOC=∠DOC+∠AOD=90°，
∴∠OAC+∠ACO=90°.
又∵∠DOC=∠DCO，
∴∠OAC=∠AOD.
∵x轴平分∠GOD，
∴∠GOA=∠AOD.
∴∠GOA=∠OAC.
∴OG∥AC，
如图，过点H作HF∥OG交x轴于F，
∴HF∥AC，
∴∠FHC=∠ACE.
∵OG∥FH，
∴∠GOD=∠FHO，
∴∠GOD+∠ACE=∠FHO+∠FHC，
即∠GOD+∠ACE=∠OHC，
∴2∠GOA+∠ACE=∠OHC．

【考点】平行线的判定与性质，三角形的面积，非负数的性质：算术平方根，绝对值的非负性，利用合并同类项、移项解一元一次方程
【解析】【解答】（1）∵ ，
∴a-b+2=0，b-8=0，
∴a=6，b=8，
∴A（0，6），C（8，0）；
故答案为：（0，6），（8，0）；
【分析】（1）根据算术平方根的非负性，绝对值的非负性即可求解；
（2）根据运动速度得到OQ=t，OP=8-2t，根据△ODP与△ODQ的面积相等列方程求解即可；
（3）由∠AOC=90°，y轴平分∠GOD证得OG∥AC，过点H作HF∥OG交x轴于F，得到∠FHC=∠ACE，∠FHO=∠GOD，从而∠GOD+∠ACE=∠FHO+∠FHC，即可证得2∠GOA+∠ACE=∠OHC.
18.【答案】 （1）∵CM平分∠ACD，AM平分∠BAC，
∴∠BAC=2∠MAC，∠ACD=2∠ACM，
∵∠MAC+∠ACM=90°，
∴∠BAC+∠ACD=180°，
∴AB∥CD；

（2）∠BAM+∠MCD=90°，
理由：如图，过M作MF∥AB，
∵AB∥CD，
∴MF∥AB∥CD，
∴∠BAM=∠AMF，∠FMC=∠DCM，
∵∠M=90°，
∴∠BAM+∠MCD=90°；


（3）∠BAC=∠CHG+∠CGH．
理由：过点G作GP∥AB，
∵AB∥CD
∴GP∥CD，
∴∠BAC=∠PGC，∠CHG=∠PGH，
∴∠PGC=∠CHG+∠CGH，
∴∠BAC=∠CHG+∠CGH．

【考点】平行线的性质，角平分线的定义
【解析】【分析】（1）已知CM平分∠ACD，AM平分∠BAC，根据角平分线的定义可得∠BAC=2∠MAC，∠ACD=2∠ACM，再由∠MAC+∠ACM=90°，即可得∠BAC+∠ACD=180°，根据同旁内角互补，两直线平行即可得AB∥CD；（2）∠BAM+∠MCD=90°，过M作MF∥AB，即可得MF∥AB∥CD，根据平行线的性质可得∠BAM=∠AMF，∠FMC=∠DCM，再由∠M=90°，即可得∠BAM+∠MCD=90°；（3）∠BAC=∠CHG+∠CGH，过点G作GP∥AB，即可得GP∥CD，根据平行线的性质可得∠BAC=∠PGC，∠CHG=∠PGH，所以PGC=∠CHG+∠CGH，即可得∠BAC=∠CHG+∠CGH．
19.【答案】 （1）∠3=∠1+∠2 理由：
延长DP交直线l2与E，如图

∵直线l1∥l2
∴∠1=∠DCE
∵∠3=∠DEC+∠2
∴∠3=∠1+∠2

（2）不发生变化，∠3=∠1+∠2
理由：
∵直线l1∥l2
∴∠1=∠DCE
∴∠3=∠DEC+∠2=∠1+∠2

（3）①当点P在射线AB上运动时，如图2
∵直线l1∥l2
∴∠1=∠PFB
∵∠PFB=∠2+∠3
∴∠1=∠2+∠3
②如图3，当点P在射线BA上运动时，
∵直线l1∥l2
∴∠PGA=∠2
∵∠PGA=∠1+∠3
∴∠2=∠1+∠3
 
【考点】平行线的性质，三角形的外角性质
【解析】【分析】（1）（2）延长DP交直线l2于点E，根据平行线的性质和三角形外角的性质求解；
（3）（4）分别根据平行线的性质和三角形外角的性质求解.
 
20.【答案】 （1）解：∠CPD= ，理由如下：
如图3，过点P作PE∥AD交CD于点E，

∵AD∥BC，PE∥AD，
∴AD∥PE∥BC，
∴ =∠DPE， =∠CPE，
∴∠CPD=∠DPE+∠CPE=

（2）①当点P在A、M两点之间时，∠CPD=∠β−∠α；②当点P在B、O两点之间时，∠CPD=∠α−∠β
【考点】平行线的判定与性质
【解析】【解答】（2）①当点P在A、M两点之间时，∠CPD= ，理由如下：
如图4，过点P作PE∥AD交CD于点E，

∵AD∥BC，PE∥AD，
∴AD∥PE∥BC，
∴ =∠EPD， =∠CPE，
∴∠CPD=∠CPE−∠EPD= ；
②当点P在B、O两点之间时，∠CPD= ，理由如下：
如图5，过点P作PE∥AD交CD于点E，

∵AD∥BC，PE∥AD，
∴AD∥PE∥BC，
∴ =∠DPE， =∠CPE，
∴∠CPD=∠DPE−∠CPE= ，
综上所述，当点P在A、M两点之间时，∠CPD=∠β−∠α；当点P在B、O两点之间时，∠CPD=∠α−∠β.
【分析】（1）过点P作PE∥AD交CD于点E，根据题意得出AD∥PE∥BC，从而利用平行线性质可知 =∠DPE， =∠CPE，据此进一步证明即可；（2）根据题意分当点P在A、M两点之间时以及当点P在B、O两点之间时两种情况逐一分析讨论即可.
21.【答案】 （1），理由如下：
 CE 平分 ，AE 平分 ，


；

（2），理由如下：
如图，延长AE交CD于点F，则


由三角形的外角性质得：
；


（3），理由如下：

，即
由三角形的外角性质得：
又 ，即

即 ．
【考点】平行线的性质，三角形的外角性质，角平分线的定义
【解析】【分析】（1）根据角平分线的定义、平行线的判定即可得；（2）根据平行线的性质（两直线平行，内错角相等）、三角形的外角性质即可得；（3）根据平行线的性质（两直线平行，同旁内角互补）、三角形的外角性质、邻补角的定义即可得．
22.【答案】 （1）解 : ∵线段AB的两个端点坐标分别为A（0，2），B（−1，0），将线段AB向右平移3个单位长度，得到线段CD，
∴C（2，0），D（3，2）；

（2）解 : ∠ABP＋∠BPC−∠ECP＝180°，理由如下：
过点P作PF∥AB，如图所示：

由平移的性质得：DE∥AB，
∴AB∥PF∥DE，
∴∠ABP＋∠BPF＝180°，∠CPF＝∠ECP，
∵∠BPC＝∠BPF＋∠CPF，
∴∠BPC＝（180°−∠ABP）＋∠ECP，
即：∠ABP＋∠BPC−∠ECP＝180°；

（3）解 : 设点Q（x，0），连接BD，DQ，

则：BQ=|x-(-1)|=|x+1|，
∴S△BDQ= |x+1|×2=|x+1|，
∵S四边形ABCD=3×2=6，
∴|x+1|=6，
∴x+1=6或x+1=-6，
∴x=5或-7，
∴存在这样的Q点，Q（5，0）或（-7，0）
【考点】解含绝对值符号的一元一次方程，平行线的性质，三角形的面积，平移的性质，坐标与图形变化﹣平移
【解析】【分析】（1）由平移的性质即可得出结果；（2）过点P作PF∥AB，由平移的性质得出AB∥PF∥DE，由平行线的性质得出∠ABP＋∠BPF＝180°，∠CPF＝∠ECP，即可得出结论；（3）由题意得出四边形ABCD是平行四边形，得出AD＝BC＝3，AB＝CD，BC边上的高为2，得出S四边形ABCD＝2×3＝6，当点Q在x轴上时，S△QBD＝ ×2×BQ＝BQ，得出BQ＝6，即可得出结果.
23.【答案】 （1）平行于同一条直线的两条直线平行；两直线平行同旁内角互补 问题迁移：
（2）∠CPD=∠α+∠β，
理由是：如图3，过P作PE∥AD交CD于E，

∵AD∥BC，
∴AD∥PE∥BC，
∴∠α=∠DPE，∠β=∠CPE，
∴∠CPD=∠DPE+∠CPE=∠α+∠β；
问题解决：

（3）∠CPD=∠β-∠α或∠CPD=∠α-∠β.
【考点】平行线的判定与性质
【解析】【解答】解：（1）过点P作PE∥AB，
∵PE∥AB(作图知)
又∵AB∥CD，
∴PE∥CD．（平行于同一条直线的两条直线平行）
∴∠A+∠APE=180°．
∠C+∠CPE=180°．（两直线平行同旁内角互补）
∵∠PAB=130°，∠PCD=120°，
∴∠APE=50°，∠CPE=60°
∴∠APC=∠APE+∠CPE=110°．
故答案为：平行于同一条直线的两条直线平行两直线平行同旁内角互补
（ 3 ）当P在BA延长线时，

过P作PE∥AD交直线CD于E，
同（2）可知：∠α=∠DPE，∠β=∠CPE，
∴∠CPD=∠β-∠α；
当P在AB延长线时，

同（2）可知：∠α=∠DPE，∠β=∠CPE，
∴∠CPD=∠α-∠β．
【分析】（1）根据平行线的判定与性质填写即可；（2）过P作PE∥AD交CD于E，推出AD∥PE∥BC，根据平行线的性质得出∠α=∠DPE，∠β=∠CPE，即可得出答案；（3）画出图形（分两种情况①点P在BA的延长线上，②点P在AB的延长线上），根据平行线的性质得出∠α=∠DPE，∠β=∠CPE，即可得出答案．