2.4 一元一次不等式（组）及其应用-中考数学一轮复习 知识点+练习

这是一份2.4 一元一次不等式（组）及其应用-中考数学一轮复习 知识点+练习，文件包含24一元一次不等式组及其应用-解析版docx、24一元一次不等式组及其应用-原卷版docx等2份试卷配套教学资源，其中试卷共48页， 欢迎下载使用。
一、课标解读
1.结合具体问题，了解不等式的意义，探索不等式的基本性质。
2.能解数字系数的一元一次不等式，并能在数轴上表示出解集；会用数轴确定由两个一元一次不等式组成的不等式组的解集。
3.能根据具体问题中的数量关系，列出一元一次不等式，解决简单的问题。
二、知识点回顾
知识点1. 不等式的性质
①性质1：不等式的两边同时加上(或减去)同一个数(或式子)，不等号的方向 不变 。
用字母表示为： 如果，那么； 如果，那么 ；
②性质2：不等式的两边同时乘以(或除以)同一个 正数 ，不等号的方向 不变 。
用字母表示为： 如果，那么(或)；如果，那么(或)；
③性质3：不等式的两边同时乘以(或除以)同一个 负数 ，不等号的方向 改变 。
用字母表示为： 如果，那么(或)；如果，那么(或)；
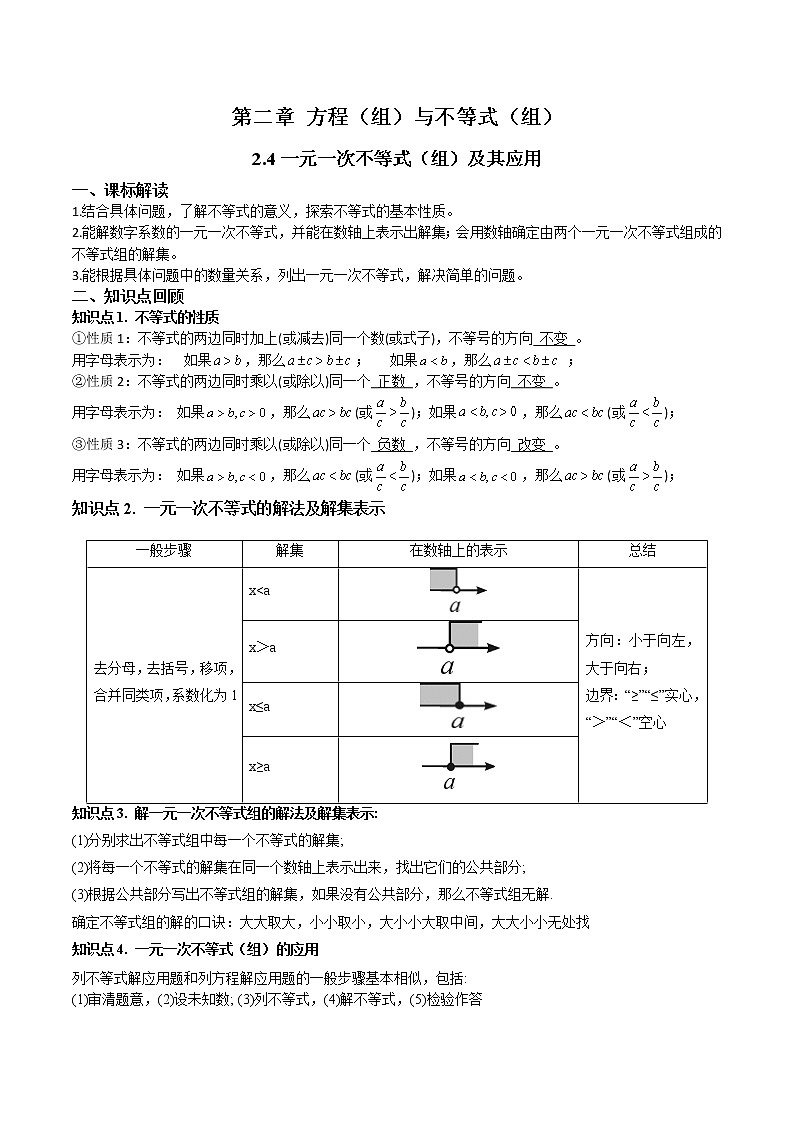
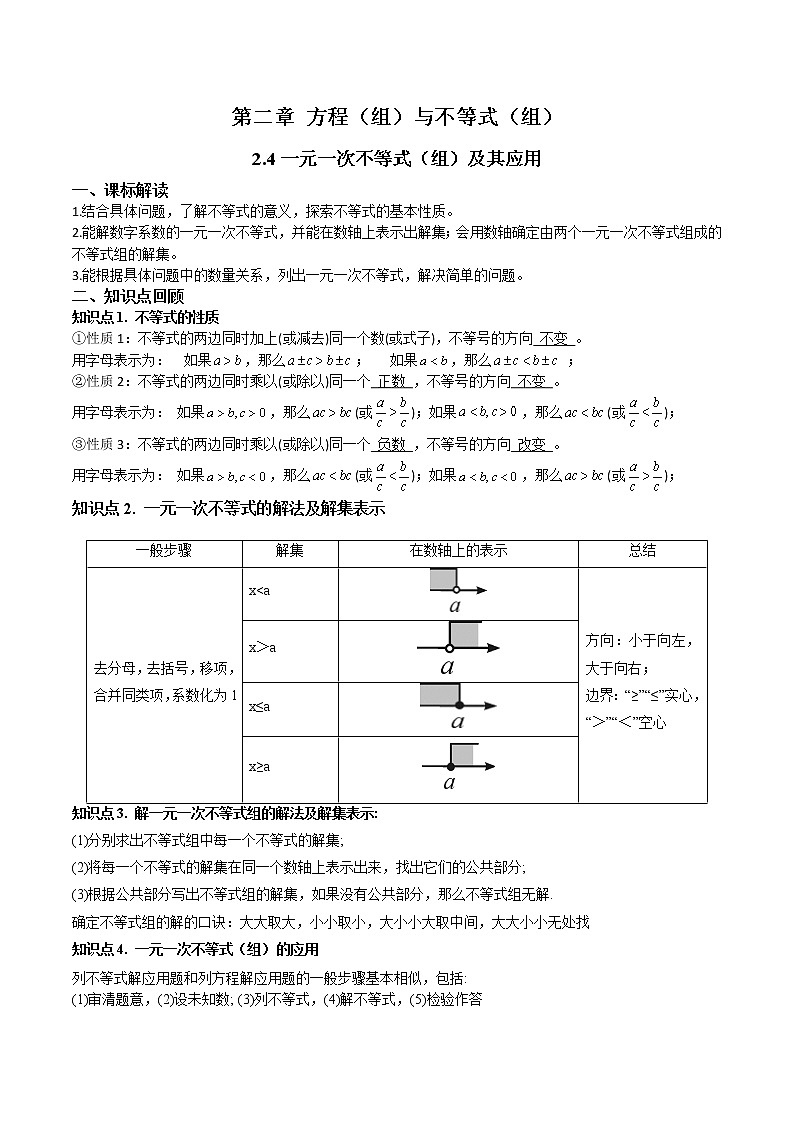
知识点2. 一元一次不等式的解法及解集表示
知识点3. 解一元一次不等式组的解法及解集表示:
(1)分别求出不等式组中每一个不等式的解集;
(2)将每一个不等式的解集在同一个数轴上表示出来，找出它们的公共部分;
(3)根据公共部分写出不等式组的解集，如果没有公共部分，那么不等式组无解.
确定不等式组的解的口诀：大大取大，小小取小，大小小大取中间，大大小小无处找
知识点4. 一元一次不等式（组）的应用
列不等式解应用题和列方程解应用题的一般步骤基本相似，包括:
(1)审清题意，(2)设未知数; (3)列不等式，(4)解不等式，(5)检验作答
三、热点训练
热点1：不等式的性质
一练基础
1．（2021·江苏·靖江市靖城中学一模）若，则下列各式中一定成立的是（ ）．
A．B．C．D．
2．（2021·浙江·杭州市采荷中学二模）若，则（ ）
A．B．C．D．
3．（2021·广东·珠海市九洲中学三模）若，则（ ）
A．B．C．D．
4．（2021·浙江·翠苑中学二模）下列说法正确的是（ ）
A．若，则B．若，则
C．若，则D．若，则
5．（2021·浙江拱墅·二模）已知a＜b，则（ ）
A．a+1＜b+2B．a﹣1＞b﹣2C．ac＜bcD．
二练巩固
6．（2021·浙江杭州·三模）已知a＞b，下列变形一定正确的是（ ）
A．3a＜3bB．4+a＞4﹣bC．ac3＞bc3D．3+2b＞3+2b
7．（2021·山东聊城·中考真题）若﹣3＜a≤3，则关于x的方程x＋a＝2解的取值范围为（ ）
A．﹣1≤x＜5B．﹣1＜x≤1C．﹣1≤x＜1D．﹣1＜x≤5
8．（2021·浙江滨江·三模）设，是实数，则（ ）
A．若，则B．若，则
C．若，则D．若，则
9．（2021·江苏常州·一模）如图，数轴上点、对应的数分别为、，则下列不等式正确的是（ ）
A．B．C．D．
10．（2021·浙江·杭州育才中学模拟预测）下列说法错误的是（ ）
A．若，则B．若，则
C．若，则D．若，则
三练拔高
11．（2021·山东淄川·二模）用三个不等式a＞b，ab＞0，＜中的两个不等式作为题设，能组成真命题的个数为（ ）
A．0B．1C．2D．3
12．（2021·四川·岳池县教研室二模）已知在第四象限，则在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
13．（2020·浙江·模拟预测）能说明命题“若a＞b，则3a＞2b“为假命题的反例为（ ）
A．a＝3，b＝2B．a＝﹣2，b＝﹣3C．a＝2，b＝3D．a＝﹣3，b＝﹣2
14．（2021·浙江·九年级专题练习）如图，平面直角坐标系中有P、Q两点，其坐标分别为P（4，a）、Q（b，6）．根据图中P、Q两点的位置，判断点（9﹣2b，a﹣6）落在第（ ）象限．
A．一B．二C．三D．四
15．（2021·北京房山·二模）已知，且实数满足，请你写出一个符合题意的实数的值___．
热点2：一元一次不等式（组）及其解法
一练基础
1．（2021·甘肃兰州·中考真题）关于的一元一次不等式的解集在数轴上表示为（ ）
A．B．
C．D．
2．（2021·浙江嘉兴·中考真题）已知点在直线上，且（ ）
A．B．C．D．
3．（2019·山东淄博·中考模拟）不等式组的解集在数轴上表示正确的是（ ）
A．B．
C．D．
4．（2021·辽宁锦州·二模）先化简，再求值：，其中是不等式的正整数解．
5．（2021·浙江·杭州育才中学模拟预测）点点同学解不等式的过程如下：
点点的解答过程显然有错误，请帮点点写出正确的解答过程．
6．（2021·江苏姑苏·二模）解不等式组：．
二练巩固
7．（2021·山东诸城·二模）在实数范围内规定新运算“”，规则是：，若不等式的解集在数轴上如图表示，则的值是______．
8．（2021·湖北蔡甸·二模）解不等式组请按下列步骤完成解答：
（1）解不等式①，得______；
（2）解不等式②，得______；
（3）把不等式①和②的解集在数轴上表示出来；
（4）原不等式组的解集为______．
9．（2021·山西·三模）（1）计算：；
（2）下面是小亮同学解一元一次不等式的过程，请认真阅读并完成相应的任务．
①以上求解过程中，去分母的依据是________；
②第________步开始出现错误，这一步错误的原因是________．
③请直接写出该不等式的解集．
④除纠正上述错误外，请你根据平时的学习经验，就解一元一次不等式需要注意的事项给其他同学提一条建议．
10．已知实数a是不等于3的常数，解不等式组并依据a的取值情况写出其解集．
11．（2021·北京市三帆中学模拟预测）某校举办数学素养大赛，比赛共设四个项目：七巧拼图、趣题巧解、数学应用和魔方复原，每个项目得分都按一定百分比折算后记入总分，并规定总分在85分以上（含85分）设为一等奖．下表为甲、乙、丙三位同学的得分情况（单位：3分）其中甲的部分信息不小心被涂黑了．
据悉，甲、乙、丙三位同学的七巧拼图和魔方复原两项得分折算后的分数之和均为20分．如果甲获得了大赛一等奖，那么甲的“数学应用”项目至少获得______分．
三练拔高
12．（2021·四川·绵竹市孝德中学一模）已知实数，满足，并且，，现有，则的取值范围为（ ）
A．B．C．D．
13．（2021·四川省宜宾市第二中学校三模）若关于x的不等式3x+m≥0有且仅有两个负整数解，则m的取值范围是（ ）
A．6≤m≤9B．6＜m＜9C．6＜m≤9D．6≤m＜9
14．（2021·黑龙江佳木斯·二模）若关于x的分式方程的解为非负数，则m的取值范围为（ ）
A．且B．且
C．D．且
15．（2021·四川眉山·中考真题）若关于的不等式只有3个正整数解，则的取值范围是______．
16．（2021·辽宁盘锦·中考真题）从不等式组的所有整数解中任取一个数，它是偶数的概率是________
17．（2018·河南泌阳·中考模拟）先化简，再求值：（1﹣）÷，其中x是不等式组的整数解
热点3：一元一次不等式（组）的实际应用
一练基础
1．（2021·贵州遵义·中考真题）小明用30元购买铅笔和签字笔，已知铅笔和签字笔的单价分别是2元和5元，他买了2支铅笔后，最多还能买几支签字笔？设小明还能买x支签字笔，则下列不等关系正确的是（ ）
A．5×2+2x≥30B．5×2+2x≤30C．2×2+2x≥30D．2×2+5x≤30
2．（2021·全国·九年级专题练习）为了治理环境，九年级部分同学去植树，若每人平均植树7棵，还剩9棵；若每人平均植树9棵．则有1名同学植树的棵树小于8棵．若设同学人数为x人，下列各项能准确的求出同学人数与种植的树木的数量的是（ ）
A．7x+9﹣9（x﹣1）＞0B．7x+9﹣9（x﹣1）＜8
C．D．
3．（2021·浙江·杭州市丰潭中学二模）根据数量关系：x的5倍加上1是负数，可列出不等式：_________．
4．（2021·福建·福州十八中二模）小明同学在计算一个多边形的内角和时，由于粗心少算了一个内角，结果得到的总和是800°，则少算了这个内角的度数为 ___ ．
5．已知两个语句：
①式子的值在1(含1)与3(含3)之间；
②式子的值不小于1且不大于3．
请回答以下问题：
（1）两个语句表达的意思是否一样(不用说明理由)？
（2）把两个语句分别用数学式子表示出来．
二练巩固
6．（2021·广东·佛山市华英学校一模）为积极响应政府提出的“绿色发展低碳出行”号召，某社区决定购置一批共享单车．经市场调查得知，购买3辆男式单车与4辆女式单车费用相同，购买5辆男式单车与4辆女式单车共需6400元．
（1）求男式单车和女式单车的单价；
（2）该社区要求男式单车比女式单车多4辆，购置两种单车的费用不超过2000元，该社区至多购置女式单车多少辆？
7．（2021·浙江上城·二模）身体质量指数（BMI）的计算公式是：BMI＝．这里W为身体的体重（单位：kg），h为身高（单位：m）．男性的BMI指数正常范围是18.5≤BMI≤23.9．
（1）有一位男运动员身高1.8m，体重81kg，请问他的BMI正常吗？
（2）有一位成年男性身高2m且他的BMI正常，请求出他的体重范围．
8．（2021·黑龙江·哈尔滨市第六十九中学校一模）在运动会前夕，光明中学购买篮球、足球作为奖品；若购买6个篮球和8个足球共花费1700元，且购买一个篮球比购买一个足球多花50元．
（1）求购买一个篮球，一个足球各需多少元：
（2）今年学校计划购买这种篮球和足球共10个，恰逢商场在搞促销活动，篮球打九折，足球打八五折，若此次购买两种球的总费用不超过1150元，则最多可购买多少个篮球？
9．（2021·广东实验中学三模）某药店在今年3月份，购进了一批口罩，这批口罩包括有一次性医用外科口罩和N95口罩，且两种口罩的只数相同.其中购进一次性医用外科口罩花费2000元N95口罩花费10000元．已知购进一次性医用外科口罩的单价比N95口罩的单价少8元．
（1）求该药店购进的一次性医用外科口罩和N95口罩的单价各是多少元?
（2）该药店计划再次购进两种口罩共1800只，预算购进的总费用不超过1万元，问至少购进一次外科口罩多少只?
三练拔高
10．（2021·重庆实验外国语学校三模）永川黄瓜山，林场万亩、环境优美，山势雄伟、地貌奇特，现已成为全国面积最大的南方早熟梨基地，品种以黄花梨为主，还有黄冠、圆黄、红梨、鄂梨2号等．永川梨香甜，脆嫩，皮薄，多汁．2020年，永川梨入选第一批全国名特优新农产品名录．
（1）某水果经销商第一批购进黄花梨5000千克，黄冠梨2000千克，黄冠梨每千克的进价比黄花梨的进价每千克多2元，经销商所花费的费用不超过60000元，求黄花梨每千克进价最多为多少元？
（2）在第（1）问最高进价的基础上，随着梨大量成熟，该水果经销商第二批购进的黄花梨的数量比第一批的数量增加了%，第二批购进的黄冠梨的数量不变，黄花梨的进价减少了%，黄冠梨的进价减少了%，第二批购进梨的总成本与第一批购进梨的总成本相同，求的值．
11．（2021·青海西宁·中考真题）城乡学校集团化办学已成为西宁教育的一张名片．“五四”期间，西宁市某集团校计划组织乡村学校初二年级200名师生到集团总校共同举办“十四岁集体生日”．现需租用A，B两种型号的客车共10辆，两种型号客车的载客量（不包括司机）和租金信息如下表：
若设租用A型客车x辆，租车总费用为y元．
（1）请写出y与x的函数关系式（不要求写自变量取值范围）；
（2）据资金预算，本次租车总费用不超过11800元，则A型客车至少需租几辆？
（3）在（2）的条件下，要保证全体师生都有座位，问有哪几种租车方案？请选出最省钱的租车方案．
12．（2021·江苏·苏州市胥江实验中学校二模）某校为改善办学条件，计划购进A，B两种规格的书架，经市场调查发现有线下和线上两种购买方式，具体情况如下表：
（1）如果在线下购买A，B两种书架共20个，花费6720元，求A，B两种书架各购买了多少个；
（2）如果在线上购买A，B两种书架共20个，且购买B种书架的数量不少于A种书架的2倍，总共花费不超过6400元，请问总共有几种购买方案．
13．（2021·湖南郴州·中考真题）“七一”建党节前夕，某校决定购买，两种奖品，用于表彰在“童心向党”活动中表现突出的学生．已知奖品比奖品每件多25元预算资金为1700元，其中800元购买奖品，其余资金购买奖品，且购买奖品的数量是奖品的3倍．
（1）求，奖品的单价；
（2）购买当日，正逢该店搞促销活动，所有商品均按原价八折销售，学校调整了购买方案：不超过预算资金且购买奖品的资金不少于720元，，两种奖品共100件．求购买，两种奖品的数量，有哪几种方案？
14．（2021·浙江·杭州市丰潭中学二模）如图是小明“探究拉力F与斜面高度h关系”的实验装置，A、B是水平面上两个固定的点，用弹簧测力计拉着重为6N的木块分别沿倾斜程度不同的斜面BC向上做匀速直线运动，经测算，在弹性范围内，沿斜面的拉力F（N）是高度h（m）的一次函数．实验结果如图1、图2所示：
（1）求出F与h之间的函数表达式；
（2）如图3，若该装置的高度h为0.22m，求测量得到拉力F；
（3）若弹簧测力计的最大量程是5N，求装置高度h的取值范围．
15．（2021·黑龙江·中考真题）“中国人的饭碗必须牢牢掌握在咱们自己手中”．为扩大粮食生产规模，某粮食生产基地计划投入一笔资金购进甲、乙两种农机具，已知购进2件甲种农机具和1件乙种农机具共需3.5万元，购进1件甲种农机具和3件乙种农机具共需3万元．
（1）求购进1件甲种农机具和1件乙种农机具各需多少万元？
（2）若该粮食生产基地计划购进甲、乙两种农机具共10件，且投入资金不少于9.8万元又不超过12万元，设购进甲种农机具m件，则有哪几种购买方案？哪种购买方案需要的资金最少，最少资金是多少？
（3）在（2）的方案下，由于国家对农业生产扶持力度加大，每件甲种农机具降价0.7万元，每件乙种农机具降价0.2万元，该粮食生产基地计划将节省的资金全部用于再次购买甲、乙两种农机具（可以只购买一种），请直接写出再次购买农机具的方案有哪几种？
一般步骤
解集
在数轴上的表示
总结
去分母，去括号，移项，合并同类项，系数化为1
x