专题01 相交线与平行线-2021-2022学年七年级数学下册期末复习精选精练（人教版）

这是一份专题01 相交线与平行线-2021-2022学年七年级数学下册期末复习精选精练（人教版），文件包含专题01相交线与平行线解析版docx、专题01相交线与平行线原卷版docx等2份试卷配套教学资源，其中试卷共22页， 欢迎下载使用。
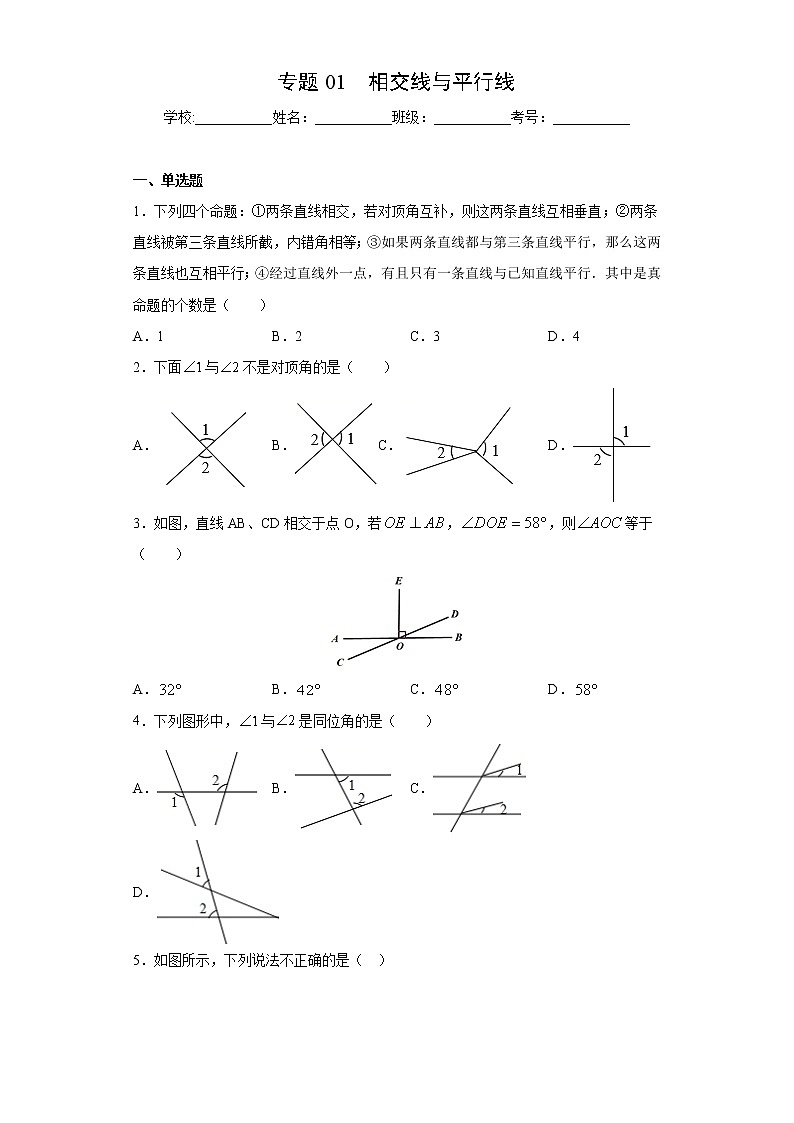
专题01  相交线与平行线学校:___________姓名：___________班级：___________考号：___________ 一、单选题1．下列四个命题：①两条直线相交，若对顶角互补，则这两条直线互相垂直；②两条直线被第三条直线所截，内错角相等；③如果两条直线都与第三条直线平行，那么这两条直线也互相平行；④经过直线外一点，有且只有一条直线与已知直线平行．其中是真命题的个数是（    ）A．1 B．2 C．3 D．4【答案】C【解析】解：两条直线相交，若对顶角互补，则这两条直线互相垂直，所以①正确；
两条互相平行的直线被第三条直线所截，内错角相等；，所以②错误；
如果两条直线都与第三条直线平行，那么这两条直线也互相平行，所以③正确；
经过直线外一点，有且只有一条直线与已知直线平行，所以④正确．
故选：C．2．下面与不是对顶角的是（　　）A． B．C． D．【答案】C【解析】A．是两直线相交得到的，有公共顶点，一个角的两边是另一个角的两边反向延长线，故选项A是对顶角，不符合题意；B．是两直线相交得到的，有公共顶点，一个角的两边是另一个角的两边反向延长线，故选项B是对顶角，不符合题意；C．不是两直线相交得到的，有公共顶点，一个角的两边不是另一个角的两边反向延长线，故选项C不是对顶角，符合题意；D．是两直线相交得到的，有公共顶点，一个角的两边是另一个角的两边反向延长线，故选项D是对顶角，不符合题意．故选C．3．如图，直线AB、CD相交于点O，若，，则等于（    ）A． B． C． D．【答案】A【解析】解：∵OE⊥AB，∴∠BOE＝90°，∵∠DOE＝58°，∴∠BOD＝90°-∠DOE＝32°，∴∠AOC＝∠BOD＝32°，故选：A．4．下列图形中，与是同位角的是（    ）A． B． C．D．【答案】D【解析】、、中的与不是同位角，中的与是同位角；故选：．5．如图所示，下列说法不正确的是（  ）A．和是同位角 B．和是内错角C．和是同旁内角 D．和是同旁内角【答案】C【解析】解：和是同位角，A正确；和是内错角，B正确；和不是同旁内角，C错误；和是同旁内角，D正确；故选：C．6．如图，下列条件：①；②；③；④，其中能判断直线与平行的个数是（ ）A．1 B．2 C．3 D．4【答案】C【解析】解：①∵∠1与∠2无特殊位置关系，∴由∠1=∠2不能得到l1//l2，故本条件不合题意；②∵∠4=∠5，∴l1//l2（同位角相等，两直线平行），故本条件符合题意；③∵∠2+∠4=180°，∴l1//l2（同旁内角互补，两直线平行），故本条件符合题意；④∵∠1=∠3，∴l1//l2（内错角相等，两直线平行），故本条件符合题意．故选：C．7．如图，，，平分，则的度数等于（    ）A．152° B．124° C．122° D．116°【答案】A【解析】解：∵AB∥CD，， ∴∠EFD=∠1=56°，∠FGB+∠GFD=180°，
∵FG平分∠EFD，∴∠GFD=28°，∴∠FGB=180°-∠GFD=152°，故选：A．8．如图，在下列给出的条件中，可以判定的有（      ）①；②；③；④；⑤．A．①②③ B．①②④ C．①④⑤ D．②③⑤【答案】D【解析】解：①∠1=∠2不能判定AB∥CD，不符合题意；
②∵∠1=∠3，∴AB∥CD，符合题意；③∵∠2=∠4，∴AB∥CD，符合题意；
④∠DAB+∠ABC=180°；不能判定AB∥CD，不符合题意；⑤∵∠BAD+∠ADC=180°，∴AB∥CD，符合题意．故选：D．二、填空题9．下列说法中：（1）不相交的两条直线叫做平行线；（2）经过一点，有且只有一条直线与已知直线平行；（3）垂直于同一条直线的两直线平行；（4）直线，，则；（5）两条直线被第三条直线所截，同位角相等．其中正确的是________．【答案】（4）【解析】（1）在同一平面内不相交的两条直线叫做平行线，故该项错误；（2）过直线外一点，有且只有一条直线与已知直线平行，故该项错误；（3）在同一平面内，垂直于同一条直线的两直线平行，故该项错误；（4）直线，，则，故该项正确；（5）两条平行线被第三条直线所截，同位角相等，故该项错误．故选：（4）．10．如图，图中内错角有________对，同旁内角有________对，同位角有________对．【答案】5    4    8    【解析】解：如图所示：

 根据题意得，图中内错角共5对，分别是∠FOM与∠OME，∠FOM与∠OMD，∠GOM与∠OMD，∠GOM与∠OME，∠HOM与∠CMO；
同旁内角共4对，分别是∠GOM与∠CMO，∠FOM与∠CMO，∠HOM与∠OME，∠HOM与∠OMD；
同位角共8对，分别是∠AOH与∠AME，∠AOH与∠AMD，∠HOB与∠BMD，∠HOB与∠BME，∠AOG与∠AMC，∠AOF与∠AMC，∠BMC与∠BOG，∠BMC与∠BOF．11．如图，要把池中的水引到处，且使所开渠道最短，可过点作于，然后沿所作的线段开渠，所开渠道即最短，试说明设计的依据是：____________________．【答案】直线外一点与直线上各点连接的所有线段中，垂线段最短．【解析】解：∵，∴CD是垂线段，CD最短，依据为：直线外一点与直线上各点连接的所有线段中，垂线段最短．故答案为：直线外一点与直线上各点连接的所有线段中，垂线段最短．12．如图，点是延长线上一点，在下列条件中：①；②；③且平分；④，能判定的有__．（填序号）【答案】③④【解析】①中，，（内错角相等，两直线平行），不合题意；②中，，（同位角相等，两直线平行），不合题意；③中，且平分，，，故此选项符合题意；④中，， （同旁内角互补，两直线平行），故此选项符合题意；答案：③④．13．已知：如图放置的长方形和等腰直角三角形EFG中，∠F=90°，FE=FG=4cm，AB=2cm，AD=4cm，且点F，G，D，C在同一直线上，点G和点D重合．现将△EFG沿射线FC向右平移，当点F和点C重合时停止移动．若△EFG 与长方形重叠部分的面积是4cm2，则△EFG 向右平移了____cm．【答案】3或2+ 【解析】详解：分三种情况讨论：①如图1．∵△EFG是等腰直角三角形，∴△HDG是等腰直角三角形，重合部分为△HDG，则重合面积=DG2=4，解得：DG=，而DC=2＜，故这种情况不成立； ②如图2．∵△EFG是等腰直角三角形，∴△HDG、△CGI是等腰直角三角形，重合部分为梯形HDCI，则重合面积=S△HDG－S△CGI =DG2－CG2=4，即：DG2－（DG-2）2=4，解得：DG=3；③如图3．∵△EFG是等腰直角三角形，∴△CGI是等腰直角三角形，重合部分为梯形EFCI，则重合面积=S△EFG－S△CGI =EF 2－CG2=4，即：×42－（DG-2）2=4，解得：DG= 或（舍去）．故答案为：3或．14．如图，在中，，射线，点E从点A出发沿射线以的速度运动，当点E先出发后，点F也从点B出发，沿射线以的速度运动，分别连接．设点E运动的时间为，其中，当_______时，．【答案】或【解析】解：∵AG∥BC，∴A到BC的距离等于C到AG的距离，∴当AE=CF时，S△ACE=S△AFC，分两种情况讨论：①点F在点C左侧时，AE=CF，则2（t+1）=6-3.5t，解得t=，②当点F在点C的右侧时，AE=CF，则2（t+1）=3.5t-6，解得t=，故答案为：或． 三、解答题15．完成下面的证明：如图，FG//CD，∠1=∠3，∠B=50°，求∠BDE的度数．解：∵FG//CD (已知)∴∠2=_________（                          ）又∵∠1=∠3∴∠3=∠_________（                   ）∴BC//__________（                           ）∴∠B+________=180°（                            ）又∵∠B=50°∴∠BDE=130°．【答案】∠1；两直线平行，同位角相等；∠2；等量代换；DE；内错角相等，两直线平行；∠BDE；两直线平行，同旁内角互补【解析】解：∵FG//CD (已知)∴∠2=∠1（两直线平行，同位角相等）又∵∠1=∠3，∴∠3=∠2（等量代换）∴BC//DE（内错角相等，两直线平行）∴∠B+∠BDE=180°（两直线平行，同旁内角互补）又∵∠B=50°∴∠BDE=130°．故答案为：∠1；两直线平行，同位角相等；∠2；等量代换；DE；内错角相等，两直线平行；∠BDE；两直线平行，同旁内角互补．16．如图，直线a，b，c被直线m，n所截，已知条件①∠BAC=∠BDC；②∠AFE=∠FED；③mn．（1）从①②③中选出其中的两个作为条件，第三个作为结论，可以构造出多少个命题?（2）写出一个真命题，并证明．【答案】（1）3个；（2）见解析【解析】（1）从①②③中选出其中的两个作为条件，第三个作为结论，可以构造出3个命题，分别为①②⇒③；②③⇒①；①③⇒②．（2）以上3个命题都是真命题．(i)∵∠AFE=∠FED，∴b∥c，∴∠CAB+∠ABD=180°，∵∠BAC=∠BDC，∴∠ABD+∠BDC=180°，∴m∥n；(ii)∵∠AFE=∠FED，∴b∥c，∴∠CAB+∠ABD=180°，∵m∥n，∴∠ABD+∠BDC=180°，∴∠BAC=∠BDC；(iii)∵m∥n，∴∠ABD+∠BDC=180°，∵∠BAC=∠BDC，∴∠CAB+∠ABD=180°，∴b∥c，∴∠AFE=∠FED．17．已知：如图，直线AB、CD相交于点O，EO⊥CD于O．（1）若∠AOC=36°，求∠BOE的度数；（2）若∠BOD：∠BOC=1：5，求∠AOE的度数；（3）在（2）的条件下，请你过点O画直线MN⊥AB，并在直线MN上取一点F（点F与O不重合），然后直接写出∠EOF的度数．【答案】（1）54°；（2）120°；（3）∠EOF的度数为30°或150°．【解析】解：（1）∵EO⊥CD，∴∠DOE=90°，又∵∠BOD=∠AOC=36°，∴∠BOE=90°-36°=54°；（2）∵∠BOD：∠BOC=1：5，∴∠BOD=∠COD=30°，∴∠AOC=30°，又∵EO⊥CD，∴∠COE=90°，∴∠AOE=90°+30°=120°；（3）分两种情况：若F在射线OM上，则∠EOF=∠BOD=30°；若F'在射线ON上，则∠EOF'=∠DOE+∠BON-∠BOD=150°；综上所述，∠EOF的度数为30°或150°．故答案为（1）54°；（2）120°；（3）∠EOF的度数为30°或150°．18．将一副三角板中的两个直角顶点叠放在一起（如图①），其中，，.（1）猜想与的数量关系，并说明理由；（2）若，求的度数；（3）若按住三角板不动，绕顶点转动三角，试探究等于多少度时，并简要说明理由. 【答案】（1），理由详见解析；（2）135°；（3）等于或时，.【解析】解：（1），理由如下：，；（2）如图①，设，则，由（1）可得，，，；（3）分两种情况：①如图1所示，当时，，又，；②如图2所示，当时，，又，.综上所述，等于或时，.19．如图，已知AB∥CD，CN是∠BCE的平分线． (1)若CM平分∠BCD，求∠MCN的度数； (2)若CM在∠BCD的内部，且CM⊥CN于C，求证：CM平分∠BCD； (3)在(2)的条件下，连结BM，BN，且BM⊥BN，∠MBN绕着B点旋转，∠BMC＋∠BNC是否发生变化？若不变，求其值；若变化，求其变化范围．【答案】（1）90°；（2）见解析；（3）∠BMC＋∠BNC＝180°不变，理由见解析【解析】(1)∵CN，CM分别平分∠BCE和∠BCD，∴BCN＝∠BCE，∠BCM＝∠BCD，∵∠BCE＋∠BCD＝180°，∴∠MCN＝∠BCN＋∠BCM＝∠BCE＋∠BCD＝(∠BCE＋∠BCD)＝90°；(2)∵CM⊥CN，∴∠MCN＝90°，即∠BCN＋∠BCM＝90°，∴2∠BCN＋2∠BCM＝180°，∵CN是∠BCE的平分线，∴∠BCE＝2∠BCN，∴∠BCE＋2∠BCM＝180°，又∵∠BCE＋∠BCD＝180°，∴∠BCD＝2∠BCM，又∵CM在∠BCD的内部，∴CM平分∠BCD；(3)如图，∠BMC＋∠BNC＝180°，延长AB至F，过N，M分别作NG∥AB，MH∥AB，则有NG∥AB∥MH∥CD，∴∠BNG＝∠ABN，∠CNG＝∠ECN，∠BMH＝∠FBM，∠CMH＝∠DCM，∵BM⊥BN，CM⊥CN，∴∠MBN＝∠MCN＝90°，∵∠ABN＋∠MBN＋FBM＝180°，∠ECN＋∠MCN＋∠DCM＝180°，∴∠ABN＋∠FBM＋∠ECN＋∠DCM＝180°，∴∠BMC＋∠BNC＝∠BMH＋∠CMH＋∠BNG＋∠CNG＝∠ABN＋∠FBM＋∠ECN＋∠DCM＝180°，∴∠BMC＋∠BNC＝180°不变.20．已知：直线∥，A为直线上的一个定点，过点A的直线交 于点B，点C在线段BA的延长线上．D，E为直线上的两个动点，点D在点E的左侧，连接AD，AE，满足∠AED＝∠DAE．点M在上，且在点B的左侧．（1）如图1，若∠BAD＝25°，∠AED＝50°，直接写出ABM的度数             ； （2）射线AF为∠CAD的角平分线． ① 如图2，当点D在点B右侧时，用等式表示∠EAF与∠ABD之间的数量关系，并证明； ② 当点D与点B不重合，且∠ABM＋∠EAF＝150°时，直接写出∠EAF的度数  ．【答案】（1）；（2）①，见解析；②或【解析】解：（1）设在上有一点N在点A的右侧，如图所示：∵∴，∴∴∴（2）①．证明：设，．∴．∵为的角平分线，∴．∵，    ∴．∴．∴．②当点在点右侧时，如图：由①得：又∵∴∵∴当点在点左侧，在右侧时，如图：∵为的角平分线∴∵∴，∵∴∴∵∴又∵∴∴当点和在点左侧时，设在上有一点在点的右侧如图：此时仍有，∴∴综合所述：或