专题02 平行线的性质与判定及平移-2021-2022学年七年级数学下学期期中专项复习（人教版）

专题02  平行线的性质与判定及平移

姓名：___________考号：___________分数：___________

（考试时间：100分钟  满分：120分）

一、 选择题（本大题共12小题，每小题3分，共36分。在每小题给出的四个选项中，只有一项是符合题目要求的）

1．如图，如果,下面结论正确的是（ ）

A． B．

C． D．

【答案】C

【分析】

根据同位角相等，两直线平行，可判定BC∥EF．

【详解】

解：∵∠B=∠AEF，且∠B和∠AEF互为同位角，

∴BC∥EF，

故选C．

【点睛】

本题考查了平行线的判定，解答本题的关键是掌握平行线的判定定理：同位角相等，两直线平行．

2．如图，下列条件，其中能判断直线的有（  ）

A． B． C． D．

【答案】D

【分析】

根据平行线的判定解题：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行；

【详解】

解：A. 不是直线被第三条直线所截形成的角，不能判断，故A错误；

B. 是邻补角，和为180°，不能判断，故B错误；

C. 是直线被第三条直线所截形成的同旁内角，不能判断，故C错误；

D. ，同位角相等，两直线平行，故能判定，故D正确 ，

故选：D．

【点睛】

本题考查平行线的判定，是重要考点，难度较易，掌握相关知识是解题关键．

3．如图，如果，那么（    ）

A．（两直线平行，内错角相等） B．（内错角相等，两直线平行）

C．（内错角相等，两直线平行） D．（两直线平行，内错角相等）

【答案】C

【分析】

根据平行线的判定方法直接得出结果．

【详解】

解：∵，

∴（内错角相等，两直线平行），

故选C．

【点睛】

本题考查平行线的判定方法．同位角相等两直线平行，内错角相等两直线平行，同旁内角互补两直线平行．

4．如图，在下列四组条件中，能判断的是（    ）

A． B． C． D．

【答案】B

【分析】

根据平行线的判定方法一一判断即可．

【详解】

解：∵∠1=∠2，∴AD∥BC，故A选项不符合题意；

∵∠ABD=∠BDC∴AB∥CD，故B选项符合题意；

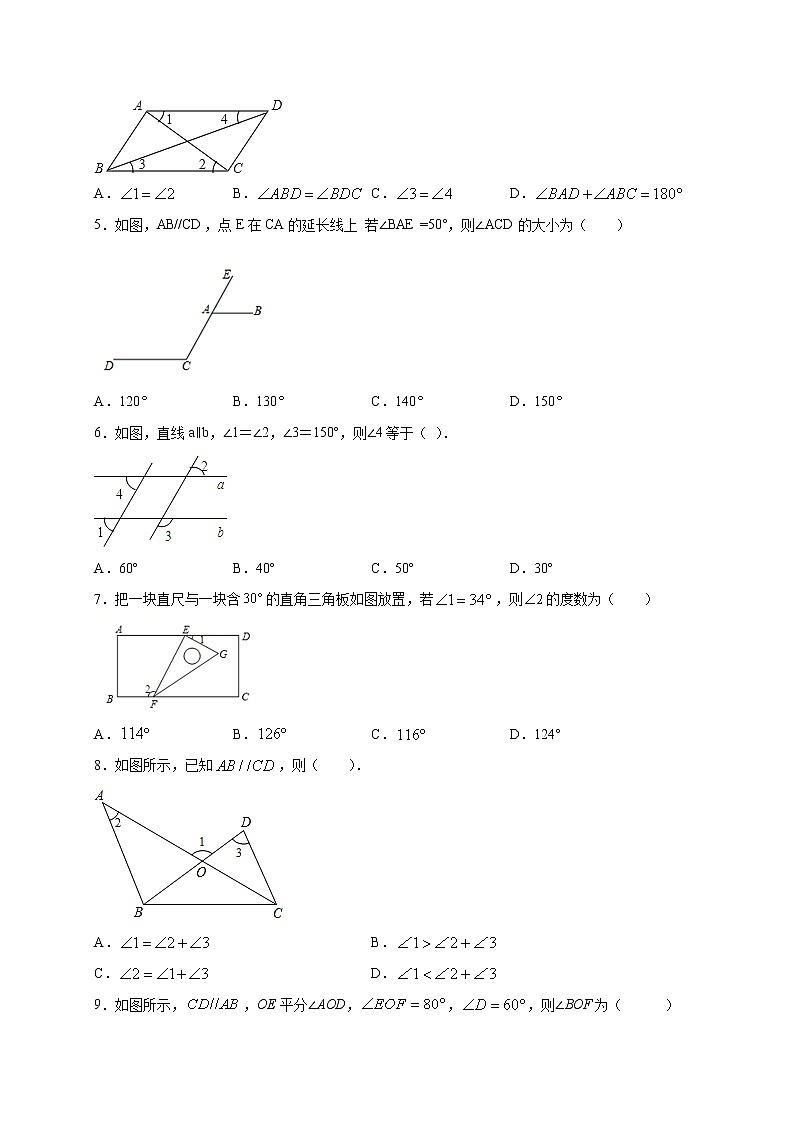
∵∠3=∠4，∴AD∥BC，故C选项不符合题意；

∵∠ABC+∠BAD=180°，∴AD∥CB．故D选项不符合题意；

故选：B．

【点睛】

本题考查平行线的判定，解题的关键是熟练掌握基本知识，属于中考常考题型．

5．如图，AB//CD，点E在CA的延长线上 若∠BAE =50°，则∠ACD的大小为（    ）

A．120 B．130 C．140 D．150

【答案】B

【分析】

先根据补角的定义求出∠BAC的度数，再由平行线的性质即可得出结论．

【详解】

解：∵∠BAE=50°，

∴∠CAB=180°-50°=130°．

∵AB∥CD，

∴∠BAC=∠ACD=130°．

故选：B．

【点睛】

本题考查的是平行线的性质，用到的知识点为：两直线平行，内错角相等．

6．如图，直线a∥b，∠1＝∠2，∠3＝150º，则∠4等于（ ）．

A．60º B．40º C．50º D．30º

【答案】D

【分析】

由直线a∥直线b，∠3=150°，根据两直线平行，同位角相等，即可得∠1=∠4，∠5=∠3=150°，又由邻补角的定义，即可求得∠2的度数，然后由∠1=∠2，即可求得∠4的大小．

【详解】

解：如图，

∵直线a∥b，∠3=150°，

∴∠1=∠4，∠5=∠3=150°，

∴∠2=180°-∠5=30°，

∵∠1=∠2，

∴∠4=∠2=30°．

故选：D．

【点睛】

此题考查了平行线的性质与邻补角的定义．此题比较简单，注意掌握两直线平行，同位角相等定理的应用，注意数形结合思想的应用．

7．把一块直尺与一块含的直角三角板如图放置，若，则的度数为（    ）

A． B． C． D．124°

【答案】D

【分析】

根据角的和差可先计算出∠AEF，再根据两直线平行同旁内角互补即可得出∠2的度数．

【详解】

解：由题意可知AD//BC，∠FEG=90°，

∵∠1=34°，∠FEG=90°，

∴∠AEF=90°-∠1=56°，

∵AD//BC，

∴∠2=180°-∠AEF=124°，

故选：D．

【点睛】

本题考查平行线的性质．熟练掌握两直线平行，同旁内角互补并能正确识图是解题关键．

8．如图所示，已知，则（    ）．

A． B．

C． D．

【答案】A

【分析】

根据平行线的性质，得；根据补角的性质，得；根据角的和差的性质计算，即可得到，从而完成求解．

【详解】

∵

∴

∵
 

又∵

∴

∴

故选：A．

【点睛】

本题考查了平行线、角的知识；解题的关键是熟练掌握平行线、补角、角的和差的性质，从而完成求解．

9．如图所示，，OE平分∠AOD，，，则∠BOF为（　　　）

A． B． C． D．

【答案】B

【分析】

由平行线的性质和角平分线的定义，求出，，然后即可求出∠BOF的度数．

【详解】

解：∵，

∴，，

∵OE平分∠AOD，

∴，

∴；

∴；

故选：B．

【点睛】

本题考查了平行线的性质，角平分线的定义，以及角的和差关系，解题的关键是熟练掌握所学的知识，正确的求出角的度数．

10．如图，已知直线、被直线所截，，E是直线右边任意一点（点E不在直线，上），设，．下列各式：①，②，③，④，的度数可能是（    ）

A．①②③ B．①②④ C．①③④ D．①②③④

【答案】A

【分析】

根据点E有3种可能位置，分情况进行讨论，依据平行线的性质以及三角形外角性质进行计算求解即可．

【详解】

解：（1）如图，由AB∥CD，可得∠AOC=∠DCE1=β，

∵∠AOC=∠BAE1+∠AE1C，

∴∠AE1C=β-α．

（2）如图，过E2作AB平行线，则由AB∥CD，可得∠1=∠BAE2=α，∠2=∠DCE2=β，

∴∠AE2C=α+β．

（3）当点E在CD的下方时，同理可得，∠AEC=α-β．

综上所述，∠AEC的度数可能为β-α，α+β，α-β．

即①α+β，②α-β，③β-α，都成立．

故选A．

【点睛】

本题主要考查了平行线的性质的运用，解题时注意：两直线平行，同位角相等；两直线平行，内错角相等．

11．如图，已知直线，平分交直线于点，若，则等于（    ）

A．25° B．29° C．30° D．45°

【答案】B

【分析】

根据平行线的性质可知∠ABC=58°，再根据角平分线的性质可求∠EBC=29°，再利用平行线的性质可求∠E．

【详解】

解：∵，

∴，

∵平分，

∴，

∵，

∴，

故选B．

【点睛】

本题考查了平行线的性质和角平分线的性质，灵活运用这两个性质是解题关键．

12．如图，，点在上，，，则下列结论正确的个数是（    ）

（1）；（2）；（3）；（4）

A．1个 B．2个 C．3个 D．4个

【答案】B

【分析】

过点E做直线EF平行于直线AB，然后根据同位角和同旁内角即可判断（2）和（3），其中（1）和（4）无法判断．

【详解】

过点E做直线EF平行于直线AB，如下图所示，

（1）无法判断；

（2）∵AB//CD，AB//EF

∴EF//CD

∴，

∴

故（2）正确；

（3）由（2）得，

∴

故（3）正确；

（4）无法判断；

故选B．

二、填空题（本大题共6小题，每小题3分，共18分）

13．如图，添加一个你认为合适的条件______使．

【答案】∠ADF=∠C或∠A=∠ABE或∠A+∠ABC=180°或∠C+∠ADC=180°（答案不唯一，写一个正确的即可）

【分析】

根据平行线的判定方法即可求解．

【详解】

第一种情况，同位角相等，两直线平行，即∠ADF=∠C时，；

第二种情况，内错角相等，两直线平行，即∠A=∠ABE时，；

第三种情况，同旁内角互补，两直线平行，即∠A+∠ABC=180°或∠C+∠ADC=180°时，；

故答案为∠ADF=∠C或∠A=∠ABE或∠A+∠ABC=180°或∠C+∠ADC=180°．

【点睛】

本题考查了平行线的判定方法，同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行．

14．一副三角板按如图所示叠放在一起，其中点B、D重合，若固定三角形AOB，改变三角板ACD的位置（其中A点位置始终不变），当∠BAD＝_____时，CD∥AB．

【答案】150°或30°．

【分析】

分两种情况，再利用平行线的性质，即可求出∠BAD的度数

【详解】

解：如图所示：当CD∥AB时，∠BAD＝∠D＝30°；

如图所示，当AB∥CD时，∠C＝∠BAC＝60°，

∴∠BAD＝60°+90°＝150°；

故答案为：150°或30°．

【点睛】

本题主要考查了平行线的判定，平行线的判掌握平行线的判定定理和全面思考并分类讨论是解答本题的关键.

15．如图，已知AB∥CD,∠EAF =∠EAB,∠ECF=∠ECD ,∠AFC=62°,则∠AEC度数是________

【答案】93°

【分析】

连接AC，设∠EAF=x°，∠ECF=y°，则∠EAB=3x°，∠ECD=3y°，可得∠BAF=2x°，∠DCF=2y°，由AB∥CD，三角形的内角和定理，可得∠AFC=2（x°+y°）=62°，计算得到x°+y°=31°，则∠AEC=3（x°+y°），即可得到答案.

【详解】

解，如图，连接AC，设∠EAF=x°，∠ECF=y°，

∴∠EAB=3x°，∠ECD=3y°，

∴∠BAF=2x°，∠DCF=2y°，

∵AB∥CD，

∴∠BAC+∠ACD=180°，

∴∠BAF+∠FAC+∠ACF+∠DCF=180°，

∵∠FAC+∠ACF+∠AFC=180°，

∴∠AFC=∠BAF+∠DCF=2（x°+y°）=62°，

∴x°+y°=31°.

同理可求：∠AEC=∠BCE+∠DCE=3（x°+y°），

∴∠AEC=.

故答案为：93°.

【点睛】

本题考查了平行线性质和三角形内角和定理的应用，根据题意作出辅助线，构造出三角形，利用三角形内角和定理求解是解答此题的关键．

16．已知，将一直角三角板放置如图，，那么的度数为________．

【答案】．

【分析】

利用平行线的性质，对顶角相等，把问题转化直角三角形两锐角互余求解即可．

【详解】

如图，

，

，

，

，

，

．

【点睛】

本题考查了平行线的性质，对顶角相等，直角三角形两个锐角互余，熟练平行线性质，直角三角形的性质是解题的关键．

17．如图，已知：，，平分，，则的度数是______．

【答案】40°

【分析】

先根据AB∥DE，∠B=70°，CM平分∠DCB可求出∠BCM及∠BCE的度数，再根据CM⊥CN可求出∠BCN的度数，再由∠NCE=∠BCE-∠BCN即可解答．

【详解】

解：∵AB∥DE，∠B=80°，

∴∠DCB=180°-∠B=180°-80°=100°，∠BCE=∠B=80°，

∵CM平分∠DCB，

∴∠BCM=∠DCB=×100°=50°，

∵CM⊥CN，垂足为C，

∴∠BCN=90°-∠BCM=90°-50°=40°，

∴∠NCE=∠BCE-∠BCN=80°-40°=40°．

故答案为：40°．

【点睛】

此题主要考查平行线的性质：两直线平行，内错角相等；两直线平行，同旁内角互补，属于基础题，注意细心掌握．

18．如图，点P、Q分别在一组平行直线、上，在两直线间取一点E使得，点F、G分别在、的角平分线上，且点F、G均在平行直线、之间，则__________．

【答案】35°

【分析】

过点F作，过点G作，利用平行线的性质和角平分线的定义即可求解.

【详解】

过点F作，过点G作，

∵平分，平分，

设，，

∵

∴，

∴，

∵，

∴，

∴，，，

∴

故．

三、解答题（本大题共6小题，共66分，解答应写出文字说明、演算步骤或推理过程）

19．如图①，在三角形ABC中，点E，F分别为线段AB，AC上任意两点，EG交BC于点G，交AC的延长线于点H，∠1＋∠AFE＝180°.

(1)证明：BC∥EF；

(2)如图②，若∠2＝∠3，∠BEG＝∠EDF，证明：DF平分∠AFE.

【答案】(1)见解析；(2) 见解析.

【分析】

（1）由条件可证明∠AFE=∠BCF，根据平行线的判定可证明BC∥EF；

（2）由条件可先证明DF∥EH，可得∠DFE=∠FEG，再结合（1）的结论和已知条件可证明∠3=∠DFE，可证得结论．

【详解】

证明：（1）∵∠1+∠AFE=180°，∠1+∠BCF=180°，

∴∠AFE=∠BCF，

∴BC∥EF；

（2）∵∠BEG=∠EDF，

∴DF∥EH，

∴∠DFE=∠FEH，

又∵BC∥EF，

∴∠FEH=∠2，

又∵∠2=∠3，

∴∠DFE=∠3，

∴DF平分∠AFE．

【点睛】

本题主要考查平行线的判定和性质，掌握平行线的判定和性质是解题的关键，即①两直线平行⇔同位角相等，②两直线平行⇔内错角相等，③两直线平行⇔同旁内角互补，④a∥b，b∥c⇒a∥c．

20．将一副三角板按如图方式摆放，两个直角顶点重合，∠A=60°，∠E=∠B=45°．

（1）求证：∠ACE=∠BCD；

（2）猜想∠ACB与∠ECD数量关系并说明理由；

（3）按住三角板ACD不动，绕点C旋转三角板ECB，探究当∠ACB等于多少度时，AD∥CB．请在备用图中画出示意图并简要说明理由．

【答案】（1）证明见解析;（2）猜想：∠ACB+∠ECD=180°．理由见解析;（3）当∠ACB=120°或60°时，AD∥CB．理由理由见解析.

【解析】

试题分析：

（1）由∠ACD=∠BCE=90°，可得∠ACD-∠DCE=∠BCE-∠DCE，从而可得∠ACE=∠BCD；

（2）猜想：∠ACB+∠ECD=180°．由∠ACB+∠ECD=∠ACD+∠BCD+∠ECD=∠ACD+∠BCE=90°+90°=180°可得结论；

（3）如下图，因为∠A=60°，根据“同旁内角互补，两直线平行和内错角相等，两直线平行”可知，当∠ACB=120°，或∠ACB=60°时，AD∥BC.

试题解析：

（1）∵∠ACD=∠ECB=90°，

∴∠ACD﹣∠ECD=∠ECB﹣∠ECD，

即∠ACE=∠BCD．

（2）猜想：∠ACB+∠ECD=180°．理由如下：

∵∠ACB=∠ACD+∠DCB

∴∠ACB+∠ECD

=∠ACD+∠DCB+∠ECD

又∵∠DCB+∠ECD=∠ECB，

∴∠ACB+∠ECD=∠ACD+∠ECB=90°+90°=180°.

（3）当∠ACB=120°或60°时，AD∥CB．理由如下：

①如图1，根据“同旁内角互补，两直线平行”：

当∠A+∠ACB=180°时，AD∥BC，

此时，∠ACB=180°﹣∠A=180°﹣60°=120°．

②如图2，根据“内错角相等，两直线平行”：

当∠ACB=∠A=60°时，AD∥BC．

综上所述，当∠ACB=120°或60°时，AD∥BC.

点睛：在解第（3）小问时，利用手中的直角三角尺旋转演示一次，认真观察旋转过程，既能轻松找到解题思路，又能把两种情况都考虑到，从而完整的给出解答.

21．如图，已知点E在直线DC上，射线EF平分∠AED，过E点作EB⊥EF，G为射线EC上一点，连结BG，且．

（1）求证：；

（2）若，试判断AB与EF的位置关系，并说明理由．

【答案】（1）证明见解析；（2）AB∥EF，理由见解析．

【分析】

（1）根据垂直关系和平角的定义可得∠DEF+∠BEG=90°，又∠EBG+∠BEG=90°结论可证；

（2）由（1）和角平分线的定义可得∠A=∠AEF，再根据内错角相等，两直线平行即可证明．

【详解】

证明：（1）∵EB⊥EF,

∴∠FEB=90°，

∴∠DEF+∠BEG=180°-90°=90°，又∠EBG+∠BEG=90°

∴∠DEF=∠EBG

（2）AB∥EF，理由如下：

∵EF平分∠AED

∴∠AEF=∠DEF=

∵∠EBG=∠A，∠DEF=∠EBG，

∴∠A=∠AEF，

∴AB∥EF．

【点睛】

本题考查平行线的判定定理，同角（或等角）的余角相等，角平分线的有关证明．能根据同角（或等角）的余角相等完成角度之间的转化是解题关键．

22．已知：三角形ABC和同一平面内的点D．

（1）如图1，点D在BC边上，DE∥BA交AC于E，DF∥CA交AB于F．若∠EDF＝85°，则∠A的度数为_______°．

（2）如图2，点D在BC的延长线上，DF∥CA，∠EDF＝∠A，证明：DE∥BA．

（3）如图3，点D是三角形ABC外部的一个动点，过D作DE∥BA交直线AC于E，DF∥CA交直线AB于F，直接写出∠EDF与∠A的数量关系（不需证明）．

【答案】（1）85；（2）证明见解析；（3）∠EDF＝∠A或∠EDF+∠A＝180°．

【分析】

（1）根据平行线的性质，即可得到∠A＝∠EDF＝85°；

（2）延长BA交DF于G．根据平行线的性质以及判定进行推导即可；

（3）分两种情况讨论，即可得到∠EDF与∠A的数量关系：∠EDF＝∠A，∠EDF+∠A＝180°．

【详解】

解：（1）∵DE∥BA，DF∥CA，

∴∠A＝∠DEC，∠DEC＝∠EDF，

∵∠EDF＝85°

∴∠A＝∠EDF＝85°；

故答案为：85；

（2）证明：如图1，延长BA交DF于G．

∵DF∥CA，

∴∠2＝∠3．

又∵∠1＝∠2，

∴∠1＝∠3．

∴DE∥BA．

（3）∠EDF＝∠A或∠EDF+∠A＝180°，

理由：如图2，

∵DE∥BA，DF∥CA，

∴∠EDF+∠E＝180°，∠E+∠EAF＝180°，

∴∠EDF＝∠EAF＝∠A；

如图3，

∵DE∥BA，DF∥CA，

∴∠EDF+∠F＝180°，∠F＝∠CAB，

∴∠EDF+∠BAC＝180°．

即∠EDF+∠A＝180°，

【点睛】

本题主要考查了平行线的性质以及判定的运用，解题时注意：平行线的判定是由角的数量关系判断两直线的位置关系；平行线的性质是由平行关系来寻找角的数量关系．

23．解答题．

（1）如图，直线，相交于点O，，平分，且，请你求的度数．

（2）如图，已知，平分，，，求的度数．

【答案】（1）； （2）．

【分析】

（1）由已知条件和观察图形，根据垂直的定义、角平分线的定义和对顶角相等，利用这些关系可解此题．

（2）根据平行线的性质由CD∥AB得到∠BOC+∠DCO=180°，则∠BOC=120°，再根据角平分线定义得∠COF=∠BOC=60°，由EO⊥FO得∠EOF=90°，然后利用互余计算∠COF的度数．

【详解】

解：（1）∵，

∴，

∵，

∴，

∴

∴，

又∵平分，

∴∠，

∴．

（2）∵，

∴，

∴，

∵平分，

∴，

∵，

∴，

∴．

【点睛】

本题利用垂直的定义，角平分线的定义以及平行线的性质计算，要注意领会由垂直得直角两直线平行，同旁内角互补．

24．如图，已知直线，，E、F在上，且满足，平分．

（1）直线与有何位置关系？请说明理由．

（2）求的度数．

（3）若平行移动，在平行移动的过程中，存在使的情况，求的度数．

【答案】（1）直线与互相平行，理由见解析；（2）（3）存在，．

【分析】

（1）根据平行线的性质，以及等量代换证明，即可证得；

（2）由直线，根据两直线平行，同旁内角互补，即可求得的度数，又由，即可求得的度数．

（3）首先设，由直线，根据两直线平行，同旁内角互补与两直线平行，内错角相等，可求得与的度数，又由，即可得方程：，解此方程即可求得答案．

【详解】

解：（1）直线与互相平行，理由：

，

，

又

，

；

（2），

，

，平分，

；

（3）存在．

设．

，

；

，

，

．

若，

则，

得．

存在．

【点睛】

此题主要考查了平行线的性质与判定．解题的关键是注意掌握两直线平行，同旁内角互补与两直线平行，内错角相等定理的应用，注意数形结合与方程思想的应用．