期中综合检测03-2021-2022学年七年级数学下学期期中专项复习（人教版）

期中综合检测03

姓名：___________考号：___________分数：___________

（考试时间：100分钟  满分：120分）

一、 选择题（本大题共12小题，每小题3分，共36分。在每小题给出的四个选项中，只有一项是符合题目要求的）

1．图，C是直线AB上一点，CD⊥AB，EC⊥CF，则图中互余的角的对数与互补的角的对数分别是（   ）

A．3，4 B．4，7 C．4，4 D．4，5

【答案】B

【分析】

根据垂直的定义、角互余与互补的定义即可得．

【详解】

，

，

，，

，

，

，

，，

，

则图中互余的角的对数为4对；

，

，

点C是直线AB上一点，

，

，，

又，，

，，

则图中互补的角的对数为7对，

故选：B．

【点睛】

本题考查了垂直的定义、角互余与互补的定义，熟练掌握各定义是解题关键．

2．下列图形中，与是同位角的是（ ）

A． B．

C． D．

【答案】C

【分析】

根据同位角的定义可以判断对错 ．

【详解】

解：两条直线a、b被第三条直线c所截，在截线c的同旁，且在被截直线a、b同一侧的角称为同位角，根据这个定义，A选项的两角不在被截线的同侧，错误；B选项的两角不是两条直线被第三条直线所截形成的角，错误；C选项的角符合同位角的定义，正确；D选项的两角不是两条直线被第三条直线所截形成的角，错误．

故选C．

【点睛】

本题考查同位角的意义，通过同位角的意义进行灵活判断是解题关键．

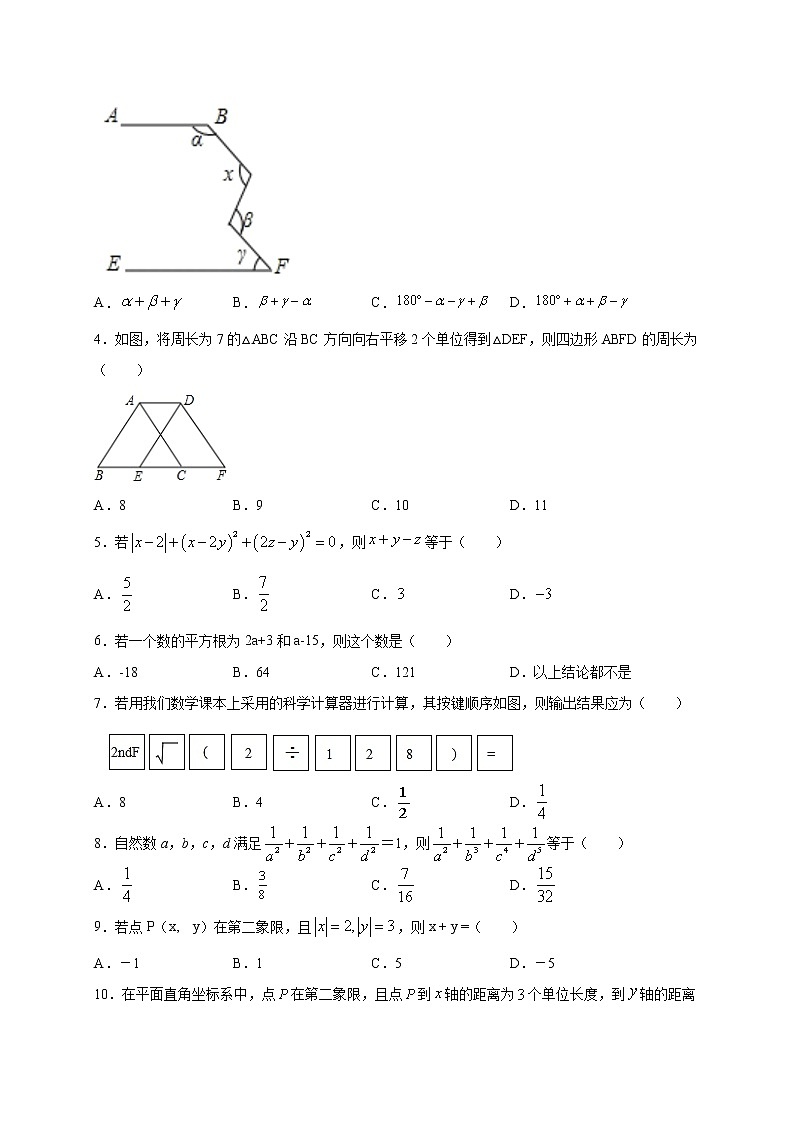
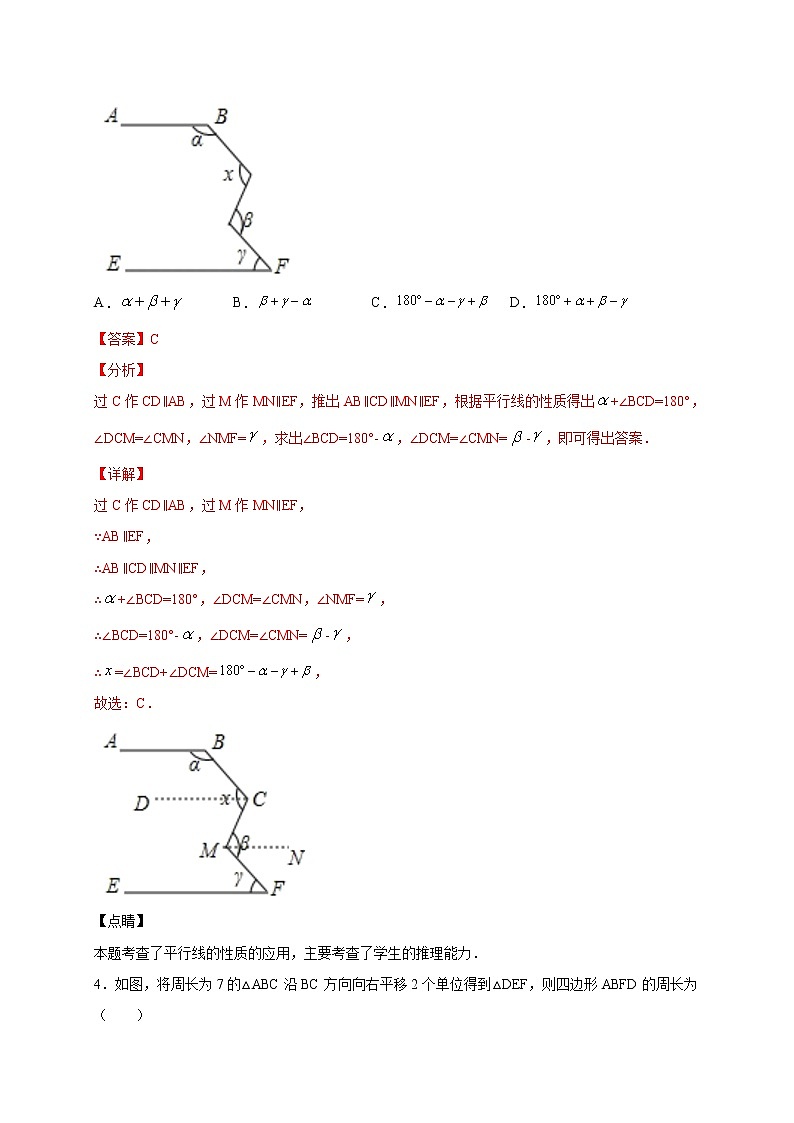
3．如图所示，若AB∥EF，用含、、的式子表示，应为（    ）

A． B． C． D．

【答案】C

【分析】

过C作CD∥AB，过M作MN∥EF，推出AB∥CD∥MN∥EF，根据平行线的性质得出+∠BCD=180°，∠DCM=∠CMN，∠NMF=，求出∠BCD=180°-，∠DCM=∠CMN=-，即可得出答案．

【详解】

过C作CD∥AB，过M作MN∥EF，

∵AB∥EF，

∴AB∥CD∥MN∥EF，

∴+∠BCD=180°，∠DCM=∠CMN，∠NMF=，

∴∠BCD=180°-，∠DCM=∠CMN=-，

∴=∠BCD+∠DCM=，

故选：C．

【点睛】

本题考查了平行线的性质的应用，主要考查了学生的推理能力．

4．如图，将周长为7的△ABC沿BC方向向右平移2个单位得到△DEF，则四边形ABFD的周长为（    ）

A．8 B．9 C．10 D．11

【答案】D

【分析】

根据平移的基本性质，得出四边形ABFD的周长=AD+AB+BF+DF=2+AB+BC+2+AC即可得出答案．

【详解】

解：根据题意，将周长为7的△ABC沿BC方向向右平移2个单位得到△DEF，
∴AD=2，BF=BC+CF=BC+2，DF=AC；
又∵AB+BC+AC=7，
∴四边形ABFD的周长=AD+AB+BF+DF=2+AB+BC+2+AC=11．
故选：D．

【点睛】

本题考查平移的基本性质：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．得到CF=AD，DF=AC是解题的关键．

5．若，则等于（    ）

A． B． C． D．

【答案】A

【分析】

根据非负数的性质列方程求出x、y、z的值，然后代入代数式进行计算即可得解．

【详解】

由题意得，x-2=0，x-2y=0，2z-y=0
解得x=2，y=1，z=,
所以，=2+1-=．
故选A．

【点睛】

此题考查非负数的性质，解题关键在于掌握几个非负数的和为0时，这几个非负数都为0．

6．若一个数的平方根为2a+3和a-15，则这个数是（    ）

A．-18 B．64 C．121 D．以上结论都不是

【答案】C

【分析】

根据正数有两个平方根，这两个平方根互为相反数，据此即可得到关于a的方程，从而可求得a的值，进而求得这个数．

【详解】

解：根据题意得：2a+3+（a-15）=0，
解得a=4，
则这个数是（2a+3）2=121．
故选：C．

【点睛】

本题主要考查了平方根的性质，正数的两个平方根互为相反数，据此把题目转化为解方程的问题，这是考试中经常出现的问题．

7．若用我们数学课本上采用的科学计算器进行计算，其按键顺序如图，则输出结果应为（    ）

A．8 B．4 C． D．

【答案】D

【分析】

根据2ndf键是功能转换键列算式，然后解答即可．

【详解】

解：依题意得：．

故选：D．

【点睛】

本题考查了利用计算器进行数的开方，是基础题，要注意2ndf键的功能．

8．自然数a，b，c，d满足＝1，则等于（　　）

A． B． C． D．

【答案】D

【分析】

只有a、b、c、d自然数都相等的时候，等式才成立，可得：a＝b＝c＝d＝2，即可求解．

【详解】

解:＝1，只有a、b、c、d自然数都相等的时候，等式才成立，

∴a＝b＝c＝d＝2；

．

故选：D．

【点睛】

本题考查新定义下的实数运算，熟练掌握“当且仅当a=b=c=d=2时，”是解题关键．

9．若点P（x,  y）在第二象限，且，则x + y =（　　）

A．－1 B．1 C．5 D．－5

【答案】B

【分析】

先根据第二象限点坐标符号特点可得，再化简绝对值可得x、y的值，然后代入即可得．

【详解】

点在第二象限，

，

又，

，

，

故选：B．

【点睛】

本题考查了第二象限点坐标符号特点、化简绝对值，熟练掌握第二象限点坐标符号特点是解题关键．

10．在平面直角坐标系中，点在第二象限，且点到轴的距离为个单位长度，到轴的距离为个单位长度，则点的坐标是（  ）

A． B． C． D．

【答案】C

【分析】

根据第二象限内点的横坐标是负数，纵坐标是正数，点到x轴的距离等于纵坐标的绝对值，到y轴的距离等于横坐标的绝对值解答．

【详解】

解：设

在第二象限，

到轴距离为，则

到轴距离为，则

故选

【点睛】

本题考查了点的坐标，熟记点到x轴的距离等于纵坐标的绝对值，到y轴的距离等于横坐标的绝对值是解题的关键．

11．在平面直角坐标系中，点A的坐标为（，），则点A在（    ）

A．第一象限 B．第二象限 C．第三象限 D．第四象限

【答案】D

【分析】

根据各象限内点的坐标特征解答．

【详解】

∵，

点A（，）在第四象限．
故选：D．

【点睛】

本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．

12．如图，在中，，，点的坐标为，点的坐标为，则点的坐标为（    ）

A． B． C． D．

【答案】A

【分析】

过点作轴的垂线交于点，过点作轴的垂线交于点，运用AAS证明得到，即可求得结论．

【详解】

解：过点作轴的垂线交于点，过点作轴的垂线交于点，

，

，

在和中，

，，

，

，，

，，

，

故选A．

二、填空题（本大题共6小题，每小题3分，共18分）

13．如图，现给出下列条件：①，②，③，④，⑤.其中能够得到AB//CD的条件是_______.(只填序号)

【答案】①②⑤

【分析】

根据平行线的判定定理对各小题进行逐一判断即可

【详解】

解：①∵∠1=∠B，∴AB∥CD，故本小题正确；
②∵∠2=∠5，∴AB∥CD，故本小题正确；
③∵∠3=∠4，∴AD∥BC，故本小题错误；
④∵∠1=∠D，∴AD∥BC，故本小题错误；
⑤∵∠B+∠BCD=180°，∴AB∥CD，故本小题正确．
故答案为①②⑤．

【点睛】

本题考查的是平行线的判定，熟知同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行是解答此题的关键．

14．如图所示，，点，，在直线上，点，在直线上，满足平分，，平分，若，那么___________．

【答案】146°

【分析】

根据平行线的性质和角平分线的性质，可以得到∠AEC的度数，本题得以解决．

【详解】

解：∵l1∥l2，

∴∠BAD+∠ABC=180°，

∵∠BAD=136°，

∴∠ABC=44°，

∵BD平分∠ABC，

∴∠DBC=22°，

∵BD⊥CD，

∴∠BDC=90°，

∴∠BCD=68°，

∵CE平分∠DCB，

∴∠ECB=34°，

∵l1∥l2，

∴∠AEC+∠ECB=180°，

∴∠AEC=146°，

故答案为：146°．

【点睛】

本题考查平行线的性质、角平分线的性质、垂线，解答本题的关键是明确题意，利用数形结合的思想解答．

15．方程的根是__________．

【答案】或．

【分析】

根据平方根的定义求解即可．

【详解】

解：，

两边开方得，或，

解得，或．

【点睛】

本题考查了平方根的意义，解题关键是熟练运用平方根的意义，准确进行计算．

16．a是的整数部分，b的立方根为-2，则a+b的值为________．

【答案】-5

【解析】

∵32<10<42,

∴的整数部分a=3,

∵b的立方根为-2,

∴b=-8,

∴a+b=-8+3=-5.

故答案是：-5.

17．已知点A坐标为，若直线轴，且，则点B坐标为________．

【答案】（1，7）或（1，﹣3）

【分析】

由直线轴可确定点B的横坐标为1，然后分当点B在点A上方和点B在点A下方两种情况，结合解答即可．

【详解】

解：∵直线轴，点A坐标为，

∴点B的横坐标为1，

∵，

∴当点B在点A上方时，点B的纵坐标为7，

当点B在点A下方时，点B的纵坐标为﹣3，

∴点B的坐标为（1，7）或（1，﹣3）．

故答案为：（1，7）或（1，﹣3）．

【点睛】

本题考查了图形与坐标，属于基础题目，正确分类、掌握解答的方法是解题关键．

18．已知点，轴，，则点的坐标为______．

【答案】(9，﹣2)或 (﹣3，﹣2)

【分析】

根据平行线的性质可得点M的纵坐标与点P的纵坐标相同，是﹣2，再根据MP＝6，即可求出点M的坐标．

【详解】

解：∵点P(3，−2)， MP//x轴，

∴点M的横坐标与点P的横坐标相同，是﹣2，

又∵MP＝6，

∴点M的横坐标为为3+6＝9，或3−6＝−3，

∴点M的坐标为 (9，﹣2)或 (﹣3，﹣2)．

故答案为：(9，﹣2)或 (﹣3，﹣2)．

三、解答题（本大题共6小题，共66分，解答应写出文字说明、演算步骤或推理过程）

19．如图，直线、相交于点，．

（）的余角是__________（填写所有符合要求的角）．

（）若，求的度数．

（3）若，求的度数.

【答案】（1）∠BOD、∠EOF、∠AOC； （2）∠BOF=110°；（3）∠COE=135°.

【解析】

试题分析：（1）先求得∠BOE和∠FOD为直角，然后依据余角的性质、对顶角的性质进行解答即可；

（2）先依据余角的性质得到∠EOF的度数，然后再由∠BOF＝∠FOE＋∠EOB求解即可；

（3）先根据∠BOE＝90°得出∠BOD＋∠DOE＝90°，由条件∠DOE＝∠BOD可得∠DOE＝∠BOD＝45°，然后根据∠COE＝180°－∠DOE计算即可得出答案．

试题解析：

解：（1）∵∠AOE＝90°，

∴∠EOB＝90°，

∴∠DOE与∠DOB互余．

∵∠AOC＝∠DOB，

∴∠AOC与∠EOD互余．

∵∠COF＝90°，

∴∠DOF＝90°，

∴∠DOE与∠EOF互余．

故答案为：∠BOD、∠EOF、∠AOC；

（2）∵∠DOF ＝90°，即∠DOE＋∠EOF＝90°，

∴∠EOF＝90°－∠DOE＝90°－70°＝20°，

∴∠BOF＝∠EOF＋∠EOB＝20°＋90°＝110°；

（3）∵∠AOE＝90°，∴∠BOE＝180°－∠AOE＝90°，即∠BOD＋∠DOE＝90°，

∵∠DOE＝∠BOD，∴∠DOE＝∠BOD＝45°，

∴∠COE＝180°－∠DOE＝135°.

点睛：本题主要考查的是余角的定义，对顶角的性质，熟练掌握相关知识是解题的关键．

20．如图，，，，点，，在同一条直线上．

（1）请说明与平行．

（2）若，求的度数．

【答案】（1）见解析；（2）45°

【分析】

（1）先根据AD⊥BE，BC⊥BE得出AD∥BC，故可得出∠ADE=∠C，再由∠A=∠C得出∠ADE=∠A，故可得出结论；

（2）由AB∥CD表示出∠C的度数，再由直角三角形的性质可得出结论．

【详解】

解：（1）∵AD⊥BE，BC⊥BE，

∴AD∥BC，

∴∠ADE=∠C．

∵∠A=∠C，

∴∠ADE=∠A，

∴AB∥CD；

（2）∵AB∥CD，∠ABC=3∠E，

∴∠C=180°-3∠E ，

∴∠E=90°-（180°-3∠E），

∴∠E=45°．

【点睛】

本题考查的是平行线的判定与性质，先根据题意得出AD∥BC是解答此题的关键．

21．化简求值.

（1）已知x，y为实数，且，求的值；

（2）已知，求的平方根.

【答案】（1）5；（2）

【解析】

【分析】

（1）利用二次根式有意义的条件求出x，y的值即可得解；

（2）先根据立方根的意义求出x的值，进而求出x+17的平方根即可.

【详解】

（1）∵

∵且，

∴，.

∴.

（2）∵，

∴，

∴，

∴，

的平方根是.

【点睛】

此题主要考查了二次根式有意义的条件以及立方根的意义，正确得出x，y的值是解题的关键.

22．若与互为相反数，求的值是多少？

【答案】-1

【分析】

根据互为相反数的性质和非负数的性质求得a，b的值，再进一步代入求解．

【详解】

∵与|a+b+1|互为相反数，

∴+|a+b+1|＝0，

∵≥0且|a+b+1|≥0，

∴a-b-3=0且a+b+1=0，

解得a=1，b=-2，

∴（a+b）5=（1-2）5=（-1）5=-1．

【点睛】

此题考查了非负数的性质、互为相反数的性质．几个非负数的和为0，则这几个非负数同时为0；互为相反数的两个数的和为0．

23．如图，一只蚂蚁从点沿数轴向右爬了2个单位长度到达点，点表示，设点所表示的数为．

（1）求的值；

（2）在数轴上还有、两点分别表示实数和，且有与互为相反数，求的平方根．

【答案】（1）2；（2）±4

【分析】

（1）先求出m＝2，进而化简|m＋1|＋|m−1|，即可；

（2）根据相反数和非负数的意义，列方程求出c、d的值，进而求出2c−3d的值，再求出2c−3d的平方根．

【详解】

（1）由题意得：m＝2，则m＋1＞0，m−1＜0，

∴|m＋1|＋|m−1|＝m＋1＋1−m＝2；

（2）∵与互为相反数，

∴+=0，

∴|2c＋d|＝0且＝0，

解得：c＝2，d＝−4，

∴2c−3d＝16，

∴2c−3d的平方根为±4．

【点睛】

本题主要考查数轴、相反数的定义，求绝对值，掌握求绝对值的法则以及绝对值与算术平方根的非负性，是解题的关键．

24．已知，在平面直角坐标系中，三角形ABC三个顶点的坐标分别为，，．请在所给的平面直角坐标系中按要求完成以下问题：

（1）画出三角形ABC；

（2）将三角形ABC先向下平移6个单位长度，再向左平移3个单位长度后得到的三角形（点，，分别是点A，B，C移动后的对应点）请画出三角形；并判断线段AC与位置与数量关系．

【答案】（1）作图见解析；（2）作图见解析；位置关系是：平行；数量关系是：相等．

【分析】

（1）根据点A、B、C三点的坐标在坐标系中描出各点，再顺次连接即可得；

（2）将三顶点分别向下平移6个单位长度，再向左平移3个单位长度后得到对应点，顺次连接可得，继而根据平移的性质解答可得．

【详解】

解：1）如图所示，△ABC即为所求；

（2）如图所示，A1B1C1即为所求，AC与A1C1平行且相等．

【点睛】

本题主要考查作图−平移变换，解题的关键是熟练掌握平移变换的定义和性质．