考点14 从统计图中获取信息专项练习-2021-2022学年七年级数学下册中考真题专项汇编之期末重难考点训练（人教版）

这是一份考点14 从统计图中获取信息专项练习-2021-2022学年七年级数学下册中考真题专项汇编之期末重难考点训练（人教版），文件包含考点14从统计图中获取信息专项练习解析版docx、考点14从统计图中获取信息专项练习原卷版docx等2份试卷配套教学资源，其中试卷共41页， 欢迎下载使用。

人教版2020——2021年七年级下册新题
从统计图中获取信息专项练习
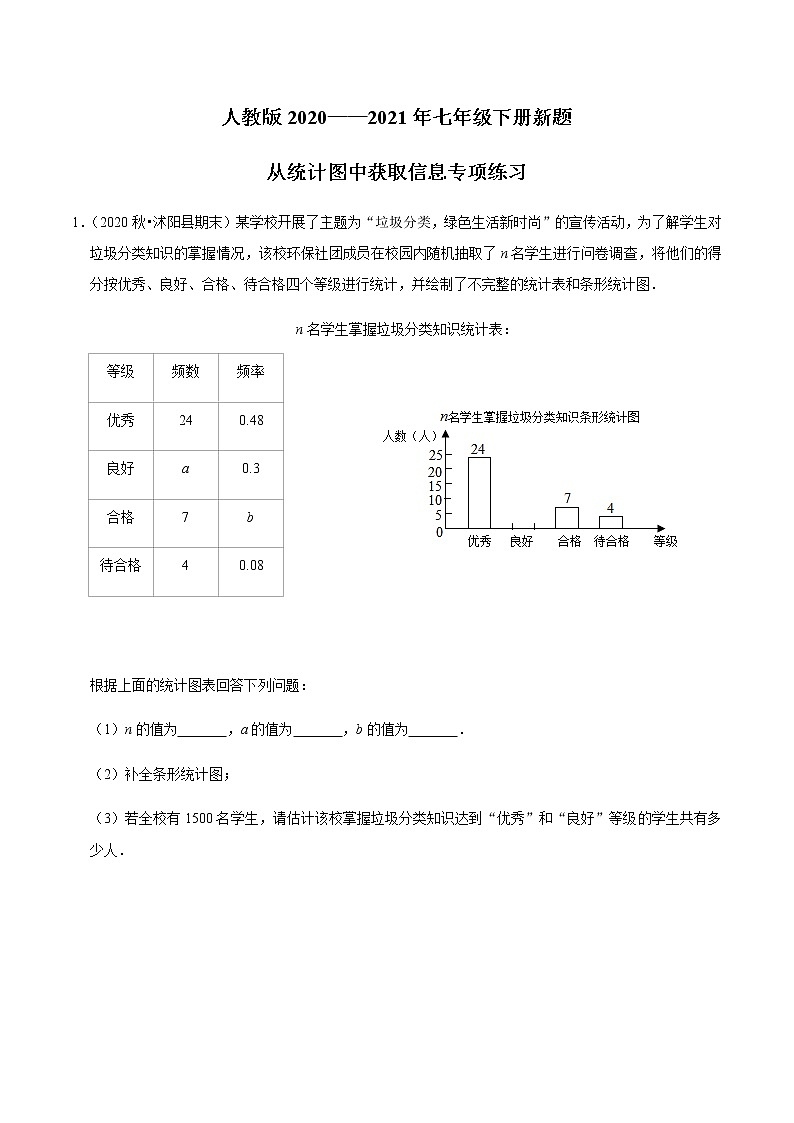
1．（2020秋•沭阳县期末）某学校开展了主题为“垃圾分类，绿色生活新时尚”的宣传活动，为了解学生对垃圾分类知识的掌握情况，该校环保社团成员在校园内随机抽取了n名学生进行问卷调查，将他们的得分按优秀、良好、合格、待合格四个等级进行统计，并绘制了不完整的统计表和条形统计图．
n名学生掌握垃圾分类知识统计表：
等级
频数
频率
优秀
24
0.48
良好
a
0.3
合格
7
b
待合格
4
0.08






根据上面的统计图表回答下列问题：
（1）n的值为　50　，a的值为　15　，b的值为　0.14　．
（2）补全条形统计图；
（3）若全校有1500名学生，请估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人．
【分析】（1）根据频率＝频数÷总数求解即可；
（2）根据以上所求数据即可补全条形图；
（3）用总人数乘以样本中优秀、良好的频率之和即可．
【解答】解：（1）n＝24÷0.48＝50，
a＝50×0.3＝15，b＝7÷50＝0.14，
故答案为：50，15，0.14；
（2）补全条形图如下：

（3）1500×（0.48+0.3）＝1170（人），
答：估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有1170人．
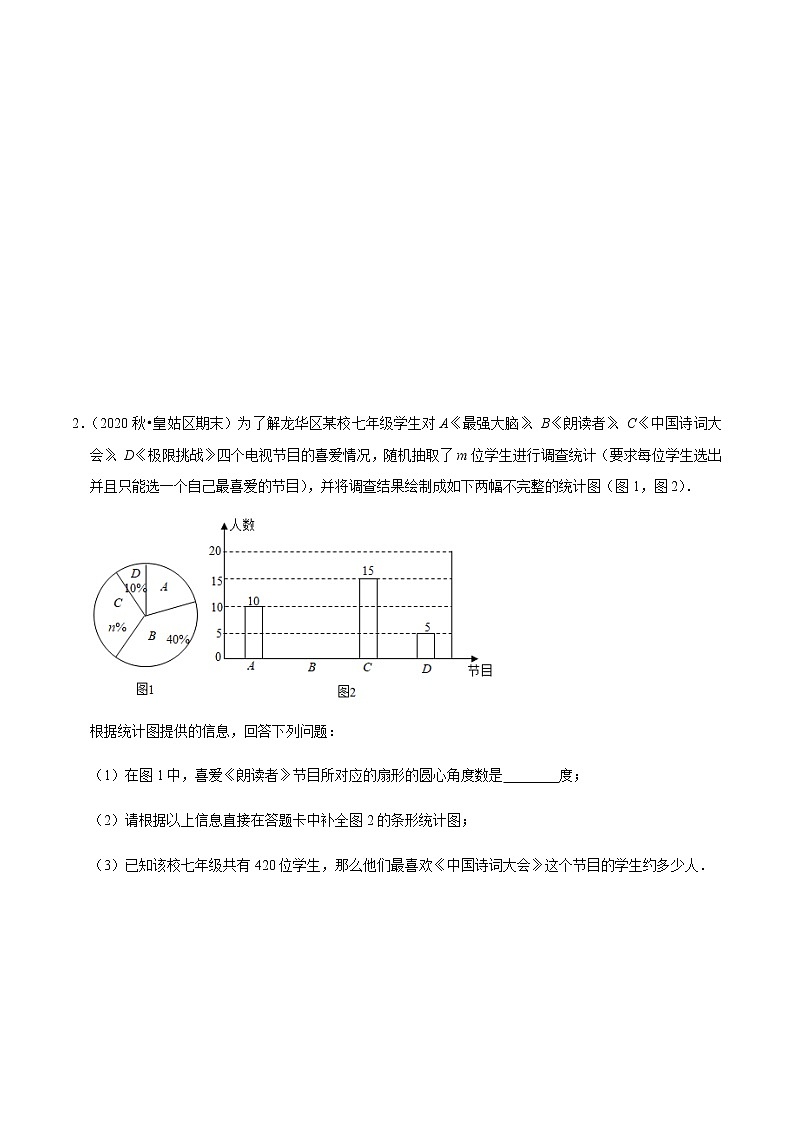
2．（2020秋•皇姑区期末）为了解龙华区某校七年级学生对A《最强大脑》、B《朗读者》、C《中国诗词大会》、D《极限挑战》四个电视节目的喜爱情况，随机抽取了m位学生进行调查统计（要求每位学生选出并且只能选一个自己最喜爱的节目），并将调查结果绘制成如下两幅不完整的统计图（图1，图2）．

根据统计图提供的信息，回答下列问题：
（1）在图1中，喜爱《朗读者》节目所对应的扇形的圆心角度数是　144　度；
（2）请根据以上信息直接在答题卡中补全图2的条形统计图；
（3）已知该校七年级共有420位学生，那么他们最喜欢《中国诗词大会》这个节目的学生约多少人．
【分析】（1）用360°乘以喜爱《朗读者》节目的人数所占的百分比即可；
（2）从两个统计图中可知，D组的人数为5人，占调查人数的10%，求出调查的总人数，再用总人数减去其他人数，求出喜欢B的人数，从而补全统计图；
（3）用总人数乘以C组所占的百分比即可得出答案．
【解答】解：（1）喜爱《朗读者》节目所对应的扇形的圆心角度数是：360°×40%＝144°．
故答案为：144；
（2）调查的总人数有：＝50（人），
喜爱B的人数有：50﹣10﹣15﹣5＝20（人），
补全统计图如下：

（3）他们最喜欢《中国诗词大会》这个节目的学生有420×＝126（人）．
3．（2020秋•沙坪坝区期末）某校为进一步落实“素质教育”，决定在七、八两个年级开展面塑、刺绣、雕刻、川剧等四项特色选修课，每个学生必选且只能选一项．学校为了解选择各种特色选修课的学生人数，随机抽取了部分学生进行调查，并绘制出以下两幅不完整的统计图，请根据统计图回答下列问题：
（1）这次活动一共调查了多少名学生？
（2）补全条形统计图；
（3）若该校七、八两个年级的总人数是800人，请估计选择雕刻项目的学生人数．

【分析】（1）从两个统计图可知，“面塑”的频数为14人，占调查人数的35%，可求出调查人数；
（2）求出“雕刻”的频数即可补全条形统计图；
（3）求出“雕刻”所占得百分比即可．
【解答】解：（1）14÷35%＝40（名），
答：这次活动一共调查了40名学生；
（2）选择“雕刻”的有40﹣14﹣2﹣8＝16（人），
补全的条形统计图如图所示：

（3）（人），
即该选择雕刻项目的学生约有320人．

4．（2020秋•桂林期末）为了解某校七年级学生体质健康测试项目中的“坐位体前屈”情况，随机抽取该年级部分学生进行了一次“坐位体前屈”测试，并根据标准把测试成绩分成A，B，C，D个等级，绘制出不完整的统计图：

请根据图中信息解答下列问题：
（1）本次抽取参加测试的学生共　50　人，扇形统计图中B等级占的百分比是　40%　；
（2）补全条形统计图；
（3）若规定“坐位体前屈”测试成绩为D等级属于不合格，那么本次抽取的测试中，合格率是多少？
【分析】（1）由A类别的人数及其所占百分比可得总人数，用360°乘以B类别的百分比即可得出答案；
（2）由各类别人数之和等于总人数求得C的人数，从而补全图形；
（3）用ABC等级的人数之和除以总人数即可得出答案．
【解答】解：（1）本次抽取参加测试的学生共有：15÷30%＝50（人），
扇形统计图中B等级占的百分比是×100%＝40%．
故答案为：50，40%；

（2）C类的人数为50﹣（15+20+5）＝10（人），
补全统计图如下：

（3） 本次抽取的测试中，合格率是×100%＝90%．

5．（2020秋•永定区期末）某校准备开展艺术节活动，设了四个比赛项目，它们分别是演讲，唱歌，书法，绘画．要求每位同学必须参加，且限报一项活动．随机抽取了部分学生的选项进行统计，并将统计结果绘成两幅统计图．请你结合图示所给出的信息解答下列问题．

（1）本次共调查了多少名学生？
（2）求出扇形统计图中参加书法比赛的学生所在扇形圆心角的度数？
（3）若该校有500名学生，请你估计这次艺术活动中，参加绘画的学生有多少人？
【分析】（1）根据唱歌的人数和所占的百分比求出总人数即可；
（2）利用对应的百分比乘以360度即可求解；
（3）利用总人数500乘以对应的百分比即可求解．
【解答】解：（1）本次共调查的学生总数是：×100%＝50（人）．
（2）参加书法比赛的学生所占的比例是20%，
则扇形的圆心角的度数是：360×20%＝72°；
（3）参加绘画比赛的人数是：500×12%＝60（人）．
6．（2020秋•丘北县期末）受疫情影响，国家推出了“网络授课”，使得初中学生越来越离不开手机，“沉迷手机”现象再次受到社会的关注，记者小王随机调查了某小区若干名学生和家长对中学生配带手机的看法，统计整理并作了如图统计图：

根据统计图中提供的信息，解答下列问题：
（1）求本次调查的家长总人数；
（2）补全条形统计图，并求出家长“反对”带手机所占扇形圆心角的度数；
（3）估计该小区1200名学生中“反对”配带手机的学生人数．
【分析】（1）利用条形图以及扇形统计图得出总人数即可；
（2）用总人数减去其他人数，求出家长反对带手机人数，再补全统计图即可；
用360°乘以家长“反对”带手机所占的百分比即可得出扇形圆心角的度数；
（3）用总人数乘以“反对”配带手机的学生所占的百分比即可．
【解答】解：（1）调查家长总人数：80÷20%＝400（人）；
（2）家长反对带手机人数：400﹣40﹣80＝280（人），
补全统计图如图所示：

圆心角度数：×360°＝252°；
（3）1200×＝180（人），
答：该小区1200名学生中“反对”配带手机的学生人数是180人．
7．（2020秋•锡山区期末）某校随机抽取部分学生，对“学习习惯”进行问卷调查．设计的问题：对自己做错的题目进行整理、分析、改正；答案选项为：A．很少；B．有时；C．常常；D．总是．将调查结果的数据进行了整理、绘制成如图两幅不完整的统计图．

请根据图中信息，解答下列问题：
（1）填空：a＝　12　%，b＝　36　%；
（2）请你补全条形统计图；
（3）若该校有2000名学生，请你估计其中“常常”和“总是”对错题进行整理、分析、改正的学生各有多少名？
【分析】（1）首先计算出抽查的学生总数，然后再计算a、b的值即可；
（2）计算出“常常”所对的人数，然后补全统计图即可；
（3）利用样本估计总体的方法计算即可．
【解答】解：（1）调查总人数：44÷22%＝200（人），
a＝×100%＝12%，
b＝×100%＝36%，
故答案为：12，36；
（2）“常常”所对的人数：200×30%＝60（人），
补全统计图如图所示：
；
（3）2000×30%＝600（人），
2000×36%＝720（人），
答：“常常”对错题进行整理、分析、改正的有600人，“总是”对错题进行整理、分析、改正的有720人．
8．（2020秋•德江县期末）为了了解学校图书馆上个月借阅情况，管理老师从学生对艺术、经济、科普及生活四类图书借阅情况进行了统计，并绘制了下列不完整的统计图，请根据图中信息解答下列问题：

（1）上个月借阅图书的学生有多少人？扇形统计图中“经济”部分的圆心角度数是多少？
（2）把条形统计图补充完整；
（3）从借阅情况分析，如果要添置这四类图书3600册，请你估算“科普”类图书应添置多少册合适？
【分析】（1）用借“生活”类的书的人数除以它所占的百分比即可得到调查的总人数；然后用360°乘以借阅“经济“的人数所占的百分比得到“经济”部分的圆心角度；
（2）先计算出借阅“科普“的学生数，然后补全条形统计图；
（3）利用样本估计总体，用样本中“科普”类所占的百分比乘以3600即可．
【解答】解：（1）上个月借阅图书的学生总人数为60÷25%＝240（人）；
扇形统计图中“经济”部分的圆心角度数为360°×＝60°．
（2）借阅“科普”类图书的学生数为240﹣100﹣60﹣40＝40（人），
条形统计图如图所示：

（3）3600×＝600（册），
答：估计“科普”类图书应添置600册合适．
9．（2020秋•中方县期末）网瘾低龄化问题已引起社会各界的高度关注．有关部门在全国范围内对12～35岁的网瘾人群进行简单随机抽样调查并得到如图，期中30～35岁的网瘾人数占样本人数的20%．
（1）请把图中缺失的数据、图形补充完整；
（2）若12～35岁网瘾人数约为4000人，请你根据图中数据估计网瘾人群中12～17岁的网瘾人数．

【分析】（1）先求出被调查的总人数，再根据四个年龄段的人数之和等于总人数求出12～17岁的人数，从而补全图形；
（2）先求出12～17岁人数所占百分比，再用总人数乘以所求百分比即可．
【解答】解：（1）∵被调查的总人数为480÷20%＝2400（人），
∴12～17岁的人数为2400﹣600﹣576﹣480＝744（人），
补全图形如下：

（2）744÷2400×100%＝31%，
4000×31%＝1240（人），
∴若12～35岁网瘾人数约为4000人，则根据图中数据估计网瘾人群中12～17岁的网瘾人数是1240．
10．（2020秋•娄星区期末）某区为了了解初中学生毕业后的就读意向，对该区九年级部分学生进行了一次抽样调查，调查表设计有四个选项：A．只愿意就读普通高中；B．只愿意就读中等职业技术学校；C．就读普通高中或中等职业技术学校都愿意；D．其它．将调查数据进行了整理，并绘制了尚不完整的两幅统计图，请根据相关信息，解答下列问题：

（1）本次活动共调查了多少名学生？
（2）补全图①，并求出图②中A区域的圆心角的度数；
（3）若该区九年级学生共有8000名，请估算该区九年级学生中只愿意就读普通高中的人数是多少？
【分析】（1）根据C的人数和圆心角的度数即可得出本次活动共调查的总人数；
（2）用总人数乘以B所占的百分比，求出B的人数，再用总人数减去其他人数求出D的人数，然后补全统计图即可；用360°乘以A区域所占的百分比求出A区域的圆心角的度数；
（3）用该区九年级的总人数乘以只愿意就读普通高中的人数所占的百分比即可．
【解答】解：（1）80÷＝800（人），
答：本次活动共调查了800名学生．
（2）B区域：800×25%＝200（人），
D区域：800﹣480﹣200﹣80＝40（人），
补全的统计图如下：

A区域的圆心角的度数为：×360°＝216°；
（3）8000×＝4800（人），
答：该区九年级学生中只愿意就读普通高中的人数为4800人．
11．（2020秋•阿城区期末）以人工智能、大数据、物联网为基础的技术创新促进了新业态蓬勃发展，新业态发展对人才的需求更加旺盛．某大型科技公司上半年新招聘软件、硬件、总线、测试四类专业的毕业生，现随机的抽取了部分新聘毕业生的专业情况进行调查，并将调查结果绘制成两幅不完整的统计图，根据已知信息，解答下列问题：

（1）求本次共抽查了多少名新聘毕业生；
（2）请补全形统计图；
（3）该公司新聘600名毕业生，请你估计“软件”专业的毕业生有多少名．
【分析】（1）根据总线的人数和所占的百分比求解可得答案；
（2）求得硬件专业的毕业生，从而可以将条形统计图补充完整；
（3）根据统计图中的数据，可以计算出“软件”专业的毕业生的人数．
【解答】解：（1）15÷30%＝50，
∴本次共抽查了50名新聘毕业生；
（2）硬件专业的毕业生有：50×40%＝20（人），
补全的条形统计图如图所示；

（3）600×＝120（名），
答：估计“软件”专业的毕业生有120名．
12．（2020秋•万山区期末）全国脱贫攻坚工作已经基本结束，下一步将全面进入乡村振兴，各项惠农政策会有一定的变化．某村为了了解政策的宣传情况，对村民进行了随机抽样调查，根据村民对政策的了解程度由高到低分为A，B，C，D四个等级，并对调查结果分析后绘制了如下两幅不完整的统计图，请你根据图中提供的信息完成下列问题：

（1）求被调查村民的人数，并将条形统计图补充完整；
（2）求扇形统计图中的A等级对应的扇形圆心角的度数；
（3）已知该村有1500名村民，估计该村村民对政策内容了解程度达到A等级的村民有多少人？
【分析】（1）根据B等级的人数和所占的百分比，求出总人数，再用总人数乘以C所占的百分比，求出C等级的人数，再用总人数减去其它等级的人数，求出C等级的人数，从而补全统计图；
（2）用360°乘以A等级所占的百分比即可；
（3）用该村的总人数乘以了解程度达到A等级的村民所占的百分比即可．
【解答】解：（1）被调查村民的人数是：48÷40%＝120（人），
C等级的人数有：120×15%＝18（人），
A等级的人数有：120﹣48﹣18﹣12＝42（人）．
补充条形统计图如图：

（2）扇形统计图中的A等级对应的扇形圆心角为×360°＝126°．
（3）1500×＝525（人）．
答：该校学生对政策内容了解程度达到A等级的学生约有525人．
13．（2020秋•鹤城区期末）某校为了解九年级男同学的中考体育考试准备情况，随机抽取部分男同学进行了1000米跑步测试．按照成绩分为优秀、良好、合格与不合格四个等级，学校绘制了如下不完整的统计图．

（1）根据给出的信息，补全两幅统计图；
（2）该校九年级有600名男生，请估计成绩未达到良好有多少名？
【分析】（1）先利用良好等级的人数除以它所占的百分比得到调查的总人数，再计算出合格等级的人数，然后分别计算出合格等级人数所占的百分比和优秀等级人数所占的百分比后补全两个统计图；
（2）用600乘以合格与不合格两个等级的百分比的和可估计成绩未达到良好等级的人数；
【解答】解：（1）抽取的学生数：16÷40%＝40（人）；
抽取的学生中合格的人数：40﹣12﹣16﹣4＝8，
合格所占百分比：8÷40×100%＝20%，
优秀人数：12÷40×100%＝30%，
如图所示：


（2）成绩未达到良好的男生所占比例为：20%+10%＝30%，
所以估计成绩未达到良好有600×30%＝180（名）．

14．（2020秋•成都期末）加强劳动教育是学校贯彻“五育并举”的重要举措．为了解学生参加各项劳动的情况，某校对七年级部分学生进行了随机问卷调查，其中一个问题是“你每周在家参加家务劳动的时间是多少？”，共有如下四个选项：
A.1小时以下
B.1～2小时（不包含2小时）
C.2～3小时（包含2小时）
D.3小时以上
图①、图②是根据调查结果绘制的两幅不完整的统计图，请你根据统计图提供的信息解答以下问题：
（1）填空：本次问卷调查一共调查了　200　名学生；
（2）请将图①的条形统计图补充完整，并求出图②中D部分所对应的圆心角度数；
（3）若该校共有1800名学生，请你估计全校可能有多少名学生每周在家参加家务劳动的时间在2小时以上（包含2小时）？
【分析】（1）根据B选项人数及其占被调查人数的比例计算即可得出答案．
（2）用总人数减去其他选项的人数求出D选项的人数，即可补全统计图；用360°乘以D部分所占的百分比即可得出D部分所对应的圆心角度数；
（3）用该校的总人数乘以每周在家参加家务劳动的时间在2小时以上（包含2小时）的人数所占的百分比即可．
【解答】解：（1）本次问卷调查一共调查的学生数是：100÷50%＝200（名）．
故答案为：200；
（2）劳动的时间在3小时以上的人数有：200﹣60﹣100﹣30＝10（名），补全统计图如下：

D部分所对应的圆心角度数是360°×＝18°；
（3）根据题意得：
1800×＝360（名），
答：
估计全校可能有360名学生每周在家参加家务劳动的时间在2小时以上（包含2小时）．
15．（2020秋•岳阳期末）某中学的一个数学兴趣小组在本校学生中开展主题为“垃圾分类知多少”的专题调查活动，采取随机抽样的方式进行问卷调查．问卷调查的结果分为A．“非常了解”、B．“比较了解”、C．“基本了解”、D．“不太了解”四个等级，划分等级后的数据整理成如下表格和频数分布直方图．
等级
频数
频率
非常了解
30
b
比较了解

0.25
基本了解
100
0.5
不太了解
20

合计
a
1

根据以上信息，请回答下列问题：
（1）表中a＝　200　，b＝　0.15　；
（2）请补全频数分布直方图；
（3）若该校有学生1800人，请根据调查结果估计这些学生中“不太了解”垃圾分类知识的人数．
【分析】（1）先根据“基本了解”的人数及其对应频率求出总人数a的值，再根据频率＝频数÷总人数即可求出a的值；
（2）根据以上所求结果即可补全图形；
（3）用总人数乘以样本中这些学生中“不太了解”垃圾分类知识对应的频率即可．
【解答】解：（1）∵被调查的总人数a＝100÷0.5＝200（人），
∴b＝30÷200＝0.15，
故答案为：200，0.15；
（2）补全频数分布直方图如下：

（3）1800×（1﹣0.15﹣0.25﹣0.5）＝180（人）．
答：估计这些学生中“不太了解”垃圾分类知识的人数为180人．
16．（2020秋•涟源市期末）在“弘扬传统文化，打造书香校园”活动中，学校计划开展四项活动：“A国学诵读”、“B演讲”、“C课本剧”、“D书法”．要求每位同学必须且只能参加其中一项活动，学校为了了解学生的意愿，随机调查了部分学生，结果统计如图所示：

（1）求被调查的总人数；
（2）扇形统计图中，活动D所占圆心角为多少度？
（3）请补全条形统计图．
【分析】（1）根据参加活动C的人数和所占的百分比，可以求得本次调查的总人数；
（2）根据（1）中的结果和扇形统计图中的数据，可以计算出参加活动B的人数，然后即可得到参加活动D的人数，从而可以计算出活动D所占圆心角为多少度；
（3）根据（2）中参加活动B和D的人数，可以将条形统计图补充完整．
【解答】解：（1）由统计图可得，
被调查的同学有：12÷20%＝60（人），
即被调查的一共有60人；
（2）∵参加活动B的有60×15%＝9（人），
∴参加活动D的有60﹣（27+9+12）＝12（人），
，
即扇形统计图中，活动D所占圆心角为72°；
（3）由（2）知：
参加活动B的有9人，参加活动D的有12人，
补全的条形统计图如右图所示．

17．（2020秋•武侯区期末）为了倡导公筷公勺和分餐制为主的餐桌文明，某校开展了“你的家庭就餐分餐了吗？”的调查活动，随机抽取了部分学生，对他们家庭就餐的分餐情况进行调查，调查结果有四种：A完全分餐，B多数时候分餐，C偶尔分餐，D从来不分餐，学校根据调查的数据进行整理，绘制了两幅不完整的统计图．

根据以上信息，解答下列问题：
（1）求本次调查的学生总人数，并补全条形统计图；
（2）求扇形统计图中C对应的扇形的圆心角的度数；
（3）若该校共有学生2400人，在（1）的基础上估计该校家庭就餐的分餐情况为“多数时候分餐”的学生人数．
【分析】（1）根据D的人数和所占的百分比求出总人数，再用总人数减去其它分餐情况的人数，求出多数时候分餐的人数，从而补全统计图；
（2）用360°乘以C所占的百分比即可；
（3）用总人数乘以“多数时候分餐”的学生人数所占的百分比即可．
【解答】解：（1）本次调查的学生总人数是150÷25%＝600（人），
多数时候分餐的人数有：600﹣40﹣210﹣150＝200（人），补全统计图如下：

（2）扇形统计图中C对应的扇形的圆心角的度数是360°×＝126°；
（3）根据题意得：
2400×＝800（人），
答：该校家庭就餐的分餐情况为“多数时候分餐”的学生人数有800人．
18．（2020秋•东安县期末）我县某校为了让学生的课余生活丰富多彩，开展了以下课外活动：
A学习兴趣小组、B健身体育活动、C美术绘画、D音乐、E其他
为了解学生的选择情况，现从该校随机抽取了部分学生进行问卷调查（参与问卷调查的每名学生只能选择其中一项），并根据调查得到的数据绘制了如图所示的两幅不完整的统计图．请根据统计图提供的信息回答下列问题（要求写出简要的解答过程）．
（1）此次共调查了　200　名学生；
（2）将条形统计图补充完整；
（3）“健身体育活动”所在扇形的圆心角的度数为　108°　；
（4）若该校共有4000名学生，请估计该校喜欢A，B，C三类活动的学生共有多少人？

【分析】（1）由A类型人数及其所占百分比可得总人数；
（2）总人数乘以D的百分比求得其人数，再根据各类型人数之和等于总人数求得B的人数，据此可补全图形；
（3）用360°乘以B类型人数所占比例；
（4）总人数乘以前三项人数之和所占比例即可得．
【解答】解：（1）此次调查的总人数为40÷20%＝200（人），
故答案为：200；
（2）D类型人数为200×25%＝50（人），
B类型人数为200﹣（40+30+50+20）＝60（人），
补全图形如下：

（3）“健身体育活动”所在扇形的圆心角的度数为360°×＝108°，
故答案为：108°；
（4）估计该校喜欢A、B、C三类活动的学生共有4000×＝2600（人）．
19．（2020秋•覃塘区期末）某校在“校艺术节”期间，举办了A演讲、B唱歌、C书法、D绘画共四个项目的比赛．要求每位同学必须参加且限报一项．以九年级（一）班为样本进行统计，并将结果绘制尚不完整的条形和扇形统计图，请根据统计图解答下列问题：

（1）在扇形统计图中，D项的百分率是　4%　；
（2）在扇形统计图中，C项的圆心角的度数是　72°　；
（3）请补充完整条形统计图；
（4）若该校九年级有500名学生，那么九年级参加演讲和唱歌比赛的学生共有多少人？
【分析】（1）根据A的人数及其百分比得出总人数，绘画人数除50即可．
（2）两图结合，按频数和频率的关系知c＝20%，由此即可求出相应圆心角的度数；
（3）总人数减去其余各组人数得出C组人数，即可补全图形；
（3）利用样本估计总体即可．
【解答】解：（1）∵参加比赛的总人数为13÷26%＝50（人），
∴参加绘画比赛的学生人数占全班总人数的百分比是 ×100%＝4%；
故答案为：4%；
（2）根据题意得：
360°×（1﹣26%﹣50%﹣4%）＝72°．
则参加书法比赛的C项所在的扇形圆心角的度数是72°．
故答案为：72°；
（3）参加书法的人数为50﹣（13+25+2）＝10（人），补全图象如下：


（4）500×（50%+26%）＝380，
答：九年级参加演讲和唱歌比赛的学生约有380人．
20．（2020秋•醴陵市期末）对垃圾进行分类投放，能有效提高对垃圾的处理和再利用，减少污染，保护环境．为了调查同学们对垃圾分类知识的了解程度，增强同学们的环保意识，普及垃圾分类及投放的相关知识，某校数学兴趣小组的同学设计了“垃圾分类知识及投放情况”问卷，并在本校随机抽取部分同学进行问卷测试，把测试成绩分成“优、良、中、差”四个等级，绘制了不完整的统计图：

根据以上统计信息，解答下列问题：
（1）求成绩是“优”的人数占抽取人数的百分比；
（2）求本次随机抽取问卷测试的人数；
（3）请把条形统计图补充完整；
（4）若该校学生人数为4000人，请估计成绩是“优”和“良”的学生共有多少人？
【分析】（1）用成绩是“优”所在扇形圆心角的度数除以360°即可；
（2）用成绩是“优”的人数除以所占的百分比即可；
（3）利用总人数减去其它组的人数即可求得成绩是“中”的人数，从而补全条形图；
（4）利用总人数4000乘以成绩是“优”和“良”的学生所占的百分比即可．
【解答】解：（1）成绩是“优”的人数占抽取人数的百分比是：＝20%；
（2）本次随机抽取问卷测试的人数是：40÷20%＝200（人）；
（3）成绩是“中”的人数是200﹣（40+70+30）＝60（人），
条形统计图补充如下：

（4）4000×＝2200（人），
答：成绩是“优”和“良”的学生共有2200人．