人教A版 (2019)必修 第二册6.4 平面向量的应用教课ppt课件

这是一份人教A版 (2019)必修 第二册6.4 平面向量的应用教课ppt课件，共19页。PPT课件主要包含了一余弦定理，解析法，由余弦定理变形得，这就是勾股定理，钝角三角形，直角三角形，锐角三角形，当A为三角形的最大角，用于判定三角形形状，解由余弦定理得等内容，欢迎下载使用。
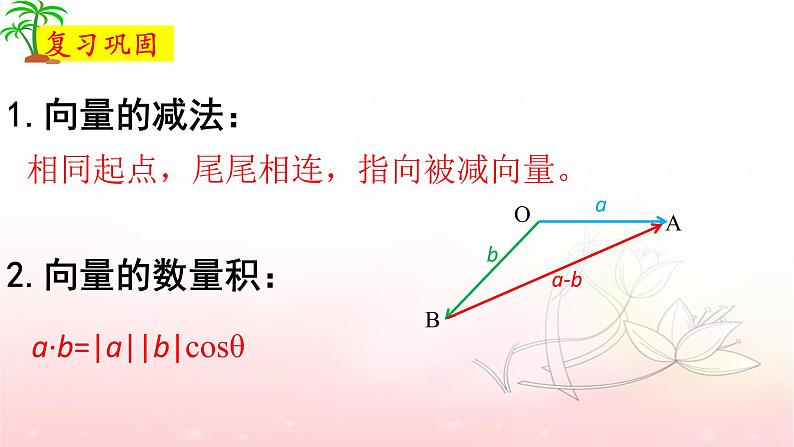
1.向量的减法：2.向量的数量积：
相同起点，尾尾相连，指向被减向量。
a·b=|a||b|csθ
一个三角形含有各种各样的几何量，例如三边边长、三个内角的度数、面积等，它们 之间存在着确定的关系.例如，在初中，我们得到过勾股定理、锐角三角函数，这是直角 三角形中的边、角定量关系.对于一般三角形，我们已经定性地研究过三角形的边、角关 系，得到了 SSS, SAS, ASA, AAS等判定三角形全等的方法.这些判定方法表明，给 定三角形的三个角、三条边这六个元素中的某些元素，这个三角形就是唯一确定的.那么 三角形的其他元素与给定的某些元素有怎样的数量关系？
　　三角形任一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍．
应用题型：已知两边和一个夹角，求第三边问题．
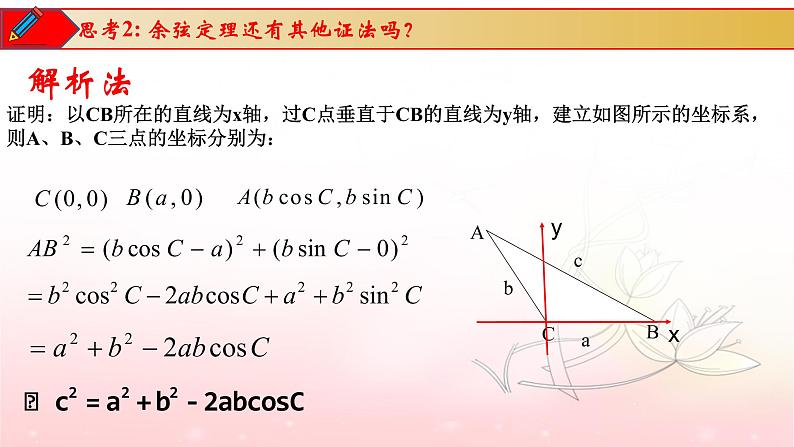
证明：以CB所在的直线为x轴，过C点垂直于CB的直线为y轴，建立如图所示的坐标系，则A、B、C三点的坐标分别为：
应用题型：已知三条边求角问题．
从余弦定理及其推论可以看出，三角函数把几何中关于三角形的定性结论变成了可定 量计算的公式.
如果△ABC中有一个角是直角，例如，A= 90°,这时csA = 0.由余弦定理可得
由此可见，余弦定理是勾股定理的推广，而勾股定理是余 弦定理的特例.
剖 析 定 理
问题1：公式有怎样的结构特征？
（1）轮换对称，简洁优美;
（2）每个等式中有同一个三角形中的四个元素，知三求一.（方程思想）
（1）已知三边 求三个角 SSS
问题2：余弦定理在解三角形中的作用是什么？
（2）已知两边和它们的夹角，求第三边和其他两个角. SAS
已知a、b、c（三边），可以求什么？
剖 析 定 理
一般地，三角形的三个角A，B，C和它们的对边a，b，c叫做三角形的元素，已知三角形的几个元素求其它元素的过程叫做解三角形。
例5.在 中，已知b=60cm，c=34cm， ，解这个三角形（角度精准到 ，边长精确到1cm.
例6.在 中，已知a=7，b=8，锐角C满足 ，求B（ 精准到 )
解：因为 ，且C为锐角。
1、已知两边和夹角求第三边。