2021学年4 圆周角和圆心角的关系授课课件ppt

3.4.2圆周角和圆心角的关系-学案

一．学习目标

1.掌握直径（或半圆）所对的圆周角是直角及90°的圆周角所对的弦是直径的性质，

2．掌握圆内接四边形概念与性质

3．能运用上述性质解决问题.           

二．温故知新

  1．如图1，点A、B、C、D在⊙O上，若∠BAC=40°，则

（1）∠BOC=       °,理由是                ；

（1）∠BDC=       °,理由是                .

（1）     （2）

2.如图2，在△ABC中，OA=OB=OC,则∠ACB=      °. 

三、自主探究：阅读课本p81— 83   

探究（一）圆周角定理的推论：

1.如图,BC是⊙O的直径,它所对的圆周角是锐角、钝角，还是直角？为什么？

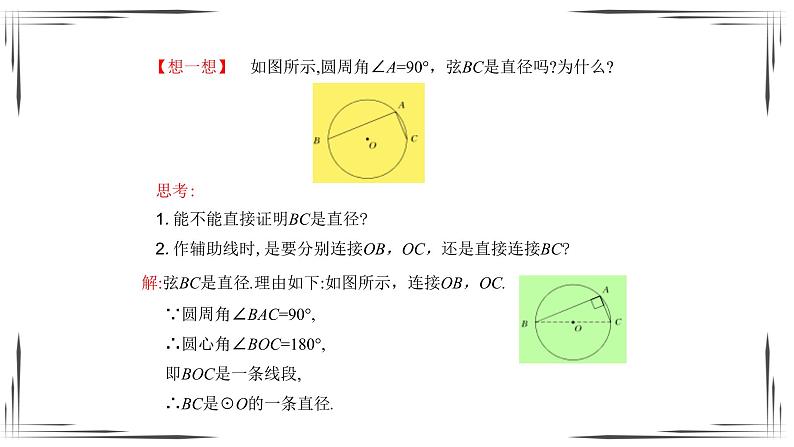
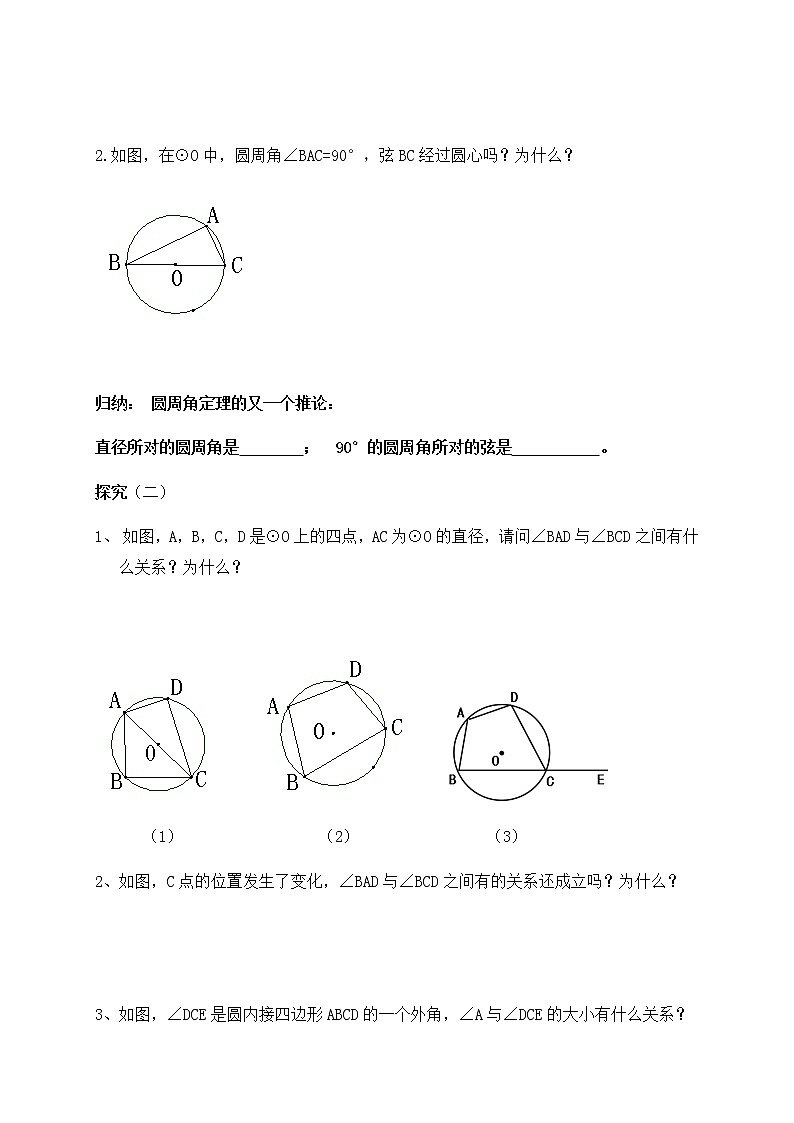
2.如图，在⊙O中，圆周角∠BAC=90°，弦BC经过圆心吗？为什么？

归纳： 圆周角定理的又一个推论：

直径所对的圆周角是        ；  90°的圆周角所对的弦是           。

探究（二）

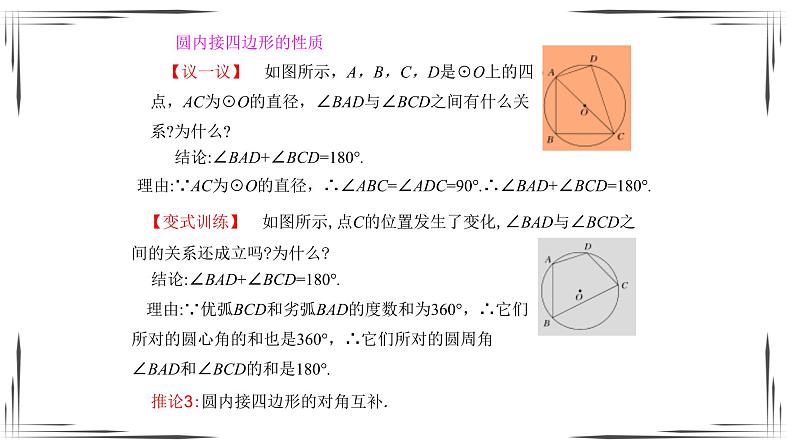
1、如图，A，B，C，D是⊙O上的四点，AC为⊙O的直径，请问∠BAD与∠BCD之间有什么关系？为什么？

      （1）                 （2）                （3）

2、如图，C点的位置发生了变化，∠BAD与∠BCD之间有的关系还成立吗？为什么？

3、如图，∠DCE是圆内接四边形ABCD的一个外角，∠A与∠DCE的大小有什么关系？

归纳：圆内接四边形概念与性质

定义：四边形ABCD的的四个顶点都在⊙O上，这样的四边形叫做圆内接四边形；

这个圆叫做四边形的外接圆.

性质：（1）圆内接四边形的对角_______

     （2）圆内接四边形的外角等于相邻内角的_______

四、随堂练习

1.如图，在⊙O中，△ABC是等边三角形，AD是直径，则∠ADB=    °,∠DAB=     °.

（1）                    （2）

2. 如图，AB是⊙O的直径，若AB=AC，求证：BD=CD.

3.下列关于圆内接四边形叙述正确的有(     )     

①圆内接四边形的任何一个外角都等于它的内对角；②圆内接四边形对角相等；

③圆内接四边形中不相邻的两个内角互补；④在圆内部的四边形叫圆内接四边形.

A.1个      B.2个        C.3个        D.4个

4.如图，AB是⊙O的直径，弦CD与AB相交于点E，∠ACD=60°，∠ADC=50°,

求∠CEB的度数.

5.如图，AB是⊙O的直径，CD是⊙O的弦，AB=6, ∠DCB=30°，求弦BD的长。

五．本课小结：

1.直径所对的圆周角是直角；90°的圆周角所对的弦是直径.

2、圆内接四边形的对角互补.

3、圆内接四边形的外角等于相邻内角的对角

你还有什么收获或困惑？

六.当堂检测：

1.如图，AB是⊙O的直径，∠A=10°,则∠ABC=________.

2.如图，AB是⊙O的直径，CD是弦，∠ACD=40°,则∠BCD=__  _,∠BOD=_   .

（1）                   （2）            （3）          （4）

3.如图，点A、B、C、D在圆上，AB=8,BC=6,AC=10,CD=4.求AD的长.

4.如图，锐角三角形ABC中，∠A=60°，BC为圆O的直径，⊙O交AB、AC于D、E，求证:BC=2DE 

答案：

二．温故知新

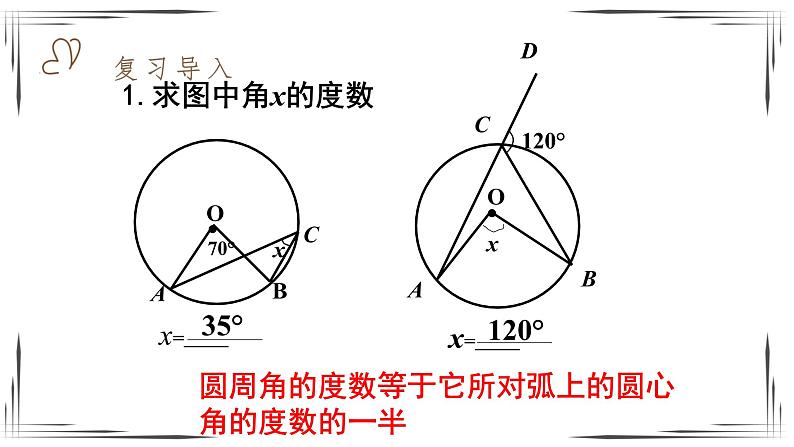
  1．80°，一条弧所对的圆周角等于它所对的圆心角的一半

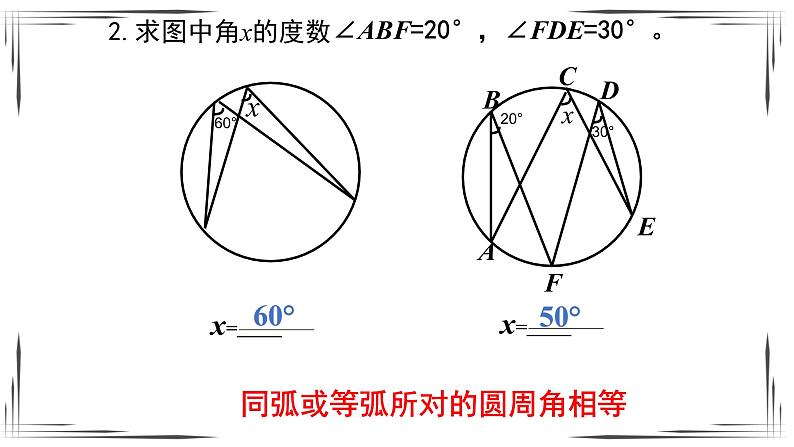
40°，在同圆或等圆中，同弧或等弧所对的圆周角相等

2．90°

五．随堂练习

1. 60 ， 30

2.证明：连接AD，

∵AB是直径，∴∠ADB=90°，即AD垂直BC

∵AB=AC,  ∴CD=DB

3.C

4. 解： 连接BC

∵AB是⊙O的直径， ∴∠ACB=90°

∵∠ABC=∠ADC=50°

∴∠CAB=40°

∴∠CEB=∠CAB+∠ACD=40°+60°=100°

5.解：∵AB是⊙O的直径，∴∠ADB=90°

∵∠DAB=∠DCB=30°，AB=6

∴DB=AB=3

六.当堂检测：

1. 80°    2. 50°，100°.

3.解：∵AB=8,BC=6,AC=10

∴∠ABC=90°

∴AC是⊙O的直径

∴∠ADC=90°

∵AC=10,CD=4

∴AD==2

4. 证明：连接OD，OE，CD

∵BC是⊙O的直径

∴∠BDC=90°=∠ADC

∵∠A=60°

∴∠ACD=30°

则∠DOE=2∠ACD=60°

∵OD=OE

∴△ODE是等边三角形

∴DE=OD=⊙O的半径

∴BC=2DE