初中数学北师大版九年级下册3 垂径定理教学演示ppt课件

这是一份初中数学北师大版九年级下册3 垂径定理教学演示ppt课件，文件包含33垂径定理-课件ppt、33垂径定理-导学案doc、33垂径定理-练习docx、33垂径定理-教案doc等4份课件配套教学资源，其中PPT共17页， 欢迎下载使用。

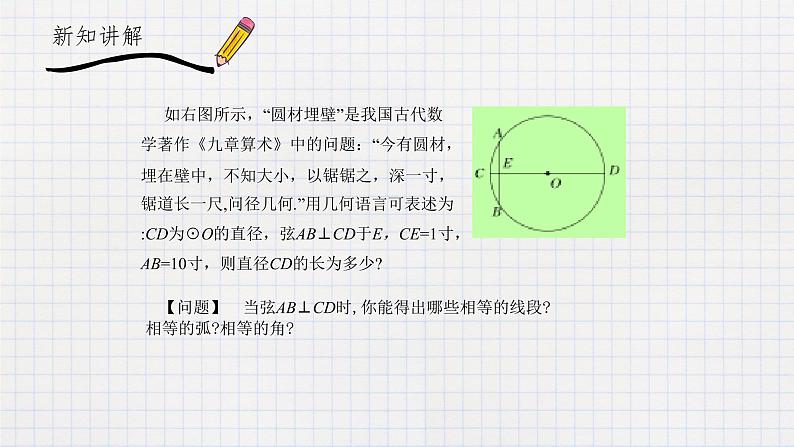
如右图所示，“圆材埋壁”是我国古代数学著作《九章算术》中的问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺,问径几何.”用几何语言可表述为:CD为☉O的直径，弦AB⊥CD于E，CE=1寸，AB=10寸，则直径CD的长为多少?
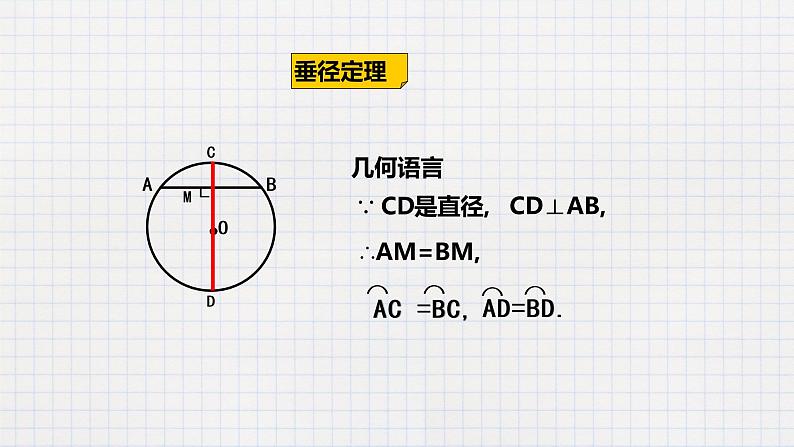
【问题】　当弦AB⊥CD时,你能得出哪些相等的线段?相等的弧?相等的角?
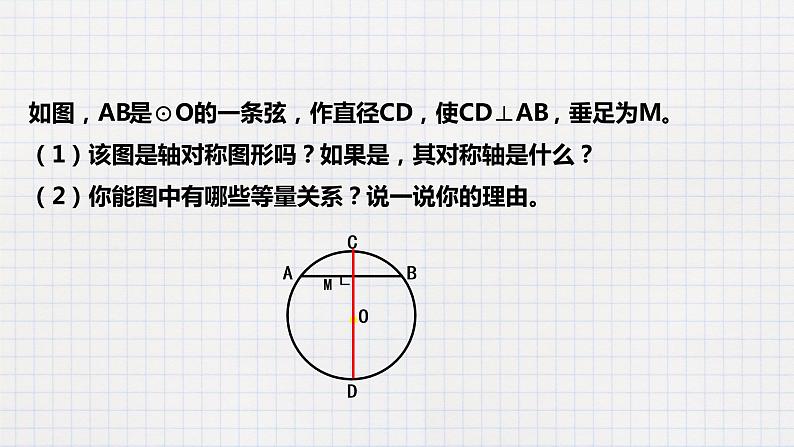
如图，AB是⊙O的一条弦，作直径CD，使CD⊥AB，垂足为M。 （1）该图是轴对称图形吗？如果是，其对称轴是什么？ （2）你能图中有哪些等量关系？说一说你的理由。
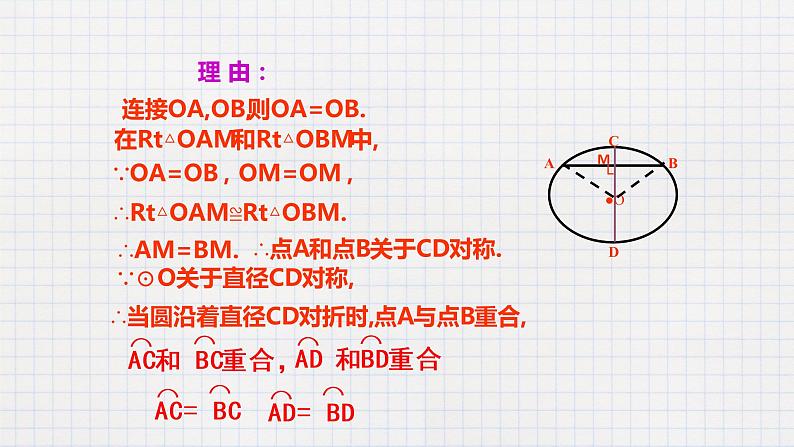
连接OA,OB,则OA=OB.
在Rt△OAM和Rt△OBM中,
∵OA=OB，OM=OM，
∴Rt△OAM≌Rt△OBM.
∴点A和点B关于CD对称.
∵⊙O关于直径CD对称,
∴当圆沿着直径CD对折时,点A与点B重合,
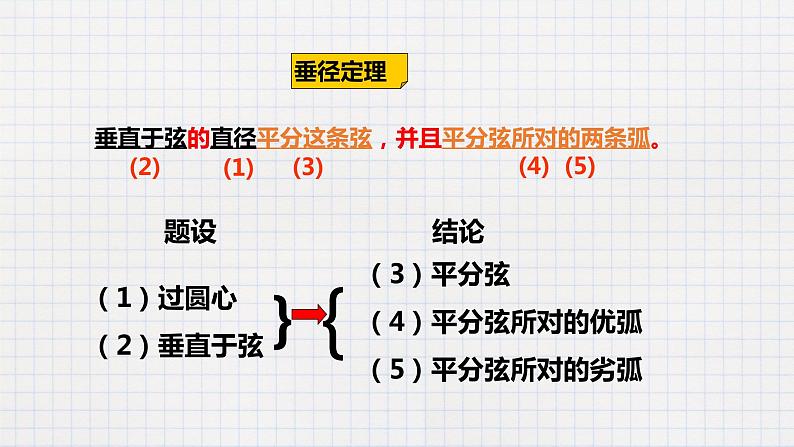
垂直于弦的直径平分这条弦，并且平分弦所对的两条弧。
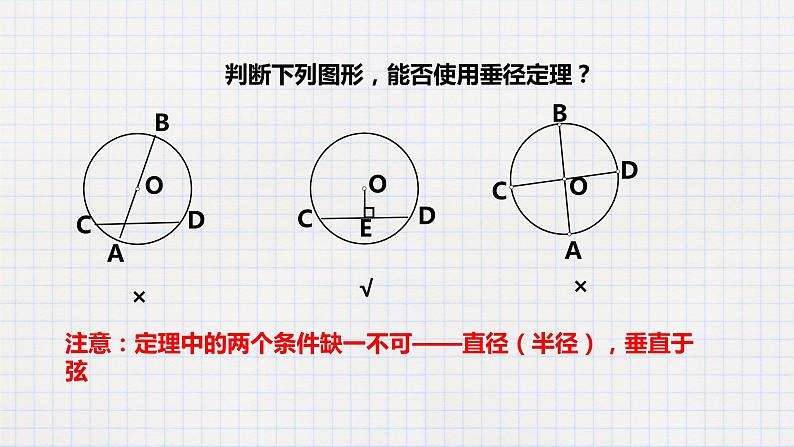
判断下列图形，能否使用垂径定理？
注意：定理中的两个条件缺一不可——直径（半径），垂直于弦
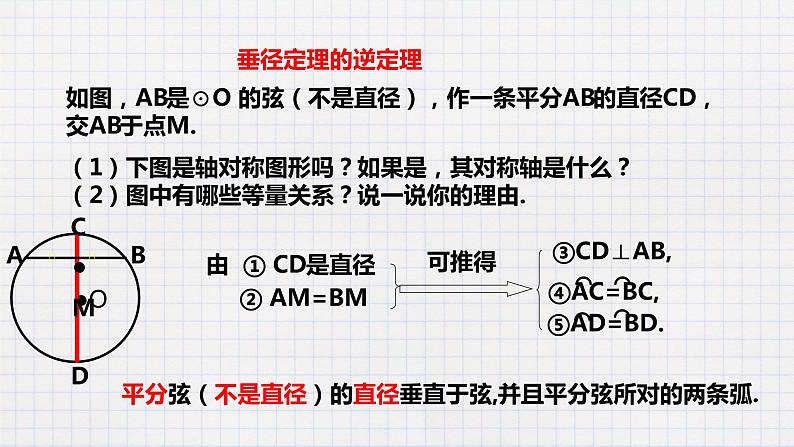
由 ① CD是直径
平分弦（不是直径）的直径垂直于弦,并且平分弦所对的两条弧.
如图，AB是⊙O 的弦（不是直径），作一条平分AB的直径CD，交AB于点M.（1）下图是轴对称图形吗？如果是，其对称轴是什么？ （2）图中有哪些等量关系？说一说你的理由.
平分弦（不是直径）的直径垂直于弦,并且平分弦所对的两条弧. 如果该定理少了“不是直径”，是否也能成立？
垂径定理的逆定理：平分弦（不是直径）的直径垂直于弦,并且平分弦所对的两条弧.
“知二推三” (1)垂直于弦 (2)过圆心 (3)平分弦 (4)平分弦所对的优弧 (5)平分弦所对的劣弧
注意:当具备了(1)(3)时,应对另一 条弦增加”不是直径”的限制.
温馨提示：垂径定理是圆中一个重要的定理,几种条件要相互转化,形成整体,才能运用自如.
垂 径 定 理 的 几 个 基 本 图 形
解这个方程，得R=545.
解：连接OC，设弯路的半径为Rm,则OF=(R-90)m。
根据勾股定理，得 OC²=CF² +OF²
即 R²=300²+(R-90)².
所以，这段弯路的半径为545m.
1.如图所示，☉O的半径为5，弦AB的长为8，点M在线段AB(包括端点A,B)上移动，则OM的取值范围是(　　)A.3≤OM≤5 B.3≤OM＜5C.4≤OM≤5 D.4≤OM＜5
解析:当M与A或B重合时，OM达到最大值，即圆的半径5；当OM⊥AB时，OM取最小值，为 =3.故OM的取值范围是3≤OM≤5.故选A.
2.如图所示，在☉O中，OC⊥弦AB于点C，AB=4，OC=1，则OB的长是　　　　. 
解析:∵OC⊥弦AB于点C，∴BC=AC= AB= ×4=2，在Rt△OBC中，OC=1，BC=2，∴OB= .故填 .
3.如图所示，AB是☉O的直径，弦CD⊥AB，垂足为P.若CD=8，OP=3，则☉O的半径为　　　　. 
解析:连接OC，∵CD⊥AB，CD=8，∴PC= ·CD= ×8=4， 在Rt△OCP中，∵PC=4,OP=3，∴OC= 故填5.
4.如图(1)所示，水平放置的一个油管的截面半径为13 cm，其中有油部分油面宽AB为24 cm，求截面上有油部分油面高CD.
解析:根据垂径定理,易知AC,BC的长,连接OA,根据勾股定理即可求出OC的长,进而可求出CD的值.
解:如图(2)所示，连接OA.根据垂径定理,得AC=BC=12 cm.
在Rt△OAC中，OA=13 cm，AC=12 cm.
根据勾股定理，得OC= =5 cm，∴CD=OD-OC=8 cm.∴油面高CD为8 cm.
通过本节课你学到了什么？