2021-2022学年九年级数学下册基础知识专项讲练（人教版）《反比例函数》全章复习与巩固（知识讲解）学案

这是一份2021-2022学年九年级数学下册基础知识专项讲练（人教版）《反比例函数》全章复习与巩固（知识讲解）学案，共31页。
《反比例函数》全章复习与巩固（知识讲解）
【学习目标】
1．使学生理解并掌握反比例函数的概念，能根据实际问题中的条件确定反比例函数的解析式，能判断一个给定函数是否为反比例函数；
2．能描点画出反比例函数的图象，会用待定系数法求反比例函数的解析式；
3．能根据图象数形结合地分析并掌握反比例函数的性质，能利用这些性质分析和解决一些简单的实际问题.
【要点梳理】
要点一、反比例函数的概念
一般地，形如 (为常数，)的函数称为反比例函数，其中是自变量，是函数，自变量的取值范围是不等于0的一切实数.
特别说明：在中，自变量的取值范围是， ()可以写成()的形式，也可以写成的形式.
要点二、反比例函数解析式的确定
反比例函数解析式的确定方法是待定系数法.由于反比例函数中，只有一个待定系数，因此只需要知道一对的对应值或图象上的一个点的坐标，即可求出的值，从而确定其解析式.
要点三、反比例函数的图象和性质
1.反比例函数的图象
反比例函数的图象是双曲线，它有两个分支，这两个分支分别位于第一、三象限或第二、四象限．它们关于原点对称，反比例函数的图象与轴、轴都没有交点，即双曲线的两个分支无限接近坐标轴，但永远不与坐标轴相交．
特别说明：
观察反比例函数的图象可得：和的值都不能为0，并且图象既是轴对称图形，又是中心对称图形，它有两条对称轴，对称中心是坐标原点．
①的图象是轴对称图形，对称轴为两条直线；
②的图象是中心对称图形，对称中心为原点（0，0）；
③(k≠0)在同一坐标系中的图象关于轴对称，也关于轴对称.

注：正比例函数与反比例函数，
当时，两图象没有交点；当时，两图象必有两个交点，且这两个交点关于原点成中心对称.

2.反比例函数的性质
（1）图象位置与反比例函数性质
　　当时，同号，图象在第一、三象限，且在每个象限内，随的增大而减小；当时，异号，图象在第二、四象限，且在每个象限内，随的增大而增大.
（2）若点()在反比例函数的图象上，则点（）也在此图象上，故反比例函数的图象关于原点对称.
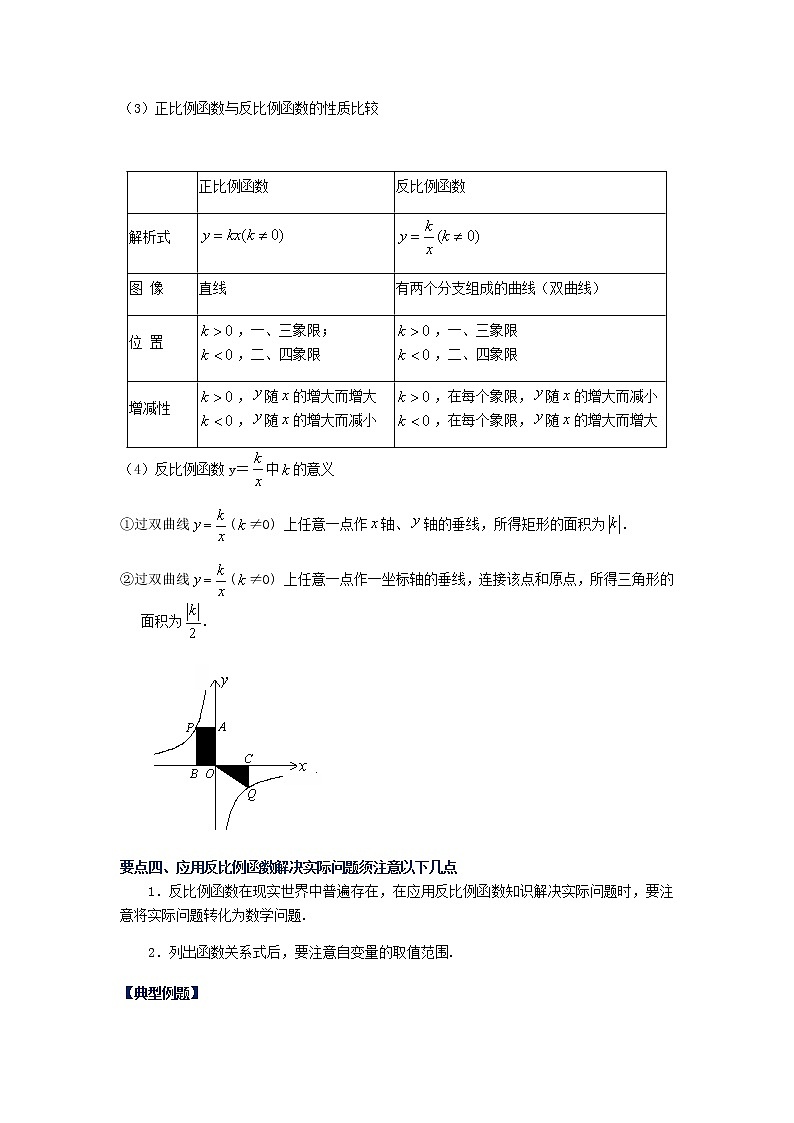
（3）正比例函数与反比例函数的性质比较

　
正比例函数
反比例函数
解析式


图 像
直线
有两个分支组成的曲线（双曲线）
位 置
，一、三象限；
，二、四象限
，一、三象限
，二、四象限
增减性
，随的增大而增大
，随的增大而减小
，在每个象限，随的增大而减小
，在每个象限，随的增大而增大
（4）反比例函数y＝中的意义
①过双曲线(≠0) 上任意一点作轴、轴的垂线，所得矩形的面积为.
②过双曲线(≠0) 上任意一点作一坐标轴的垂线，连接该点和原点，所得三角形的面积为.

要点四、应用反比例函数解决实际问题须注意以下几点
　　1．反比例函数在现实世界中普遍存在，在应用反比例函数知识解决实际问题时，要注意将实际问题转化为数学问题.
2．列出函数关系式后，要注意自变量的取值范围.
【典型例题】
类型一、确定反比例函数的解析式
1． 已知反比例函数y＝（k≠0），当x＝﹣3时，y＝．
（1）求y关于x的函数表达式．
（2）当y＝﹣4时，求自变量x的值．
【答案】（1）y＝﹣；（2）x＝1
【分析】
（1）将x＝﹣3，y＝代入y＝（k≠0），即利用待定系数法求该函数的解析式；
（2）将y＝﹣4代入（1）中的反比例函数解析式，求x值即可．
解：（1）根据题意，得
＝﹣，
解得，k＝﹣4；
∴该反比例函数的解析式是y＝﹣；
（2）由（1）知，该反比例函数的解析式是y＝﹣，
∴当y＝﹣4时，﹣4＝﹣，即x＝1．
【点拨】本题考查了待定系数法求反比例函数的解析式．在解答该题时，还利用了反比例函数图象上点的坐标特征，求函数值对应得自变量的值．
举一反三：
【变式1】如图，在平面直角坐标系中，一次函数的图象与轴、轴分别交于两点，与反比例函数的图象交于两点．
（1）求该反比例函数的解析式；
（2）求的面积；
（3）请根据图象直接写岀不等式的解集．

【答案】（1）；（2）8；（3）或
【分析】
（1）把两点代入一次函数解析式中，求得的值，再用待定系数法求反比例函数的解析式即可；
（2）根据和点的坐标求解即可；
（3）根据函数图象写出直线在双曲线上方部分的x的取值范围即可
解：（1）把，代入得，，，

，
反比例函数的关系式为，
（2）令 则

，
答：的面积为；
（3）
所以，不等式的解集是或
【点拨】本题考查了一次函数的性质，待定系数法求解析式，反比例函数与一次函数的交点问题及不等式，数形结合是解决此题的关键．
【变式2】反比例函数y=（k为常数，且k≠0）的图象经过点A（1，3）、B（3，m）．
（1）求反比例函数的解析式及B点的坐标；
（2）在x轴上找一点P，使PA+PB的值最小，求满足条件的点P的坐标．

【答案】(1); B点坐标为（3，1）；(2) P点坐标为（，0）．
【分析】（1）先把A点坐标代入y=求出k得到反比例函数解析式；然后把B（3，m）代入反比例函数解析式求出m得到B点坐标；
（2）作A点关于x轴的对称点A′，连接BA′交x轴于P点，则A′（1，﹣3），利用两点之间线段最短可判断此时此时PA+PB的值最小，再利用待定系数法求出直线BA′的解析式，然后求出直线与x轴的交点坐标即可得到P点坐标．
解：（1）把A（1，3）代入y=得k=1×3=3，
∴反比例函数解析式为y=；
把B（3，m）代入y=得3m=3，解得m=1，
∴B点坐标为（3，1）；
（2）作A点关于x轴的对称点A′，连接BA′交x轴于P点，则A′（1，﹣3），
∵PA+PB=PA′+PB=BA′，
∴此时PA+PB的值最小，
设直线BA′的解析式为y=mx+n，
把A′（1，﹣3），B（3，1）代入得，解得，
∴直线BA′的解析式为y=2x﹣5，
当y=0时，2x﹣5=0，解得x=，
∴P点坐标为（，0）．

【点睛】本题考查了用待定系数法求反比例函数的解析式、最短路径问题，熟练掌握待定系数法求函数解析式是解题的关键.
类型二、反比例函数的图象及性质
2． 已知反比例函数y＝(k≠0)的图象经过点B(3，2)，点B与点C关于原点O对称，BA⊥x轴于点A，CD⊥x轴于点D
（1）求这个反比函数的表达式；
（2）求△ACD的面积．

【答案】（1 ）；（2）6.
【详解】
试题分析：（1）将B点坐标代入y＝中，求得k值，即可得反比例函数的解析式；（2）分别求得点C、点A、点D的坐标，即可求得△ACD的面积．
解 ：(1)将B点坐标代入y＝中，得＝2，解得k＝6，
∴反比例函数的解析式为y＝.
(2)∵点B与点C关于原点O对称，
∴C点坐标为(－3，－2)．
∵BA⊥x轴，CD⊥x轴，
∴A点坐标为(3，0)，D点坐标为(－3，0)．
∴S△ACD＝AD·CD＝×[3－(－3)]×|－2|＝6
举一反三：
【变式1】如图，在平面直角坐标系中，过点M（0，2）的直线l与x轴平行，且直线l分别与反比例函数y=（x＞0）和y=（x＜0）的图象交于点P、点Q．
（1）求点P的坐标；
（2）若△POQ的面积为8，求k的值．

【答案】（1）点坐标为；（2）.
【分析】
（1）求出P点的纵坐标，再代入函数解析式，即可求出答案；
（2）根据三角形的面积公式求出PQ，求出MQ，求出点Q的坐标，即可求出答案．
解：∵轴，
∴点的纵坐标为，
把代入得，
∴点坐标为；
∵，
∴，
∴，
而，
∴．
【点拨】本题考查了用待定系数法求反比例函数的解析式和反比例函数图象上点的坐标特征等知识点，能灵活运用知识点进行计算是解此题的关键．
【变式2】如图，已知反比例函数y= （k≠0）的图象经过点A（﹣2，m），过点A作AB⊥x轴于点B，且△AOB的面积为4．

（1）求k和m的值；
（2）设C（x，y）是该反比例函数图象上一点，当1≤x≤4时，求函数值y的取值范围．
【答案】（1）k=﹣8，m=4；（2）﹣8≤y≤﹣2
【分析】
（1）根据三角形的面积公式先得到m的值，然后把点A的坐标代入y=，可求出k的值；
（2）先分别求出x=1和4时，y的值，再根据反比例函数的性质求解．
解 ：（1）∵△AOB的面积为4，
∴(−xA)•yA＝4，
即可得：k=xA•yA=﹣8，
令x=2，得：m=4；
（2）当1≤x≤4时，y随x的增大而增大，
令x=1，得：y=﹣8；
令x=4，得：y=﹣2，
所以﹣8≤y≤﹣2即为所求．
【点拨】本题考查了反比例函数图象上点的坐标特征，点在图象上，点的横纵坐标满足图象的解析式；也考查了反比例函数的性质，三角形的面积公式以及代数式的变形能力．
3． 如图，双曲线y＝上的一点A（m，n），其中n＞m＞0，过点A作AB⊥x轴于点B，连接OA．
（1）已知△AOB的面积是3，求k的值；
（2）将△AOB绕点A逆时针旋转90°得到△ACD，且点O的对应点C恰好落在该双曲线上，求的值．

【答案】（1）6；（2）
【分析】
（1）依据△AOB的面积是3，即可得到mn=6，进而得出k的值；
（2）延长DC交x轴于E，依据四边形ABED是矩形，即可得到DE=AB=n，CE=n-m，OE=m+n，进而得到C（m+n，n-m），根据点A，C都在双曲线上，即可得到mn=（m+n）（n-m），进而得出的值．
解：（1）∵双曲线y＝上的一点A（m，n），过点A作AB⊥x轴于点B，
∴AB＝n，OB＝m，
又∵△AOB的面积是3，
∴mn＝3，
∴mn＝6，
∵点A在双曲线y＝上，
∴k＝mn＝6；
（2）如图，延长DC交x轴于E，
由旋转可得△AOB≌△ACD，∠BAD＝90°，
∴AD＝AB＝n，CD＝OB＝m，∠ADC＝90°，
∵AB⊥x轴，
∴∠ABE＝90°，
∴四边形ABED是矩形，
∴∠DEB＝90°，
∴DE＝AB＝n，CE＝n﹣m，OE＝m+n，
∴C（m+n，n﹣m），
∵点A，C都在双曲线上，
∴mn＝（m+n）（n﹣m），
即m2+mn﹣n2＝0，
方程两边同时除以n2，得
+﹣1＝0，
解得＝，
∵n＞m＞0，
∴＝．

【点拨】本题考查了反比例函数系数k的几何意义，解题时注意：在反比例函数的图象上任意一点向坐标轴作垂线，这一点和垂足以及坐标原点所构成的三角形的面积是|k|，且保持不变．
举一反三：
【变式1】如图，正比例函数的图像与反比例函数的图像交于点．点B为x轴正半轴上一点，过B作x轴的垂线交反比例函数的图像于点C，交正比例函数的图像于点D．

（1）求a的值及正比例函数的表达式；
（2）若，求的面积．
【答案】（1）a=2；y=2x；（2）
【分析】
（1）已知反比例函数解析式，点A在反比例函数图象上，故a可求；求出点A的坐标后，点A同时在正比例函数图象上，将点A坐标代入正比例函数解析式中，故正比例函数的解析式可求．
（2）根据题意以及第一问的求解结果，我们可设B点坐标为(b，0)，则D点坐标为(b，2b)，根据BD=10，可求b值，然后确认三角形的底和高，最后根据三角形面积公式即可求解．
解 ：（1）已知反比例函数解析式为y=，点A(a，4)在反比例函数图象上,将点A坐标代入，解得a=2，故A点坐标为(2，4)，又∵A点也在正比例函数图象上，设正比例函数解析为y=kx，将点A(2，4)代入正比例函数解析式中，解得k=2，则正比例函数解析式为y=2x．
故a=2；y=2x．
（2）根据第一问的求解结果，以及BD垂直x轴，我们可以设B点坐标为(b，0)，则C点坐标为(b，)、D点坐标为(b，2b)，根据BD=10，则2b=10，解得b=5，故点B的坐标为(5，0)，D点坐标为(5，10)，C点坐标为(5，)，则在△ACD中，=．
故△ACD的面积为．
【点拨】（1）本题主要考查求解正比例函数及反比例函数解析式，掌握求解正比例函数和反比例函数解析式的方法是解答本题的关键．
（2）本题根据第一问求解的结果以及BD垂直x轴，利用待定系数法，设B、C、D三点坐标，求出B、C、D三点坐标，是解答本题的关键，同时掌握三角形面积公式，即可求解．
类型三、反比例函数与一次函数综合
4． 如图，一次函数y=﹣x+4的图象与反比例函数y=（k为常数，且k≠0）的图象交于A（1，a），B（3，b）两点．
（1）求反比例函数的表达式
（2）在x轴上找一点P，使PA+PB的值最小，求满足条件的点P的坐标
（3）求△PAB的面积．

【答案】（1）反比例函数的表达式y=，（2）点P坐标（，0）， (3)S△PAB= 1.5．
【解析】
（1）把点A（1，a）代入一次函数中可得到A点坐标，再把A点坐标代入反比例解析式中即可得到反比例函数的表达式；（2）作点D关于x轴的对称点D，连接AD交x轴于点P，此时PA+PB的值最小.由B可知D点坐标，再由待定系数法求出直线AD的解析式，即可得到点P的坐标；（3）由S△PAB=S△ABD﹣S△PBD即可求出△PAB的面积.
解：（1）把点A（1，a）代入一次函数y=﹣x+4，
得a=﹣1+4， 
解得a=3， 
∴A（1，3）， 
点A（1，3）代入反比例函数y=， 
得k=3，  
∴反比例函数的表达式y=， 
（2）把B（3，b）代入y=得，b=1
∴点B坐标（3，1）；
作点B作关于x轴的对称点D，交x轴于点C，连接AD，交x轴于点P，此时PA+PB的值最小， 
∴D（3，﹣1），
设直线AD的解析式为y=mx+n， 
把A，D两点代入得，， 解得m=﹣2，n=5， 
∴直线AD的解析式为y=﹣2x+5，
令y=0，得x=， 
∴点P坐标（，0），

(3)S△PAB=S△ABD﹣S△PBD=×2×2﹣×2×=2﹣=1.5．
点晴：本题是一道一次函数与反比例函数的综合题，并与几何图形结合在一起来求有关于最值方面的问题.此类问题的重点是在于通过待定系数法求出函数图象的解析式，再通过函数解析式反过来求坐标，为接下来求面积做好铺垫.
举一反三：
【变式1】如图，反比例函数和一次函数的图象都经过点和点．

（1）_________，_________；
（2）求一次函数的解析式，并直接写出时x的取值范围；
（3）若点P是反比例函数的图象上一点，过点P作轴，垂足为M，则的面积为_________．
【答案】（1）4，2；（2）y=-2x+6，1＜x＜2；（3）2
【分析】
（1）把A(1,4)代入求出m的值；再将y=2代入反比例函数式，即可求出n的值；
（2）由（1）可知A、B两点的坐标，将这两点的坐标代入求出k、b的值即可，再根据t图象判定出时x的取值范围；
（3）设P点横坐标为a,则纵坐标为，即可知道OM、PM，进而求出面积即可．
解：（1）把x=1,y=4代入得，
4=，
解得m=4
∴
当y=2时，2=
解得，n=2
（2）把A(1,4)，B(2,2)分别代入得
解得
∴y2=-2x+6
当y1＜y2时，从图象看得出：1 100
∴蔬菜运输汽车早上8:00从巴东出发，不能在中午1:00到达武汉市场；
（3）∵7≤t≤9.5，
∴≤u≤，即≤u≤．
答：平均速度的取值范围是≤u≤．
【点拨】本题考查反比例函数的应用、待定系数法等知识点，理解题意、求得函数解析式是解答本题的关键．
【变式3】已知某品牌运动鞋每双进价120元，为求合适的销售价格进行了4天的试销，试销情况如下表：

第1天
第2天
第3天
第4天
售价x（元/双）
150
200
250
300
销售量y（双）
40
30
24
20
（1）表中数据x、y满足什么函数关系式？请求出这个函数关系式；
（2）若每天销售利润为3000元，则单价应定为多少元？
【答案】（1）y＝；（2）若商场计划每天的销售利润为3000元，则其单价应定为240元．
【分析】
（1）根据表中的数据可以判断x与y的函数关系，本题即可解决；
（2）根据题意列出方程进行求解即可得到答案.
解：（1）由表中数据得：xy＝6000，
∴y＝，
∴y是x的反比例函数，
y与x之间的函数关系式为y＝；
（2）由题意得，（x﹣120）•＝3000，
∴
解得，x＝240；
经检验，x＝240是原方程的根，
∴单价应定为240元.
答：若商场计划每天的销售利润为3000元，则其单价应定为240元．
【点拨】本题主要考查了反比例函数的应用，解题的关键在于能够准确找到等量关系列出方程求解.