全国通用中考数学第二轮总复习课件专题1.6 最值问题-隐圆模型之瓜豆问题

这是一份全国通用中考数学第二轮总复习课件专题1.6 最值问题-隐圆模型之瓜豆问题，共32页。PPT课件主要包含了隐圆模型，定点定长型，直角对直径，定边对定角，定角夹定高，四点共圆型，“米勒”问题，“瓜豆”问题，轨迹之圆篇，轨迹之线段篇等内容，欢迎下载使用。

在辅助圆问题中,我们了解了求关于动点最值问题的方式之一——求出动点轨迹,即可求出关于动点的最值. 本文继续讨论另一类动点引发的最值问题,在此类题目中，题目或许先描述的是动点P,但最终问题问的可以是另一点Q,当然P、Q之间存在某种联系,从P点出发探讨Q点运动轨迹并求出最值,为常规思路.
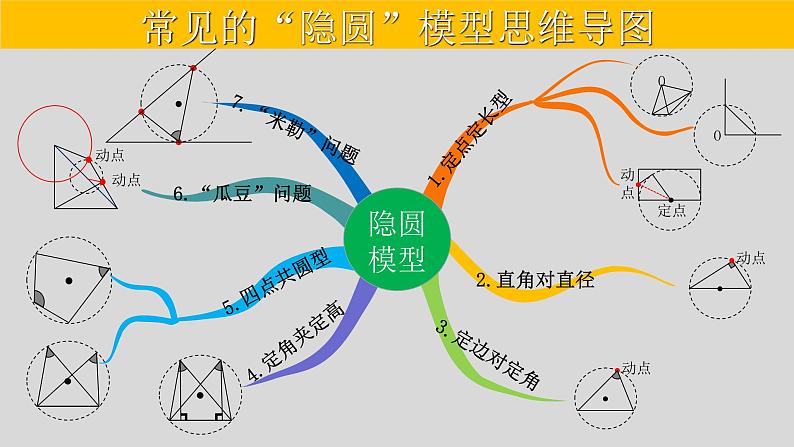
常见的“隐圆”模型思维导图
模型解读---轨迹之圆篇
【引例1】如图,P是圆O上一个动点,A为定点,连接AP,Q为AP中点.【思考】当点P在圆O上运动时,Q点轨迹是？
【分析】观察动图可知点Q轨迹是个圆,而我们还需确定的是此圆与圆O有什么关系?考虑到Q点始终为AP中点,连接AO,取AO中点M,连接QM,PO,任意时刻,QM:PO=AQ:AP=1:2.则M点即为Q点轨迹圆圆心,半径MQ是OP一半,
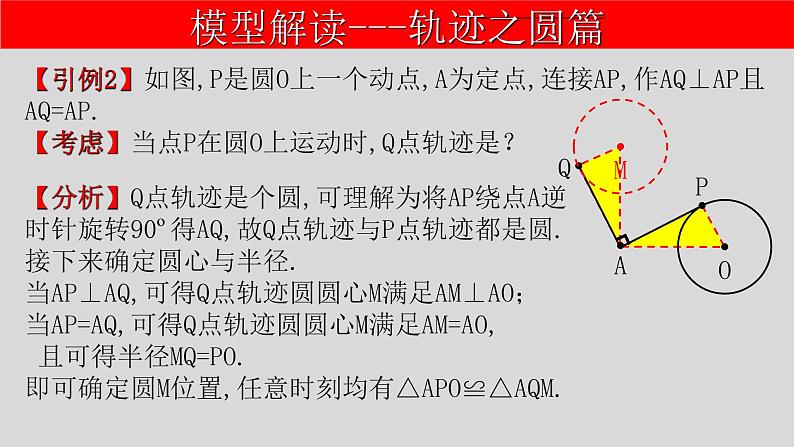
【引例2】如图,P是圆O上一个动点,A为定点,连接AP,作AQ⊥AP且AQ=AP.【考虑】当点P在圆O上运动时,Q点轨迹是？
【分析】Q点轨迹是个圆,可理解为将AP绕点A逆时针旋转90º得AQ,故Q点轨迹与P点轨迹都是圆.接下来确定圆心与半径.当AP⊥AQ,可得Q点轨迹圆圆心M满足AM⊥AO；当AP=AQ,可得Q点轨迹圆圆心M满足AM=AO, 且可得半径MQ=PO.即可确定圆M位置,任意时刻均有△APO≌△AQM.
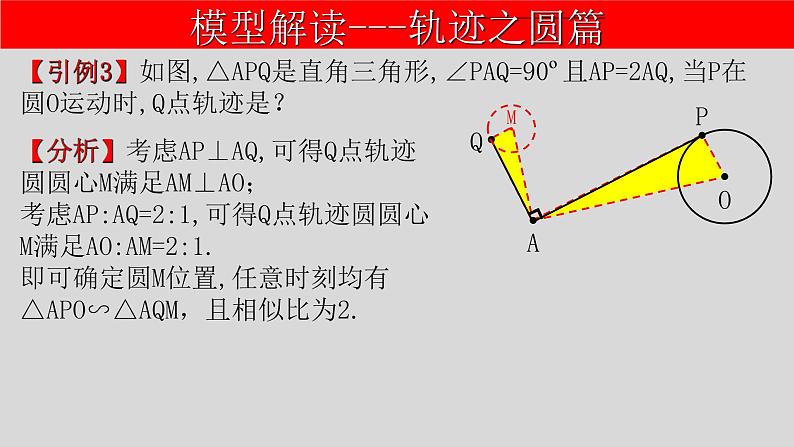
【引例3】如图,△APQ是直角三角形,∠PAQ=90º且AP=2AQ,当P在圆O运动时,Q点轨迹是？
【分析】考虑AP⊥AQ,可得Q点轨迹圆圆心M满足AM⊥AO；考虑AP:AQ=2:1,可得Q点轨迹圆圆心M满足AO:AM=2:1.即可确定圆M位置,任意时刻均有△APO∽△AQM，且相似比为2.
模型总结---轨迹之圆篇
【总结】为了便于区分动点P、Q,可称点P为“主动点”,点Q为“从动点”.此类问题的必要条件：两个定量主动点、从动点与定点连线的夹角是定量(∠PAQ是定值)；主动点、从动点到定点的距离之比是定量(AP:AQ是定值)．
【结论】(1)主、从动点与定点连线的夹角等于两圆心与定点连线的夹角：∠PAQ=∠OAM；(2)主、从动点与定点的距离之比等于两圆心到定点的距离之比：AP:AQ=AO:AM,也等于两圆半径之比.按以上两点即可确定从动点轨迹圆,Q与P的关系相当于旋转+伸缩.古人云：种瓜得瓜,种豆得豆.“种”圆得圆,“种”线得线，谓之“瓜豆原理”.
【思考1】如图,P是圆O上一个动点,A为定点,连接AP,以AP为一边作等边△APQ.【考虑】当点P在圆O上运动时,Q点轨迹是?
【分析】Q点满足(1)∠PAQ=60º；(2)AP=AQ，故Q点轨迹是个圆：1)当∠PAQ=60º,可得Q点轨迹圆圆心M满足∠MAO=60º；2)当AP=AQ,可得Q点轨迹圆圆心M满足AM=AO,且可得半径MQ=PO.即可确定圆M位置,任意时刻均有△APO≌△AQM．
【小结】可以理解AQ由AP旋转得来,故圆M亦由圆O旋转得来,旋转角度与缩放比例均等于AP与AQ的位置和数量关系.
【思考2】如图,P是圆O上一个动点,A为定点,连接AP,以AP为斜边作等腰直角△APQ.【考虑】当点P在圆O上运动时,如何作出Q点轨迹？
【例1】如图,已知P是⊙O外一点,Q是⊙O上的动点,线段PQ的中点为M,连接OP,OM.若⊙O的半径为2,OP=4,则线段OM的最小值是(　) A.0 B.1 C.2 D.3
典型例题---轨迹之圆篇
1.如图,点P(3,4),圆P半径为2,A(2.8,0),B(5.6,0),点M是圆P上的动点,点C是MB的中点,则AC的最小值是_______．
当堂训练---轨迹之圆篇
【分析】M点为主动点,C点为从动点,B点为定点.考虑C是BM中点,可知C点轨迹：取BP中点N,以N为圆心,NC为半径作圆,即为点C轨迹.
【分析】当A,C,N三点共线且点C在线段NA上时,AC取到最小值,根据B,P坐标求N,利用两点间距离公式求得NA,再减去NC即可.
2.如图,在等腰Rt△ABC中,AC=BC= ,点P在以斜边AB为直径的半圆上,M为PC的中点,当半圆从点A运动至点B时,点M运动的路径长为____．
【分析】∵C,M,P共线及M是CP中点,可确定M点轨迹：取AB中点O(M),连接CO取CO中点D,以D为圆心,DM为半径作圆D分别交AC,BC于E,F两点,则弧EF即为M点轨迹. 当然,若能理解M点与P点轨迹关系,可直接得到M点的轨迹长为P点轨迹长一半,即可解决问题.
3.如图,正方形ABCD中,AB= ,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90º得DF,连接AE、CF.求线段OF长的最小值.
【分析】E是主动点,F是从动点，D是定点,E点满足EO=2,故E点轨迹是以O为圆心,2为半径的圆. 当DE⊥DF且DE=DF,故作DM⊥DO且DM=DO,F点轨迹是以点M为圆心,2为半径的圆. 连接OM,与圆M交点即为F点,此时OF最小.可构造三垂直全等求线段长,再利用勾股定理求得OM,减去MF即可得到OF的最小值.
4.△ABC中,AB=4,AC=2,以BC为边在△ABC外作正方形BCDE，BD、CE交于点O,则线段AO的最大值为_____．
【分析】AB、AC均为定值,可以固定其中一条,比如固定AB,将AC看成动线段,由此引发正方形BCED的变化,求得线段AO的最大值. 根据AC=2,可得C点轨迹是以点A为圆心,2为半径的圆.接下来题目求AO的最大值,所以确定O点轨迹即可,观察△BOC是等腰直角三角形,锐角顶点C的轨迹是以点A为圆心,2为半径的圆,所以O点轨迹也是圆,以AB为斜边构造等腰直角三角形,直角顶点M即为点O轨迹圆圆心. 连接AM并延长与圆M交点即为所求的点O,此时AO最大,根据AB先求AM,再根据BC与BO的比值可得圆M的半径与圆A半径的比值,得到MO,相加即得AO. 此题方法也不止这一种,比如可以如下构造旋转,当A、C、A´共线时,可得AO最大值.或者直接利用“托勒密定理”可得最大值.
5.如图,在Rt△ABC中,∠ACB=90º,AC=8,BC=6,点D是平面内的一个动点,且AD=4,M为BD的中点.设线段CM长度为a,在D点运动过程中,a的取值范围是_________.
【分析】本题是双动点问题,按照“主动支配从动,从动跟随主动,动中找定”构想,回归到“动中取静”的策略.你能读懂“点D是平面内的一个动点,且AD=4”这句话的含义吗?D是动点但不是随意的点,而是以A为圆心,AD=4的长为半径的作圆周运动。
主从联动型,主动点轨迹为圆则从动点的轨迹也是圆主动点---定点定长型→从动点---定点定长型
构图如图2：通过显示圆作出主动点D、从动点M运动的轨迹.主动点D运动轨迹：以定点A为圆心、AD=4为半径作圆.从动点M运动轨迹:以定点AB的中点P为圆心,0.5AD=2长为半径的作圆.发现：圆生圆,有相似解：在Rt△ABC中：中线PC=0.5AB=5, 在△ABD中：中位线PM=0.5AD=2CM的范围转化为“圆外定点到圆上最值”问题,即C、P、M三点共线问题.运动到如图3位置时： CM最大=PC+PM=5+2=7运动到如图4位置时： CM最小=PC-PM=5-2=3
引例：如图,A为直线BC外一定点,P是直线BC上一动点,连接AP,取AP中点Q,当点P在BC上运动时,Q点轨迹是?
【分析】当P点轨迹是直线时,Q点轨迹也是一条直线. 可以这样理解：分别过A、Q向BC作垂线,垂足分别为M、N,在运动过程中,因为AP=2AQ,所以QN始终为AM的一半,即Q点到BC的距离是定值,故Q点轨迹是一条直线.
模型解读---轨迹之线段篇
【引例】如图,△APQ是等腰直角三角形,∠PAQ=90º且AP=AQ,当点P在直线BC上运动时,求Q点轨迹?
【分析】当AP与AQ夹角固定且AP:AQ为定值的话,P、Q轨迹是同一种图形. 当确定轨迹是线段的时候,可以任取两个时刻的Q点的位置,连线即可,比如Q点的起始位置和终点位置,连接即得Q点轨迹线段.
必要条件:主动点、从动点与定点连线的夹角是定量(∠PAQ是定值)；主动点、从动点到定点的距离之比是定量(AP:AQ是定值).结论：P、Q两点轨迹所在直线的夹角等于∠PAQ(当∠PAQ≤90º时，∠PAQ等于MN与BC夹角)P、Q两点轨迹长度之比等于AP:AQ(由△ABC∽△AMN,可得AP:AQ=BC:MN)
模型总结---轨迹之线段篇
【例2】如图,在等边△ABC中,AB=10,BD=4,BE=2,点P从点E出发沿EA方向运动,连结PD,以PD为边,在PD的右侧按如图所示的方式作等边△DPF,当点P从点E运动到点A时,点F运动的路径长是____.
【分析】根据△DPF是等边三角形,所以可知F点运动路径长与P点相同,P从E点运动到A点路径长为8,故此题答案为8.
典型例题---轨迹之线段篇
1.如图,△ABC是边长为4的等边三角形,AD为BC边上的高线,点E为线段AD上一动点,连接CE,将CE绕点C逆时针旋转60º得到线段CF,连接DF.DF的最小值是____.
一个定点----垂线段最短
当堂训练---轨迹之线段篇
2.如图,已知等边三角形ABC的边长为8,点D为AB边上一动点,DE始终平行于BC,MN为△ADE的中位线,现将点D开始沿AB方向移动,移动到点B处停止,在整个移动过程中线段MN扫过的面积是_____.
3.如图,∠AOB=60º,OA=OB,动点C从点O出发,沿射线OB方向移动,以AC为边在右侧作等边△ACD,连接BD,则BD所在直线与OA所在直线的位置关系是( 　) A.平行 B.相交 C.垂直 D.平行、相交或垂直
所谓“瓜豆原理”,就是主动点的轨迹与从动点的轨迹是相似性,根据主、从动点与定点连线形成的夹角以及主、从动点到定点的距离之比,可确定从动点的轨迹,而当主动点轨迹是其他图形时,从动点轨迹必然也是．
【例3】如图,在反比例函数 的图像上有一动点A,连接AO并延长交图像的另一支于点B,在第一象限内一点C,满足AC=BC,当点A运动时,点C始终在函数 的图像上运动,若tan∠CAB=2,则k的值为( )A.2 B.4 C.6 D.8
【分析】∠AOC=90º且AO:OC=1:2,∴点C的轨迹也是一条双曲线,分别作AM、CN垂直x轴,垂足分别为M、N,连接OC,易证△AMO∽△ONC,∴CN=2OM,ON=2AM,∴ON·CN=4AM·OM,故k=4×2=8. 【思考】若将条件“tan∠CAB=2”改为“△ABC是等边三角形”，k会是多少?
当堂训练---轨迹之线段篇
1.如图,A(-1,1),B(-1,4),C(-5,4),点P是△ABC边上一动点,连接OP,以OP为斜边在OP的右上方作等腰直角△OPQ,当点P在△ABC边上运动一周时,点Q的轨迹形成的封闭图形面积为___.
【分析】根据△OPQ是等腰直角三角形可得：点Q的运动轨迹与点P的轨迹形状相同，根据OP:OQ= ,可得点P的轨迹图形与点Q的轨迹图形相似比为 ，故面积比为2:1,△ABC面积为0.5×3×4=6，故点Q的轨迹形成的封闭图形面积为3.【小结】根据瓜豆原理，类似这种求从动点轨迹长或者轨迹图形面积，根据主动点轨迹推导即可，甚至无需作图.