全国通用中考数学第二轮总复习课件专题1.10 最值问题-函数最值模型

这是一份全国通用中考数学第二轮总复习课件专题1.10 最值问题-函数最值模型，共22页。PPT课件主要包含了一次函数的闭区间最值，二次函数的闭区间最值，长度的最值问题，面积的最值问题，0≤x≤50，x＞50，如图1，如图2，yax2+bx+c等内容，欢迎下载使用。
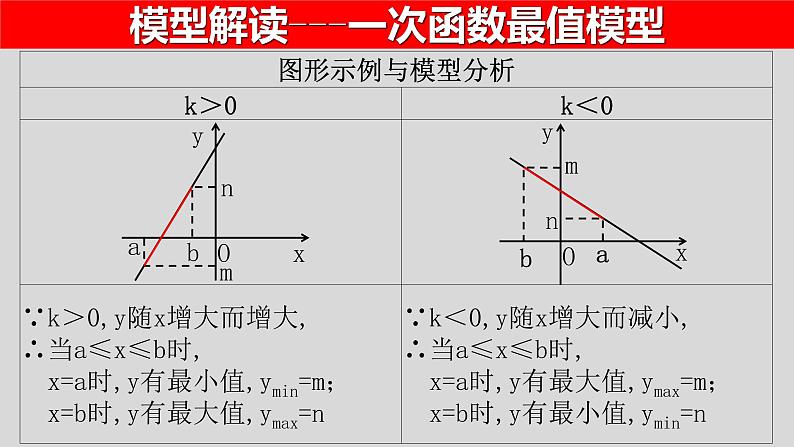
模型解读---一次函数最值模型
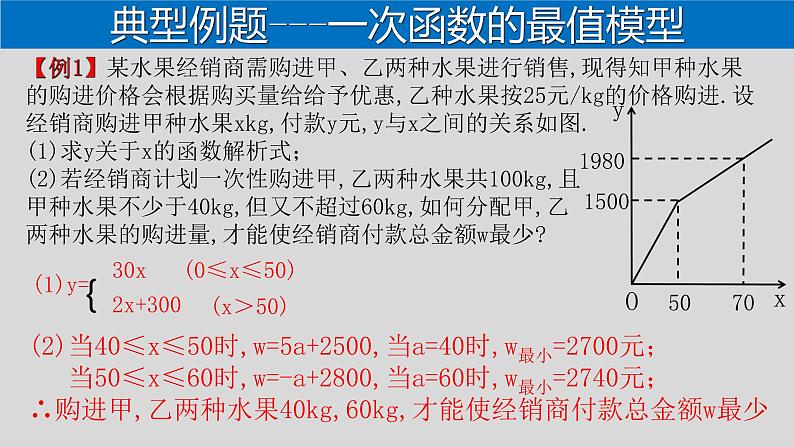
典型例题---一次函数的最值模型
【例1】某水果经销商需购进甲、乙两种水果进行销售,现得知甲种水果的购进价格会根据购买量给给予优惠,乙种水果按25元/kg的价格购进.设经销商购进甲种水果xkg,付款y元,y与x之间的关系如图.(1)求y关于x的函数解析式；(2)若经销商计划一次性购进甲,乙两种水果共100kg,且甲种水果不少于40kg,但又不超过60kg,如何分配甲,乙两种水果的购进量,才能使经销商付款总金额w最少?
(2)当40≤x≤50时,w=5a+2500,当a=40时,w最小=2700元； 当50≤x≤60时,w=-a+2800,当a=60时,w最小=2740元；∴购进甲,乙两种水果40kg,60kg,才能使经销商付款总金额w最少.
(3)若甲、乙两种水果的销售价格分别为40元/千克和36元/千克.经销商按(2)中甲、乙两种水果的购进的分配比例购进两种水果共a千克,且销售完a千克水果获得的利润不少于1650元,求a的最小值.
当堂训练---一次函数最值模型
1.某大学生利用业余时间经营了一家网店,销售一种成本为30元/件的文化衫,根据以往的销售经验,他整理出这种文化衫的售价y1(元/件),销量y2(件)与第x(1≤x＜90)天的函数图象如图所示.(1)求y1,y2与x的函数关系式；(2)求每天的销售利润W与x的函数关系式；(3)销售这种文化衫的第几天时销售利润最大?最大利润是多少?
y2=-2x+200(1≤x＜90)
(3)当1≤x＜50时,w=-2(x-45)2+6050,∴当x=45时,wmax=6050 当50≤x＜90时,w=-120x+12000,∴当x=50时,wmax=6000综上所述：当x=45时,wmax=6050
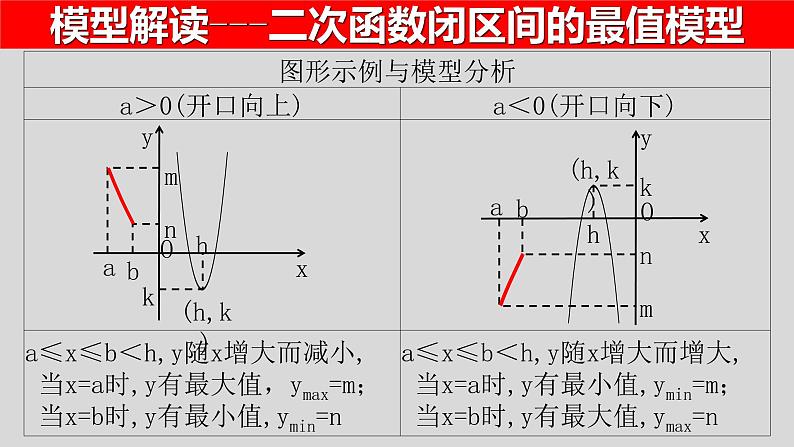
模型解读---二次函数闭区间的最值模型
典型例题---二次函数的闭区间最值模型
【例2】某超市以10元/件购进某种商品,(1)设该商品的销售单价为x(元/件)(11≤x≤19),在销售过程中发现,该商品的日销售量y(单位：件)与销售单价x之间存在一次函数关系,x,y之间的部分数值对应关系如右表.请写出y与x之间的函数关系式；(2)设该商品的日销售利润为w元,当该商品的销售单价x(元/件)定为多少时,日销售利润最大?最大利润时多少?
(1)y与x之间的函数关系式为y=-2x+40(11≤x≤19).
(2)根据题意，得w=(-2x+40)(x-10)=-2(x-15)2+50.(11≤x≤19)∵-2＜0,∴当x=15时，wmax=50.∴当甲商品的销售单价定为15元/件时,日销售利润最大,最大利润时50元。
1.如图1放置两个全等的含有30º角的直角三角板ABC与DEF(∠B=∠E=30º),若将三角板ABC向右以每秒1个单位长度的速度移动(点C与点E重合时移动终止),移动过程中始终保持点B,F,C,E在同一条直线上,如图2,AB与DF,DE分别交于点P,M,AC与DE交于点Q,其中AC=DE= ,设三角板ABC移动时间为xs.(1)在移动过程中,试用含x的代数式表示△AMQ的面积；(2)计算x等于多少时,两个三角板重叠部分的面积有最大值,最大值是多少?
当堂训练---二次函数闭区间的最值模型
模型解读---二次函数动点形成长度最值模型
典型例题---长度的最值问题
【例3】如图直线y=x与抛物线y=x2-2x-3交于点E、F,直线MN∥y轴,交直线y=x于点N,交抛物线于点M.(1)若点M为于点N的下方,求当MN最长时,M的坐标；(2)若以O、C、M、N为顶点的四边形是平行四边形, 求点M的坐标。
当堂训练---长度的最值问题
1.如图抛物线y1=x2-2x-3与抛物线y2=-x2-2x+3交于点A、B,直线MN∥y轴,分别交抛物线y1、y2于点M、N两点,且点M为点N的下方，求当MN最长时,M的坐标；
【例4-1】如图,在平面直角坐标系中,抛物线y=ax2+bx-3交x轴于A,B两点,交y轴于点C,且OA=OC=3OB.点P是第三象限内抛物线上的一动点.(1)求此抛物线的表达式；(2)求△PAC面积的最大值及此时点P的坐标.
(1)y=x2+2x-3
典型例题---面积的最值问题
(2)△PAC面积的最大值为27/8,(-3/2,-15/4)
模型解读---二次函数动点形成面积最值模型
【例4-2】如图,抛物线y=-x2-2x+3与x轴交于点A,B(点A在点B的左侧)，D(-2,y)是抛物线上一点,P为直线BE上方抛物线上一动点,设点P的横坐标为m.当m为何值时,△PBE的面积最大？
S△PAC=S△PBH+S△PDH-S△BDH =-1.5(m+0.5)2+27/8