专题03 用待定系数法确定二次函数的表达式-2021-2022学年九年级数学下册期末综合复习专题提优训练（苏科版）

2021-2022学年九年级数学下册期末综合复习专题提优训练（苏科版）

专题03 用待定系数法确定二次函数的表达式

【典型例题】

1．（2020·陆丰市甲东中学初三月考）已知抛物线经过点（1，0），（0，）．

（1）求该抛物线的函数表达式；

（2）抛物线可以由抛物线怎样平移得到？请写出一种平移的方法．

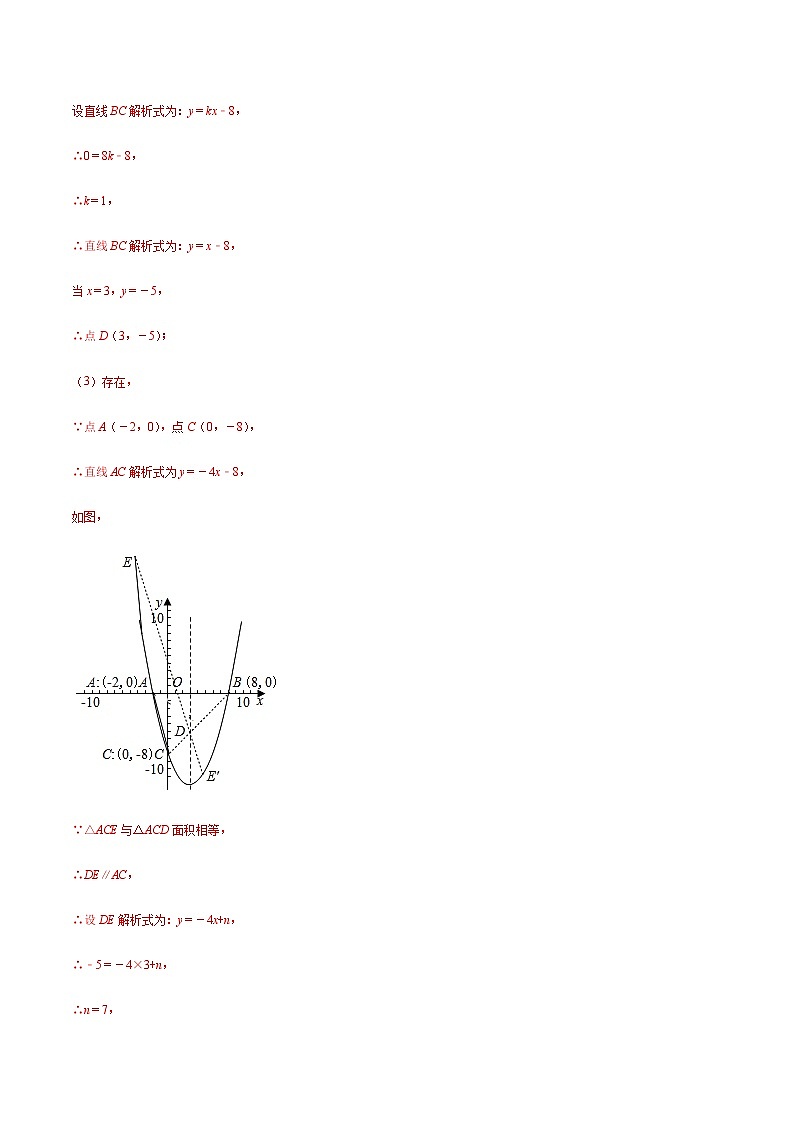
2．（2020·山东日照·二模）如图，二次函数y＝ax2+bx+c的图象与x轴交于点A(﹣2，0)和点B(8，0)，与y轴交于点C(0，﹣8)，连接AC，D是抛物线对称轴上一动点，连接AD，CD，得到△ACD．

（1）求该抛物线的函数解析式．

（2）△ACD周长能否取得最小值，如果能，请求出D点的坐标；如果不能，请说明理由．

（3）在（2）的条件下，在抛物线上是否存在点E，使得△ACE与△ACD面积相等，如果存在，请求出点的坐标；如果不存在，请说明理由．

【专题训练】

一、选择题

1．（2020·全国初三课时练习）如图，抛物线的表达式是（    ）

A．y＝x2－x＋2     B．y＝x2＋x＋2     C．y＝－x2－x＋2      D．y＝－x2＋x＋2

2．（2021·福建龙岩二中初三月考）已知抛物线经过(-2,n)和(4,n)两点，则n的值为（  ）

A．-2 B．-4 C．12 D．4

3．（2020·浙江温州·初三月考）已知一个二次函数的图象经过（-2，8），则下列点中在该函数的图象上的是（    ）

A．（2，8）， B．（1，3） C．（-1，3） D．（2，6）

4．（2020·河南洛宁·初三月考）一抛物线和抛物线y＝－2x2的形状、开口方向完全相同，顶点坐标是(－1，3)，则该抛物线的解析式为（    ）

A．y＝－2(x－1)2＋3 B．y＝－2(x＋1)2＋3

C．y＝－(2x＋1)2＋3 D．y＝－(2x－1)2＋3

5．（2020·上海嘉定·初三一模）如果A(-2，n)，B(2，n),C(4，n+12)这三个点都在同一个函数的图像上，那么这个函数的解析式可能是 (    )

A． B． C． D．

6．（2018·全国初三单元测试）一个二次函数的图象的顶点坐标为(3,-1)，与y轴的交点(0,-4)，这个二次函数的解析式是（                ）

A． B．

C． D．

7．（2020·巩义市回郭镇第一初级中学初三月考）2011年5月22日—29日在美丽的青岛市举行了苏迪曼杯羽毛球混合团体锦标赛．在比赛中，某次羽毛球的运动路线可以看作是抛物线y=－x2+bx+c的一部分（如图），其中出球点B离地面O点的距离是1m，球落地点A到O点的距离是4m，那么这条抛物线的解析式是（   ）

A．     B．   C．   D．

二、填空题

8．（2020·上海市静安区实验中学初三课时练习）抛物线经过点（2，-12），则c=_____________．

9．（2021·湖北麻城·思源实验学校初三月考）已知二次函数y＝ax2的图象经过点A(-2，)．则该函数的解析式为________.

10．（2020·全国初三课时练习）已知二次函数的图象过(0,1),(1,0),(-2,0)三点，则二次函数的解析式是__________．

11．（2020·东莞市长安实验中学月考）已知二次函数的图像经过（0，3），（-3，0），（2，-5），则二次函数的解析式为_______

12．（2020·福建泉州外国语学校初三月考）已知二次函数图象的顶点坐标为（1，﹣3），且过点（2，0），则这个二次函数的解析式_____．

13．（2020·巩义市回郭镇第一初级中学初三月考）某二次函数的图象与x轴交于点（﹣1，0），（4，0），且它的形状与y＝﹣x2形状相同．则这个二次函数的解析式为_____．

14．（2020·浙江绍兴·初三月考）如图，已知抛物线y=﹣x2+bx+c的对称轴为直线x=1，且与x轴的一个交点为（3，0），那么它对应的函数解析式是__．

三、解答题

15．（2020·黑龙江依安·期末）如图，抛物线y=ax2+bx+c (a≠0)过点M(-2，3)，顶点坐标为N(-1，4)，且与x轴交于A、B两点，与y轴交于C点．

（1）求抛物线的解析式；

（2）点P为抛物线对称轴上的动点，当PM+PB的值最小时，求点P的坐标；

16．（2020·吉林临江·期末）如图，已知直线y=x+3与x轴、y轴分别交于点A、B，抛物线y=-x2+bx+c经过A、B两点，与x轴交于另一个点C，对称轴与直线AB交于点E，抛物线顶点为D．

（1）求抛物线的解析式和顶点坐标；

（2）在第三象限内的抛物线上是否存在一点F，使A、E、C、F为顶点的四边形面积为6？若存在，直接写出点F的坐标；若不存在，说明理由．

17．（2020·杭州市实验外国语学校初三月考）如图，抛物线与轴交于和两点，交轴于点E．

（1）求此抛物线的解析式．

（2）若直线与抛物线交于A、D两点，与轴交于点，连接DE，求的面积．

18．（2020·北大附属台州书生学校月考）如图，抛物线与x轴交于点A(﹣1，0)，B(3，0)两点，直线与y轴交于点C，与x轴交于点D．点P是x轴上方的抛物线上一动点，过点P作PF⊥x轴于点F，交直线CD于点E．设点P的横坐标为m．

（1）求抛物线的解析式；

（2）若PE＝2EF，求m的值；

（3）若点是点F关于直线OE的对称点，是否存在点P，使点落在CD上？若存在，请直接写出相应的点P的坐标；若不存在，请说明理由．

19．（2020·辽宁绥中·初三二模）如图，二次函数的图象过点A(3,0)和B(-1,0)，与y轴交于点C．

（1）求该二次函数的解析式；

（2）若在该二次函数的对称轴上有一点M，使BM+CM的长度最短，求出M的坐标．

（3）动点D，E同时从点O出发，其中点D以每秒个单位长度的速度沿折线OAC按的路线运动，点E以每秒4个单位长度的速度沿折线OCA按的路线运动，当D，E两点相遇时，它们都停止运动．设D，E同时从点O出发t秒时，△ODE的面积为S．请直接写出S关于t的函数关系式，并写出自变量t的取值范围．

20．（2020·浙江省鄞州区宋诏桥中学初三一模）如图，抛物线y=ax2+bx(a＜0）过点E(10,0)，矩形ABCD的边AB在线段OE上（点A在点B的左边），点C，D在抛物线上．设A(t,0)，当t=2时，AD=4．

（1）求抛物线的函数表达式．

（2）当t为何值时，矩形ABCD的周长有最大值？最大值是多少？

（3）保持t=2时的矩形ABCD不动，向右平移抛物线．当平移后的抛物线与矩形的边有两个交点G，H，且直线GH平分矩形的面积时，求抛物线平移的距离．

21．（2020·武汉市光谷实验中学初三月考）如图，抛物线L：y=2x2-5x﹣12与x轴正半轴交于点A，与y轴交于点B．

（1）求直线AB的解析式及抛物线顶点坐标；

（2）如图1，点P为第四象限且在对称轴右侧抛物线上一动点，过点P作PC⊥x轴，垂足为C，PC交AB于点D，求PD+BD的最大值，并求出此时点P的坐标；

（3）如图2，将抛物线L：y=2x2-5x﹣12向右平移得到抛物线，直线AB与抛物线交于M，N两点，若点A是线段MN的中点，求抛物线的解析式．