沪科版九年级下册第24章 圆24.3 圆周角24.3.1 圆周角定理授课ppt课件

这是一份沪科版九年级下册第24章 圆24.3 圆周角24.3.1 圆周角定理授课ppt课件，共19页。PPT课件主要包含了情境导入，复习引课，圆心角的定义，知识精讲，类比圆心角探知圆周角，圆周角和圆心角的关系，∵OAOB，∴∠2∠3，∴∠12∠2，∴∠A∠ABO等内容，欢迎下载使用。

答：在同圆（或等圆）中，如果圆心角、弧、弦有其中的一组量相等，那么它们所对应的其余两个量都分别相等.
答:顶点在圆心的角叫圆心角.
2.上节课我们学习了一个反映圆心角、弧、弦三个量之间关系的一个结论，这个结论是什么？
一个三角形，当它内接于一个圆时，它的任一个角都与圆有着特殊的位置关系.如图，∆ABC内接于⊙O，这时∠A的定点在圆上，∠A的两边AB,AC分别与圆还有另一个公共点.
像这样，定点在圆上，并且两边都与圆还有另一个公共点的角叫做圆周角.
在同圆或等圆中,同弧或等弧所对的圆心角相等.
在同圆或等圆中,同弧或等弧所对的圆周角有什么关系？
为了解决这个问题,我们先探究同弧所对的圆周角和圆心角之间的关系.
你会画同弧所对的圆周角和圆心角吗?
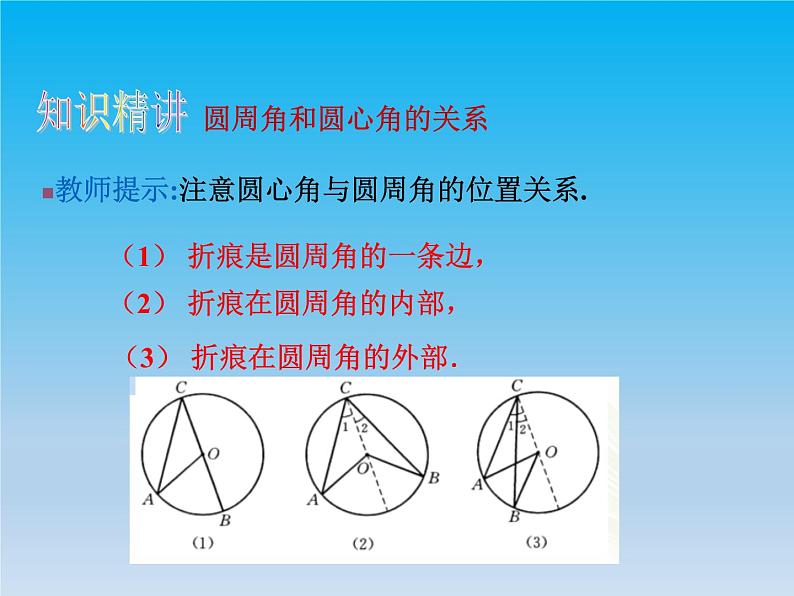
教师提示:注意圆心角与圆周角的位置关系.
（1） 折痕是圆周角的一条边，
（2） 折痕在圆周角的内部，
（3） 折痕在圆周角的外部．
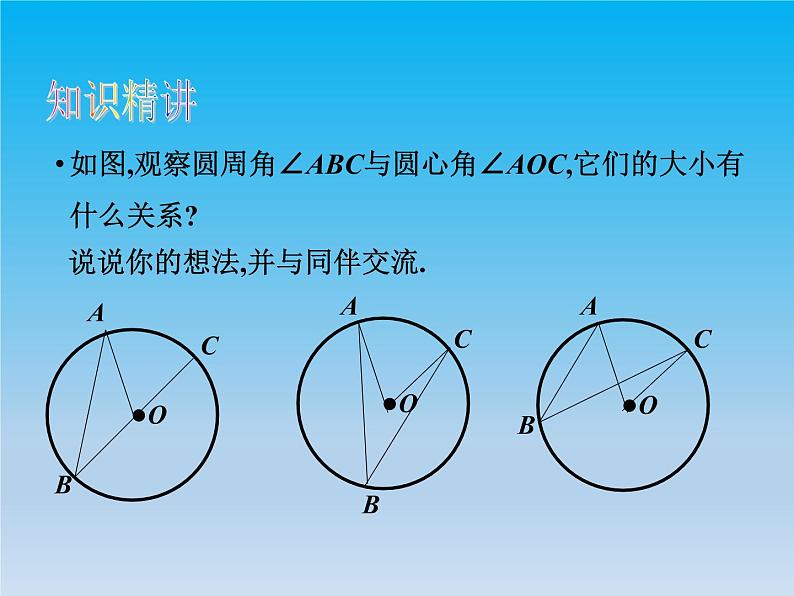
如图,观察圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系?
说说你的想法,并与同伴交流.
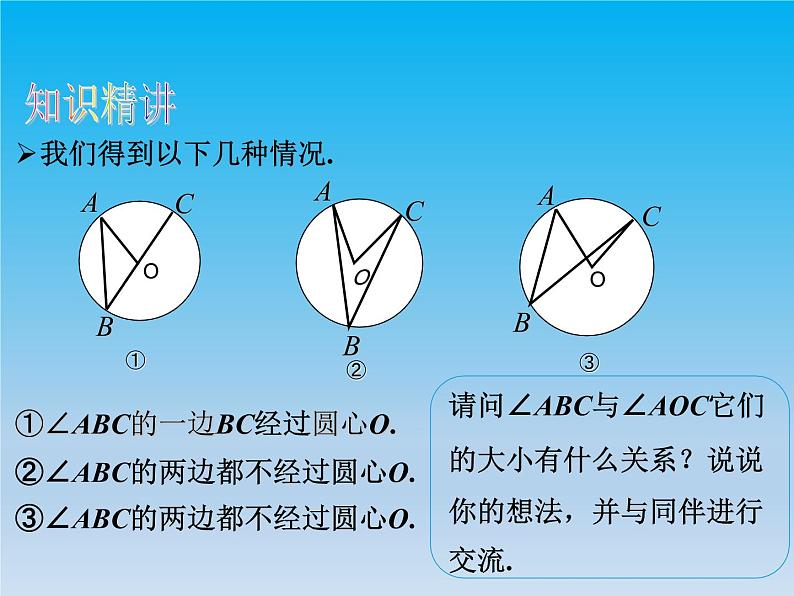
我们得到以下几种情况.
①∠ABC的一边BC经过圆心O.
②∠ABC的两边都不经过圆心O.
③∠ABC的两边都不经过圆心O.
请问∠ABC与∠AOC它们的大小有什么关系？说说你的想法，并与同伴进行交流.
下面我们首先考虑同学们列举的一种特殊情况，即∠ABC的一边BC经过圆心O.
∵ ∠AOC是△ABO的外角，
∴ ∠AOC=∠ABO+∠BAO.
∴ ∠ABO=∠BAO.
∴ ∠AOC=2∠ABO，
那么当∠ABC的两边都不经过圆心O时，∠ABC与∠AOC又有怎样的大小关系呢？
我们可以考虑把这两种情况分别转化成刚才的特殊情形来考虑.
也就是借用直径，连接BO并延长，与圆相交于点D.
（此时我们得到与图①同样的情形）
∵ ∠1是△ABO的外角，
∴ ∠1=∠2+∠3.
如图，连接BO并延长，与圆相交于点D.（此时我们得到与图①同样的情形）
∵ ∠AOD是△ABO的外角,
∴ ∠AOD=∠A+∠ABO.
∴ ∠AOD=2∠ABD ,
如图，连接BO并延长，与相交于点D.（此时我们得到与图①同样的情形）
∴ ∠ABD=∠A+∠ABO.
如图，连接BO并延长，与圆O相交于点D.（此时我们得到与图①同样的情形）
通过对三种情形的证明，同学们再认真观察图形，你会得到什么结果？
一条弧所对的圆周角等于它所对的圆心角的 .
推论 1 在同圆或者等圆中，同弧或等弧所对的圆周角相等，相等的圆周角所对的弧也相等（图 24-36）.
推论 2 半圆或直径所对的圆周角是直角；90°的圆周角所对的弦是直径（图 24-37）.
例1 如图24-38，AB为⊙O的直径，弦CD交AB于点P，∠ACD=60°，∠ADC=70°，求∠APC的度数.
解：连接BC，则∠ACB=90°,
∠DCB=∠ACB-∠ACD=30°.
∴ ∠APC =∠BAD+∠ADC=30°+70°=100°.
分析：∠APC等于圆周角∠BAD与∠ADC之和.
又 ∵ ∠BAD=∠DCB=30°，
如图，在⊙O中，∠BOC=50°，则∠BAC= .
变化题2：如图，∠BAC=40°，则∠OBC= .
变化题1：如图，点A，B，C是⊙O上的三点， ∠BAC=40°，则∠BOC= .
如图，OA，OB，OC都是⊙O的半径，∠ AOB=2∠ BOC，∠ ACB与∠ BAC的大小有什么关系？为什么？
解：∠ACB=2∠BAC.理由:
∵ ∠AOB=2∠ACB,
∠BOC=2∠BAC,
∠AOB=2∠BOC,
∴ 2∠ACB =2（2∠BAC）.
∴∠ACB=2∠BAC.