专题02 翻折、直尺、三角板中的平行问题-2021-2022学年七年级数学下册解法技巧思维培优（人教版）

这是一份专题02 翻折、直尺、三角板中的平行问题-2021-2022学年七年级数学下册解法技巧思维培优（人教版），文件包含专题02翻折直尺三角板中的平行问题解析版docx、专题02翻折直尺三角板中的平行问题原卷版docx等2份试卷配套教学资源，其中试卷共17页， 欢迎下载使用。

典例题型一 翻折与平行线
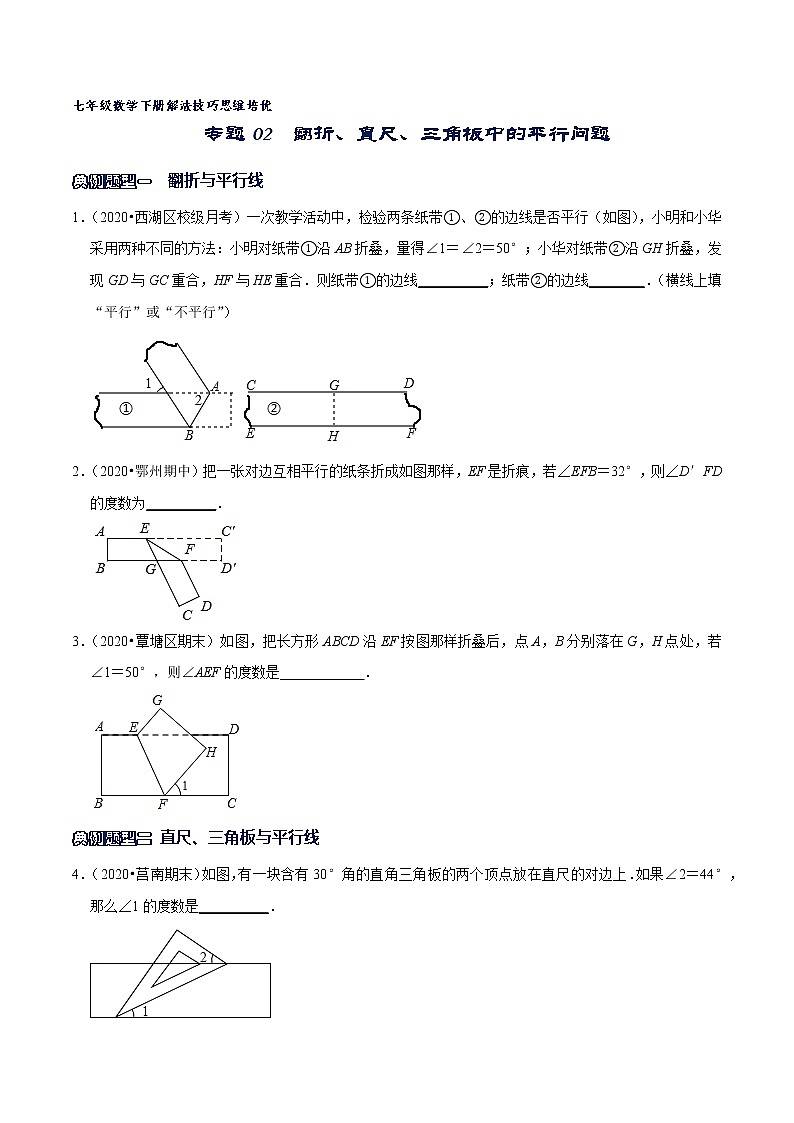
1．（2020•西湖区校级月考）一次教学活动中，检验两条纸带①、②的边线是否平行（如图），小明和小华采用两种不同的方法：小明对纸带①沿AB折叠，量得∠1＝∠2＝50°；小华对纸带②沿GH折叠，发现GD与GC重合，HF与HE重合．则纸带①的边线__________；纸带②的边线________．（横线上填“平行”或“不平行”）
2．（2020•鄂州期中）把一张对边互相平行的纸条折成如图那样，EF是折痕，若∠EFB＝32°，则∠D′FD的度数为__________．
3．（2020•覃塘区期末）如图，把长方形ABCD沿EF按图那样折叠后，点A，B分别落在G，H点处，若∠1＝50°，则∠AEF的度数是____________．
典例题型二 直尺、三角板与平行线
4．（2020•莒南期末）如图，有一块含有30°角的直角三角板的两个顶点放在直尺的对边上．如果∠2＝44°，那么∠1的度数是__________．
5．（2020•孟津期末）如图，将三角板与直尺贴在一起，使三角板的直角顶点C（∠ACB＝90°）在直尺的一边上，若∠2＝65°，则∠1的度数是（ ）
A．15°B．25°C．35°D．65°
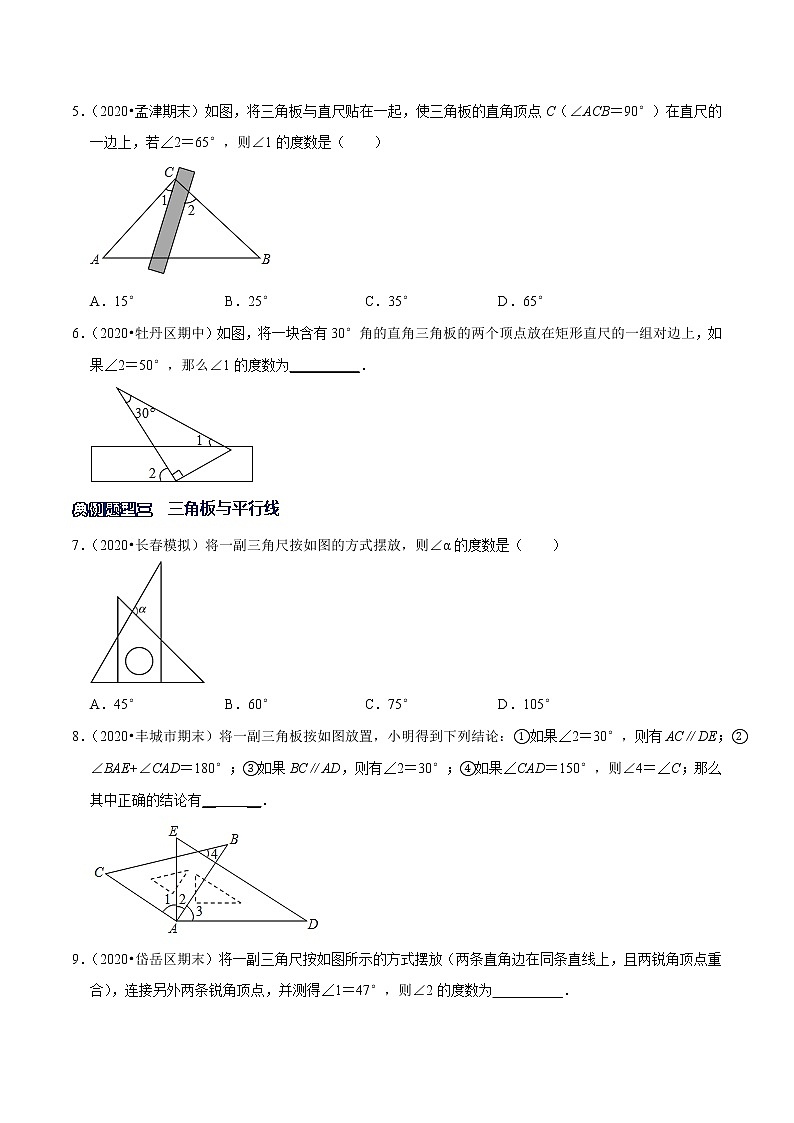
6．（2020•牡丹区期中）如图，将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上，如果∠2＝50°，那么∠1的度数为__________．
典例题型三 三角板与平行线
7．（2020•长春模拟）将一副三角尺按如图的方式摆放，则∠α的度数是（ ）
A．45°B．60°C．75°D．105°
8．（2020•丰城市期末）将一副三角板按如图放置，小明得到下列结论：①如果∠2＝30°，则有AC∥DE；②∠BAE+∠CAD＝180°；③如果BC∥AD，则有∠2＝30°；④如果∠CAD＝150°，则∠4＝∠C；那么其中正确的结论有__________．
9．（2020•岱岳区期末）将一副三角尺按如图所示的方式摆放（两条直角边在同条直线上，且两锐角顶点重合），连接另外两条锐角顶点，并测得∠1＝47°，则∠2的度数为__________．
巩固练习
1．（2020•长春模拟）如图，将一副三角板按如图放置，则下列结论：
①∠1＝∠3；
②如果∠2＝30°，则有BC∥AE；
③如果∠1＝∠2＝∠3，则有BC∥AE；
④如果∠2＝45°，必有∠4＝∠E．
其中正确的有（ ）
A．①②B．①③C．①②④D．①③④
2．（2020•烟台）小明将一张正方形纸片按如图所示顺序折叠成纸飞机，当机翼展开在同一平面时（机翼间无缝隙），∠AOB的度数是________．
3．（2020•苏州期末）将一张长方形纸条折成如图所示的图形，如果∠1＝64°，那么∠2＝__________．
4．（2020•遂宁期末）如图，把一张长方形纸片ABCD沿EF折叠，若∠EFG＝52°，则∠AEG的度数是__________．
5．（2020•东至期末）如图，将一张长方形纸条折叠，若∠1＝52°，则∠2＝__________．
6．（2020•河西区期中）如图，一副直角三角板技如图所示的方式摆放，其中点C在FD的延长线上，且AB∥FC，则∠CBD的度数为__________．
7．（2020•沙坪坝区校级期末）将一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G、D、C分别在M、N的位置上，若∠EFG＝52°，则∠2﹣∠1＝____________°．
8．（2020•诸城市期末）如图（1）是长方形纸带，∠DEF＝20°，将纸带沿EF折叠图（2）形状，则∠FGD等于__________度．
9．（2020•南昌期末）将三角尺的直角顶点放在直尺的一边上，若∠1＝30°，∠2＝56°，则∠3的度数是____________．
10．（2020•泉州期末）如图，将一张长方形纸条沿某条直线折叠，若∠1＝116°，则∠2等于__________．