

陕西省西安中学2022届高三第二次模拟考试数学(理)试题(含答案)
展开陕西省西安中学高2022届高三第二次模拟考试
理科数学试题
第Ⅰ卷(选择题 共60分)
一、选择题:(本题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.已知复数满足(其中为虚数单位),则复数的虚部为
A. B. C.1 D.
2.某几何体的三视图如图所示(单位:,则该几何体的体积(单位:是
A.2 B.4 C.6 D.8
3.的展开式中,第5项为常数项,则
A.8 B.6 C.7 D.10
4.已知各项均为正数的等比数列的前4项和为15,且,则
A.16 B.8 C.4 D.2
5.现有语文、数学、英语、物理各1本书,把这4本书分别放入3个不同的抽屉里,要求每个抽屉至少放一本书且语文和数学不在同一个抽屉里,则放法数为
A.18 B.24 C.30 D.36
6.在数学的研究性学习中,常利用函数的图象研究函数的性质,也利用函数的解析式研究函数的性质,下列函数的解析式(其中为自然对数的底数)与所给图象最契合的是
A. B. C. D.
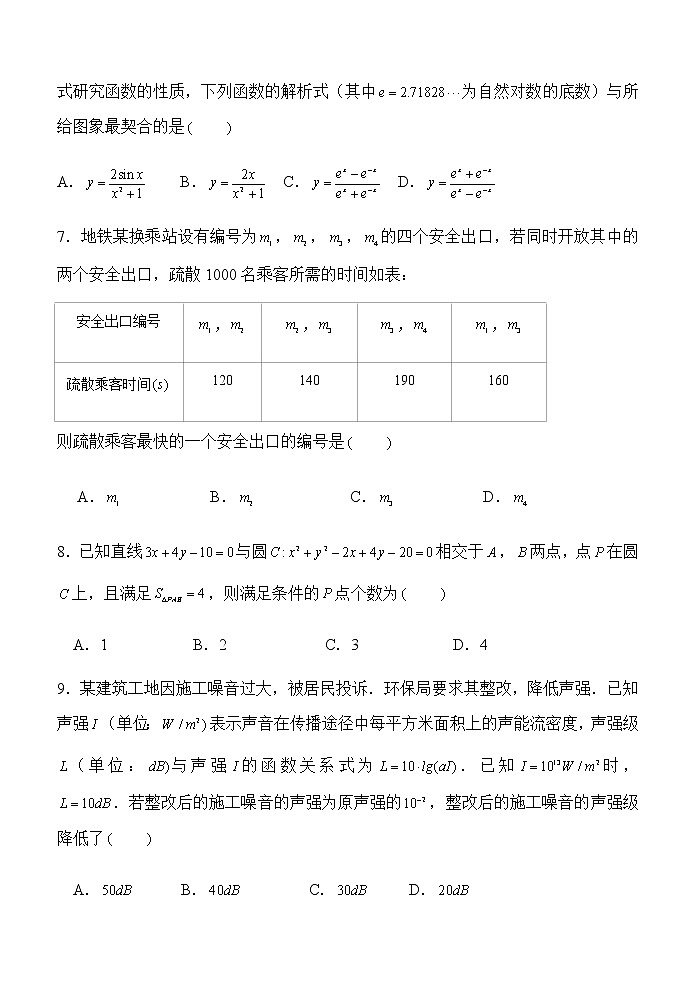
7.地铁某换乘站设有编号为,,,的四个安全出口,若同时开放其中的两个安全出口,疏散1000名乘客所需的时间如表:
安全出口编号 | , | , | , | , |
疏散乘客时间 | 120 | 140 | 190 | 160 |
则疏散乘客最快的一个安全出口的编号是
A. B. C. D.
8.已知直线与圆相交于,两点,点在圆上,且满足,则满足条件的点个数为
A.1 B.2 C.3 D.4
9.某建筑工地因施工噪音过大,被居民投诉.环保局要求其整改,降低声强.已知声强(单位:表示声音在传播途径中每平方米面积上的声能流密度,声强级(单位:与声强的函数关系式为.已知时,.若整改后的施工噪音的声强为原声强的,整改后的施工噪音的声强级降低了
A. B. C. D.
10.已知双曲线的上、下顶点分别为,,点在双曲线上(异于顶点),直线,的斜率乘积为,则双曲线的渐近线方程为
A. B. C. D.
11.已知函数,若方程有三个不等根,,,则的取值范围是
A. B. C. D.
12.已知数列满足,,则数列的前40项和
A. B. C. D.
第Ⅱ卷(非选择题 共90分)
二、填空题 (本题共4小题,每小题5分,共20分)
13.已知单位向量,满足,则与的夹角为 .
14.被誉为“中国现代数学之父”的著名数学家华罗庚先生为我国数学的发展做出了巨大贡献,他所倡导的“0.618优选法”在生产和科研实践中得到了广泛的应用就是黄金分割比的近似值,黄金分割比还可以表示成,则 .
15.如图所示,已知抛物线的焦点为,准线与轴的交点为,点在抛物线上,且在轴的上方,过点作于,,则的面积为 .
16.已知在圆柱(,是圆柱上下底面圆心)内有一个球,该球与圆柱的上、下底面及母线均相切.过直线的平面截圆柱得到四边形,其面积为8.若为圆柱底面圆弧的中点,则平面与球的交线长为 .
三、解答题:(共70分.解答应写出文字说明、证明过程或演算步骤.)
17.(本小题满分12分)请从下面三个条件中任选一个,补充在下面的横线上,并解答.①2sin(A+C)+2sin(B+C)cos(A+B)=sin(A+B);
②tanA+tanB+tanC﹣tanBtanC=0;
③cosA(bcosA+acosB)﹣csinA=0,
已知△ABC中的内角A,B,C的对边分别为a,b,c,_____.
(1)求A;(2)若a+2b=3且a2bc,求△ABC的面积.
18.(本小题满分12分)在三棱锥中,底面为正三角形,平面平面,,为上一点,,为三角形的中心.
(1)求证:平面;
(2)若直线与平面所成的角为,求二面角的余弦值.
19.(本小题满分12分)天文学上用星等表示星体亮度,星等的数值越小、星体越亮.视星等是指观测者用肉眼所看到的星体亮度;绝对星等是假定把恒星放在距地球32.6光年的地方测得的恒星的亮度,反映恒星的真实发光本领.如表列出了(除太阳外)视星等数值最小的10颗最亮恒星的相关数据,其中,.
星名 | 天狼星 | 老人星 | 南门二 | 大角星 | 织女一 | 五车二 | 参宿七 | 南河三 | 水委一 | 参宿四 |
视星等 | 0.03 | 0.08 | 0.12 | 0.38 | 0.46 | |||||
绝对星等 | 1.42 | 4.4 | 0.6 | 0.1 | 2.67 | |||||
赤纬 |
(1)从表中随机选择一颗恒星,求它的绝对星等的数值小于视星等的数值的概率;(2)已知北京的纬度是北纬,当且仅当一颗恒星的“赤纬”数值大于时,能在北京的夜空中看到它,现从这10颗恒星中随机选择4颗,记其中能在北京的夜空中看到的数量为颗,求的分布列和数学期望;
(3)记时10颗恒星的视星等的方差为,记时10颗恒星的视星等的方差为,判断与之间的大小关系.(写结论不需要证明)
20.(本小题满分12分)已知椭圆的左、右焦点分别为、,是椭圆上的一动点,且的最小值是1,当垂直长轴时,.
(1)求椭圆的方程;
(2)是否存在斜率为的直线与以线段为直径的圆相交于、两点,与椭圆相交于、两点,且?若存在,求出直线的方程;若不存在,说明理由.
21.(本小题满分12分)已知函数.
(Ⅰ)求曲线在点,(1)处的切线方程;
(Ⅱ)求的单调区间;
(Ⅲ)若关于的方程有两个不相等的实数根,记较小的实数根为,
求证:.
选做题:请考生在第22、23二题中任意选一题作答,如果多做,则按所做的第一题记分.作答时,用铅笔在答题卡上把所选题目对应的题号涂黑.
22.(本小题满分10分)已知在平面直角坐标系中,曲线的参数方程为为参数).以原点为极点,轴正半轴为极轴建立极坐标系,直线的极坐标方程为.
(1)求曲线和直线的直角坐标方程;
(2)若直线交曲线于,两点,交轴于点,求的值.
23.(本小题满分10分)已知函数f(x)=|ax+1|+|3x﹣1|.
(1)当a=3时,求不等式f(x)>3的解集;
(2)若0<a<3,且对任意的x∈R,f(x)≥恒成立,求a的最小值.
陕西省西安中学高2022届高三第二次模拟考试
理科数学答案
一、选择题 1-5 ACBCC 6-10 BBDDB 11-12 CA
二、填空题 . 2 . 8 . .
1.【解答】解:由,
得, 复数的虚部为. 故选:.
2.【解答】解:根据三视图:该几何体为底面为直角梯形的四棱柱.
如图所示:故该几何体的体积为:.故选:.
3.【解答】解:第5项为,由得,故选:.
4.【解答】解:设等比数列的公比为,则由前4项和为15,且,有
,,.故选:.
5.【解答】解:根据题意,分2步进行分析:①将4本书分为3组,语文和数学不在同一个组,有种分组方法,②将分好的3组分别放到个抽屉,有种安排方法,则有种放法,故选:.
6.【解答】解:函数的定义域为,排除,的定义域为,
当时,,排除,当,,,排除,故选:.
7.【解答】由同时开放,疏散1000名乘客所需的时间为,同时开放,疏散1000名乘客所需的时间为,所以比疏散乘客快,由同时开放,疏散1000名乘客所需的时间为,同时开放,疏散1000名乘客所需的时间为,所以比疏散乘客快,由同时开放,疏散1000名乘客所需的时间为,同时开放,疏散1000名乘客所需的时间为,所以比疏散乘客快,由同时开放,疏散1000名乘客所需的时间为,同时开放,疏散1000名乘客所需的时间为,所以比疏散乘客快,综上所述:,,,,所以疏散乘客最快的一个安全出的编号是,故选:.
8.【解答】解:圆化为,则圆心坐标为,半径,圆心到直线的距离,则弦长,设到的距离为,则,解得.而圆上两侧的动点到直线的最大距离分别为5和2,故满足条件的点共4个.故选:.
9.【解答】解:由题意可知,,当时,,有,解得,故有,当变为原声强的时,,有,可得,
由此可知降低了,故选:.
10.【解答】解:双曲线的上、下顶点分别为,,
点是上异于,的一点,可得,即有,
设直线,的斜率分别为,,直线,的斜率乘积为,即.所以,则的渐近线方程为,故选:.
11.【解答】解:因为函数,
作出函数的图象如图所示,由图可知,,设,则,所以,又,所以,,又,故的取值范围是.故选:.
12.【解答】解:数列满足,,
,,
,.
.
则数列的前40项和.故选:.
13.【解答】解:,,,解得,
,且,
14.【解答】解:由题意,,,
则.故答案为:2.
15.【解答】解:因为抛物线的焦点,所以的坐标,准线为,
因为抛物线的准线与轴的交点为,所以,可设,,
则,,,因为,
所以,解得或(舍去),
可得,,可知为等腰直角三角形,且,所以.
16.
三、解答题:
17.【解答】解:(1)选①,2sin(A+C)+2sin(B+C)cos(A+B)=sin(A+B),
由诱导公式,得2sin(A+C)﹣2sinA cosC=sinC,即2sinC cosA=sinC,
因为sinC≠0,所以,所以
选②,由诱导公式,得,整理即有tanA+tanB+tanC﹣tanAtanBtanC=0,
又已知,且tanAtanBtanC≠0,所以,所以.
选③,已知,
由正弦定理,可得,
所以,即,
因为sinC≠0,所以,即,所以.
(2)因为a2≤bc,所以由余弦定理,有a2=b2+c2﹣2bccosA=b2+c2﹣bc≤bc,所以(b﹣c)2≤0,所以b=c,又,所以a=b=c,所以△ABC为等边三角形.又因为a+2b=3,所以a=b=1,
所以.
18.【解答】(1)证明:连结并延长交于点,则为的中点,连结,如图所示,因为为正三角形的中心,所以,又,所以,因为,为的中点,所以,又平面平面,平面平面,平面,
所以平面,所以平面,又平面,所以,
又,,,平面,所以平面;
(2)解:由平面可知,,所以,所以,
所以,由(1)可知,,,两两垂直,
所以分别以,,所在直线为轴,轴,轴,建立空间直角坐标系如图所示,
则,所以,
设平面的法向量为,则,令,则,所以,由(1)可知,平面,故为平面的法向量,
,二面角为锐二面角,二面角的余弦值为.
19.【解答】解:(Ⅰ)设一颗星的绝对星等的数值小于视星等的数值为事件.,
由图表可知,10颗恒星有5颗恒星绝对星等的数值小于视星等的数值,所以;
(Ⅱ)由图表知,有7颗恒星的“赤纬”数值大于,有3颗恒星的“赤纬”数值小于.,
所以随机变量的所有可能取值为:1,2,3,4,
,,,,
所以随机变量的分布列为:
1 | 2 | 3 | 4 | |
所以的数学期望为; (Ⅲ)结论:.
20.【解答】解:(1)由题意,点是椭圆上的一个动点,且的最小值为1,得,
因为当垂直长轴时,,所以,即,
又由,解得,,所以椭圆的标准方程为.
(2)假设存在斜率为的直线,设为,由(1)知,,,所以以线段为直径的圆为,由题意,圆心到直线的距离,得,所以,联立,得,
由题意,△,解得,又,所以,
设,,,,则,,
所以,
若,则,
所以,解得,或,又,所以,即,
故存在符合条件的直线,其方程为或.
21.【解答】(Ⅰ)解:由,可得,则(1),又(1),
所以曲线在点,(1)处的切线方程为,即.
(Ⅱ)解:的定义域为,,
当时,,在上单调递增;
当时,令,可得,令,可得,
所以在上单调递减,在上单调递增.
(Ⅲ)证明:由(Ⅱ)可知,当时,才有两个不相等的实根,且,
则要证,即证,即证,而,则,否则方程不成立),所以即证,化简得,
令,则,当时,,单调递减,
当时,,单调递增,所以(1),而,
所以,所以,得证.
22.【解答】解:(1)曲线的参数方程为为参数),转换为,
整理得,①②转化为直角坐标方程为,
直线的极坐标方程,直角坐标方程为.
(2)由于直线与轴的交点坐标为,所以直线的参数方程为为参数),代入,得到,所以,,则.
23.【解答】解:(1)a=3时,函数f(x)=|3x+1|+|3x﹣1|=,不等式f(x)>3等价于或,解得x<﹣或x>,所以不等式f(x)>3的解集为(﹣∞,﹣)∪(,+∞);
(2)0<a<3时,f(x)=|ax+1|+|3x﹣1|=,
此时﹣(a+3)<0,﹣(3﹣a)<0,且a+3>0,所以对任意的x∈R,f(x)≥f()=a+1,
令a+1≥,化简得a2+3a﹣4≥0,解得a≥1或a≤﹣4(不合题意,舍去),
所以a≥1,即a的最小值是1.
2024届陕西省西安市西安中学高三上学期期中数学(理)试题含答案: 这是一份2024届陕西省西安市西安中学高三上学期期中数学(理)试题含答案,共20页。试卷主要包含了单选题,填空题,问答题,证明题,应用题,解答题等内容,欢迎下载使用。
2020西安中学高三第二次模拟考试数学(理)试题PDF版含答案: 这是一份2020西安中学高三第二次模拟考试数学(理)试题PDF版含答案
2020西安中学高三第八次模拟考试数学(理)试题含答案: 这是一份2020西安中学高三第八次模拟考试数学(理)试题含答案












