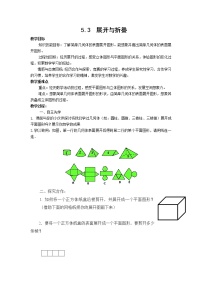
初中数学5.3 展开与折叠教学设计

这是一份初中数学5.3 展开与折叠教学设计，共4页。教案主要包含了四方成线两相卫，六种图形巧组合，跃马失蹄四分开，两两错开一阶梯，对面相隔不相连，识图巧排“ 7”等内容，欢迎下载使用。
七年级数学上册 5.3 展开与折叠巧记口诀确定正方体表面展开图素材新版苏科版 082311156 个相连的正方形组成的平面图形，经折叠能否围城正方体问题，是近年来中考常考题 型。同学们在学习这一知识时常感到无从下手， 现将确定正方体展开图的方法以口诀的方式总结出来，供大家参考：正方体盒巧展开，六个面儿七刀裁。十四条边布周围，十一类图记分明： 四方成线两相卫，六种图形巧组合； 跃马失蹄四分开；两两错开一阶梯。对面相隔不相连 , 识图巧排“ 7”、“凹”、“田”。 现将口诀的内涵解释如下：  将一个正方体盒的表面沿某些棱剪开，  展开成平面图形， 需剪 7 刀，故平面展开图中周围有 14 条边长共有十一种展开图：一、四方成线两相卫，六种图形巧组合        （ 1） （ 2） （ 3） （ 4）       （ 5） （ 6） 以上六种展开图可归结为四方连线， 即 ，另外两个小方块在四个方块的上下两侧，共六种情况。二、跃马失蹄四分开
（ 1） （ 2） （ 3） （ 4） 以上四种情况可归结为五个小方块组成“三二相连”的基本图形（如图） ，另外一个小方块的位置有四种情况，              即图中四个小方块中的任意一个，              这一图形有点像失蹄的马，              故称为“跃马失蹄”。  三、两两错开一阶梯 这一种图形是两个小方块一组，两两错开，像阶梯一样，故称“两两错开一阶梯”。    四、对面相隔不相连 这是确定展开图的又一种方法， 也是确定展开图中的对面的一种方法。 如果出现三个相连，则 1 号面与 3 号面是对面，中间隔了一个              2 号面，并且是对面的一定不相连。 1 2 3五、识图巧排“ 7”、“凹”、“田”   1 2 3 4 5    （ 1） （ 2） （ 3） 这里介绍的是一种排除法。 如果图中出现象图 （ 1）中的“ 7”形结构的图形不可能是正方体展开图的，因为图中              1 号面与 3 号面是对面， 3 号面又与 5 号面是对面，出现矛盾。如果图中出现象图（ 2）中的“田”形结构的图形不可能是正方体展开图的，因为同一 顶点处不可能出现四个面的。 如果图中出现象图（ 3）中的“凹”形结构的图形不可能是正方体展开图的，因为如果把该图形折叠起来将有两个面重合。现举例说明： 例 1．（ 2004 海口市实验区）下面的平面图形中，是正方体的平面展开图的是（ ）
         解析：本题可用“识图巧排  ‘7’、‘田’、‘凹’”来解决。 A、 D 都有“凹”形结构， B 有“田”形结构，故应选              C例 2．（ 2004  扬州）马小虎准备制作一个封闭的正方体  盒子，他先用  5  个大小一样的正方形制成如右图所示的拼接图形 ( 实线部分 ) ，经折叠后发现还少一个面，              请你在右图中的拼接图形上再接一个正方形，              使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子                            .( 注：①只需添加一个符合要求的正方形；②添加的正方形用阴影表示 .) 解析：本题可用“跃马失蹄四分开”来解决。图中具备了三二相连的结构，故本题有四种答案，即小方块的位置有图中所示的四种情况之一。试一试： 1．（ 2004 浙江金华）下列图形中，不是立方体表面展开图的是（ ）     2．（ 2004 镇江）如图，有一个正方体纸盒，在它的三个侧面分别画有三角形、正方形和圆，现用一把剪刀沿着它的棱剪开成一个平面图形，则展开图可以是（              ）          
（ 正方体纸盒 ）
（ A ） （ B ） （ C） （ D）
 3．（ 2004 海南） 如图是一个正方体包装盒的表面展开图， 若在其中的三个正方形 A、B、 C内分别填上适当的数，使得将这个表面展开图沿虚线折成正方体后，相对面上的两数互为相反数，则填在 A、B、C 内的三个数依次是（ ）．