所属成套资源:湘教版八下数学期末专项复习
湘教版八下数学 解题技巧专题:特殊平行四边形中的解题方法
展开
这是一份湘教版八下数学 解题技巧专题:特殊平行四边形中的解题方法,共4页。试卷主要包含了利用对称性求最值【方法10】,利用面积法求定值等内容,欢迎下载使用。
一、利用对称性求最值【方法10】
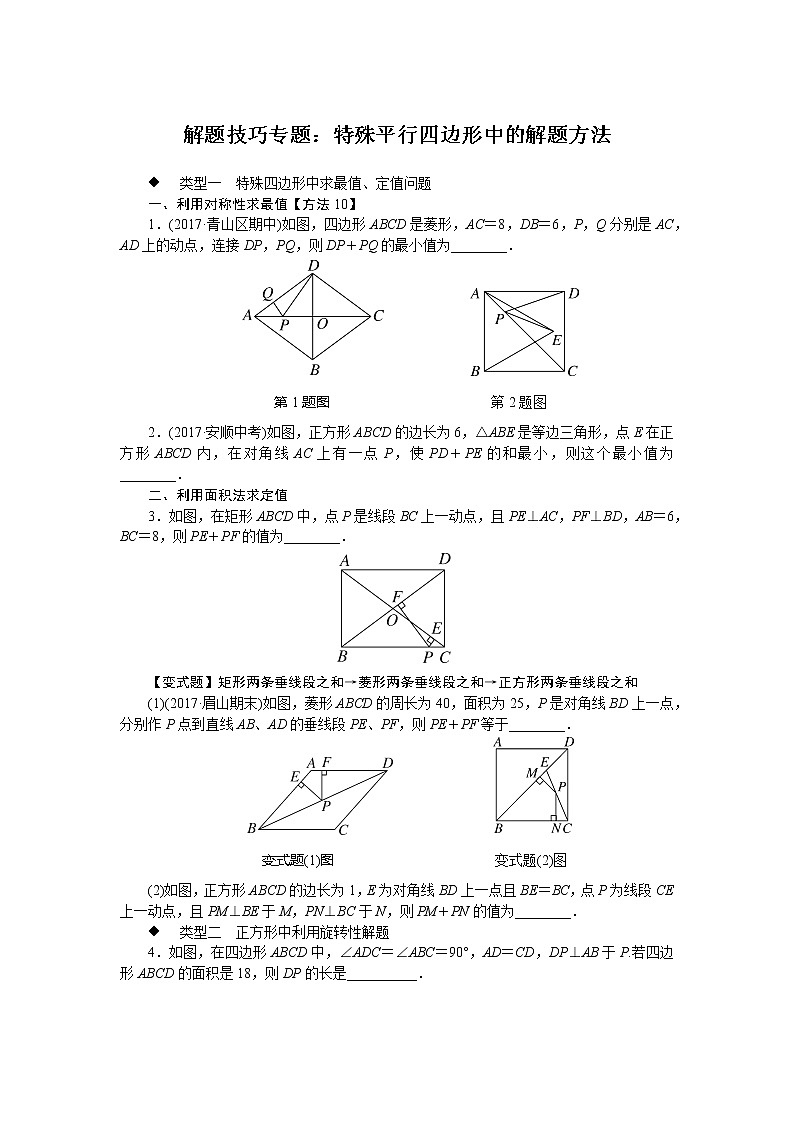
1.(2017·青山区期中)如图,四边形ABCD是菱形,AC=8,DB=6,P,Q分别是AC,AD上的动点,连接DP,PQ,则DP+PQ的最小值为________.
第1题图 第2题图
2.(2017·安顺中考)如图,正方形ABCD的边长为6,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为________.
二、利用面积法求定值
如图,在矩形ABCD中,点P是线段BC上一动点,且PE⊥AC,PF⊥BD,AB=6,BC=8,则PE+PF的值为________.
【变式题】矩形两条垂线段之和→菱形两条垂线段之和→正方形两条垂线段之和
(1)(2017·眉山期末)如图,菱形ABCD的周长为40,面积为25,P是对角线BD上一点,分别作P点到直线AB、AD的垂线段PE、PF,则PE+PF等于________.
变式题(1)图 变式题(2)图
(2)如图,正方形ABCD的边长为1,E为对角线BD上一点且BE=BC,点P为线段CE上一动点,且PM⊥BE于M,PN⊥BC于N,则PM+PN的值为________.
eq \a\vs4\al(◆)类型二 正方形中利用旋转性解题
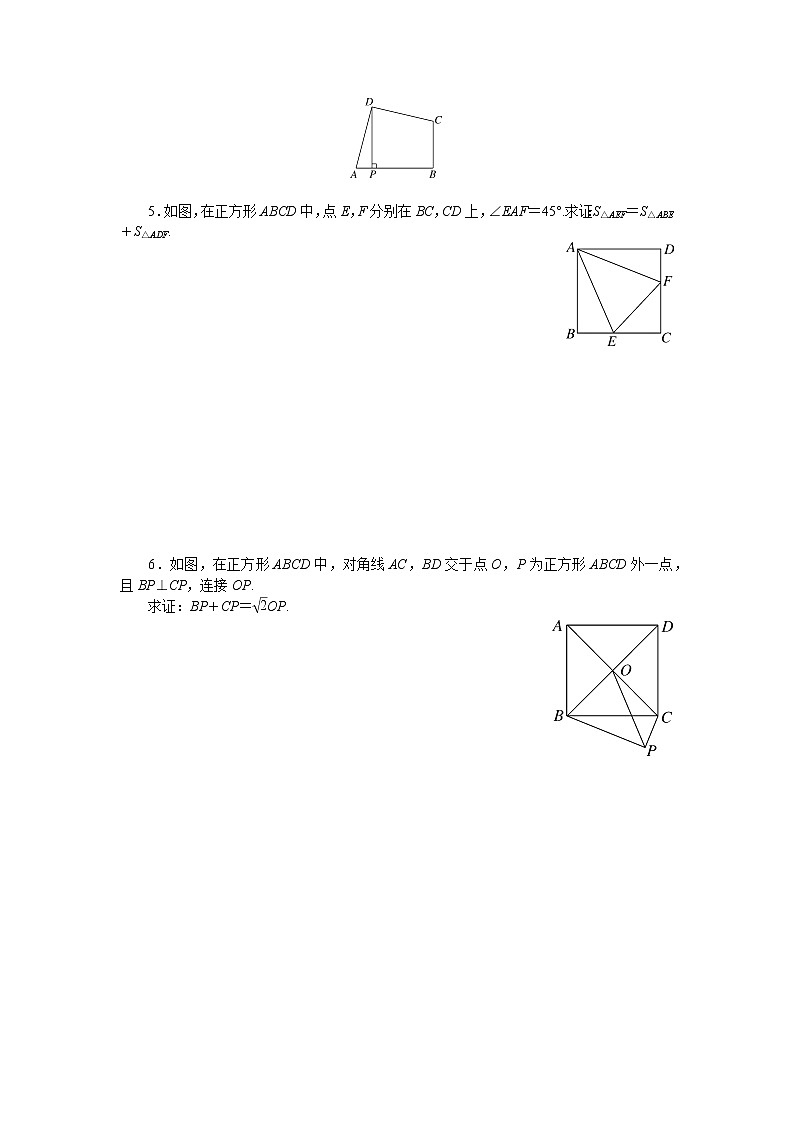
如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P.若四边形ABCD的面积是18,则DP的长是__________.
5.如图,在正方形ABCD中,点E,F分别在BC,CD上,∠EAF=45°.求证:S△AEF=S△ABE+S△ADF.
6.如图,在正方形ABCD中,对角线AC,BD交于点O,P为正方形ABCD外一点,且BP⊥CP,连接OP.
求证:BP+CP=eq \r(2)OP.
参考答案与解析
eq \f(24,5) 解析:如图,过点Q作QE⊥AC交AB于点E,则PQ=PE.∴DP+PQ=DP+PE.当点D,P,E三点共线的时候DP+PQ=DP+PE=DE最小,且DE即为所求.当DE⊥AB时,DE最小.∵四边形ABCD是菱形,∴AC⊥BD,OA=eq \f(1,2)AC=4,OB=eq \f(1,2)BD=3,∴AB=5.∵S菱形ABCD=eq \f(1,2)AC·BD=AB·DE,∴eq \f(1,2)×8×6=5·DE,∴DE=eq \f(24,5).∴DP+PQ的最小值为eq \f(24,5).
2.6 解析:如图,设BE与AC交于点P,连接BD.∵点B与D关于AC对称,∴PD=PB,∴PD+PE=PB+PE=BE,即P为AC与BE的交点时,PD+PE最小,为BE的长度.∵正方形ABCD的边长为6,∴AB=6.又∵△ABE是等边三角形,∴BE=AB=6.故所求最小值为6.故答案为6.
eq \f(24,5) 解析:∵四边形ABCD为矩形,∴∠ABC=90°.∵AB=6,BC=8,∴AC=10,∴OB=OC=eq \f(1,2)AC=5.如图,连接OP,∵S△OBP+S△OCP=S△OBC,∴eq \f(OB·PF,2)+eq \f(OC·PE,2)=S△OBC,∴eq \f(5·PF,2)+eq \f(5·PE,2)=S△OBC.∵S△OBC=eq \f(1,4)S矩形ABCD=eq \f(1,4)AB·BC=eq \f(1,4)×6×8=12,∴eq \f(5·PF,2)+eq \f(5·PE,2)=12,∴PE+PF=eq \f(24,5).
【变式题】(1)eq \f(5,2) 解析:∵菱形ABCD的周长为40,面积为25,∴AB=AD=10,S△ABD=eq \f(25,2).连接AP,则S△ABD=S△ABP+S△ADP,∴eq \f(1,2)×10(PE+PF)=eq \f(25,2),∴PE+PF=eq \f(5,2).
(2)eq \f(\r(2),2) 解析:连接BP,过点E作EH⊥BC于H.∵S△BPE+S△BPC=S△BEC,∴eq \f(BE·PM,2)+eq \f(BC·PN,2)=eq \f(BC·EH,2).又∵BE=BC,∴eq \f(PM,2)+eq \f(PN,2)=eq \f(EH,2),即PM+PN=EH.∵△BEH为等腰直角三角形,且BE=BC=1,∴EH=eq \f(\r(2),2),∴PM+PN=EH=eq \f(\r(2),2).
4.3eq \r(,2)
5.证明:延长CB到点H,使得HB=DF,连接AH.∵四边形ABCD是正方形,∴∠ABH=∠D=90°,AB=AD.∴△ADF绕点A顺时针旋转90°后能和△ABH重合,∴AH=AF,∠BAH=∠DAF.∵∠HAE=∠HAB+∠BAE=∠DAF+∠BAE=90°-∠EAF=90°-45°=45°,∴∠HAE=∠EAF=45°.又∵AE=AE,∴△AEF与△AEH关于直线AE对称,∴S△AEF=S△AEH=S△ABE+S△ABH=S△ABE+S△ADF.
6.证明:∵四边形ABCD是正方形,∴OB=OC,∠BOC=90°.将△OCP顺时针旋转90°至△OBE(如图所示),∴OE=OP,BE=CP,∠OBE=∠OCP,∠BOE=∠COP.∵BP⊥CP,∴∠BPC=90°.∵∠BOC+∠OBP+∠BPC+∠OCP=360°,∴∠OBP+∠OCP=180°,∴∠OBP+∠OBE=180°,∴E,B,P在同一直线上.∵∠POC+∠POB=∠BOC=90°,∠BOE=∠COP,∴∠BOE+∠POB=90°,即∠EOP=90°.在Rt△EOP中,由勾股定理得PE=eq \r(OE2+OP2)=eq \r(OP2+OP2)=eq \r(2)OP.∵PE=BE+BP,BE=CP,∴BP+CP=eq \r(2)OP.
相关试卷
这是一份中考训练解题技巧专题:特殊平行四边形中的解题方法专项训练与解析,共4页。试卷主要包含了利用对称性求最值【方法10】,利用面积法求定值等内容,欢迎下载使用。
这是一份沪科版数学八下 解题技巧专题:正方形中特殊的证明(计算)方法,共3页。试卷主要包含了3eq \r等内容,欢迎下载使用。
这是一份湘教版八下数学 解题技巧专题:勾股定理与面积问题,共3页。








