2021年广东省广州市天河区八年级（下）期末数学试卷（含答案）

这是一份2021年广东省广州市天河区八年级（下）期末数学试卷（含答案），共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2020-2021学年广东省广州市天河区八年级（下）期末数学试卷
一、选择题（本题有10个小题，每小题3分，满分30分，每小题给出的四个选项中，只有一个是正确的。）
1．（3分）式子在实数范围内有意义，则x的取值范围是（　　）
A．x≥0 B．x≤4 C．x≥﹣4 D．x≥4
2．（3分）下列选项中，属于最简二次根式的是（　　）
A． B． C． D．
3．（3分）一名射击爱好者5次射击的中靶环数如下：6，7，9，8，9．这5个数据的众数是（　　）
A．6 B．7 C．8 D．9
4．（3分）在△ABC中，D，E分别是AB，AC的中点，若BC＝10，AB＝12，则DE的长为（　　）
A．4 B．5 C．6 D．7
5．（3分）如图，每个小正方形的边长都是1，A，B，C分别在格点上，则∠ABC的度数为（　　）

A．30° B．45° C．50° D．60°
6．（3分）甲、乙、丙三人进行射箭测试，每人10次射箭成绩的平均数均是8.9环，方差分别是S甲2＝0.55，S乙2＝0.65，S丙2＝0.50，则成绩最稳定的是（　　）
A．甲 B．乙 C．丙 D．无法确定
7．（3分）小明向东走80m后，沿方向A又走了60m，再沿方向B走了100m回到原地，则方向A是（　　）
A．南向或北向 B．东向或西向 C．南向 D．北向
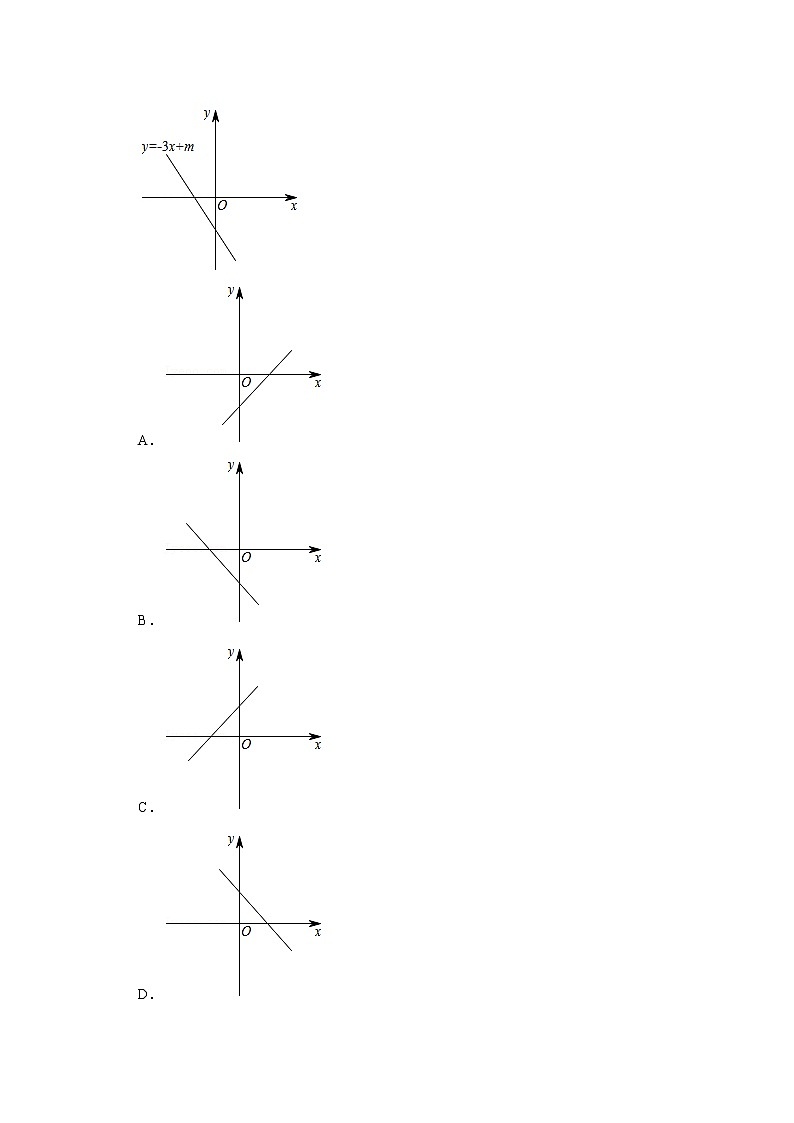
8．（3分）若函数y＝﹣3x+m的图象如图所示，则函数y＝mx+1的大致图象是（　　）

A．
B．
C．
D．
9．（3分）如图，将边长分别是4，8的矩形纸片ABCD折叠，使点C与点A重合，则BF的长是（　　）

A．2 B．3 C． D．4
10．（3分）已知矩形的对角线为1，面积为m，则矩形的周长为（　　）
A． B． C．2 D．2
二、填空题（本题有6个小题，每小题3分，共18分。）
11．（3分）在▱ABCD中，∠A＝50°，则∠C＝　 　°．
12．（3分）“若a＞0，b＞0，则ab＞0．”的逆命题为 　 　（填“真”或“假”）命题．
13．（3分）如图，在△ABC中，∠ABC＝90°，AD＝DC，BD＝4，则AC＝　 　．

14．（3分）如图，已知直线y1＝k1x+b1与直线y2＝k2x+b2相交于点A（1，2），若y1＜y2，则x的取值范围为 　 　．

15．（3分）一组数据4，2，x，6，3的平均数是4，则这组数据的中位数是 　 　．
16．（3分）观察3个式子：，，．猜想第四个式子得：＝　 　；依此类推，按照每个等式反映的规律，第n个二次根式的计算结果是 　 　．
三、解答题（本大题有8小题，共72分，解答要求写出文字说明，证明过程或计算步骤。）
17．（6分）计算：（）×．
18．（6分）在Rt△ABC中，∠C＝90°，∠A＝30°，AC＝3，求AB的长．
19．（8分）如图，在▱ABCD中，点E，F分别在AB，DC上，且AE＝CF．
求证：四边形DEBF是平行四边形．

20．（8分）某公司有15名员工，他们所在部门及相应每人所创年利润如表所示．
部门
人数
每人所创年利润/万元
A
5
3
B
2
8
C
1
7
D
4
4
E
3
9
（1）这个公司平均每人所创年利润是多少？
（2）公司规定，个人所创年利润由高到低前40%的人可以获奖．试判断D部门的员工能否获奖，并说明理由．
21．（10分）定义：有两个相邻内角互余的四边形称为邻余四边形，这两个角的夹边称为邻余线．
（1）如图1，在△ABC中，AB＝AC，AD是△ABC的中线，E，F分别是BD，AD上的点．求证：四边形ABEF是邻余四边形．
（2）如图2，在5×4的方格纸中，A，B在格点上，请画出一个符合条件的邻余四边形ABEF，使AB为邻余线，E，F在格点上．

22．（12分）A、B两家物流公司为了吸引顾客，推出不同的优惠方案，其中A公司原运费是5元/千克，现按8折计费．B公司原运费是6元/千克，优惠方案为：10千克以内不优惠，超过10千克部分按5折计费．
（1）以x（单位：千克）表示商品重量，y（单位：元）表示运费，分别就两家公司的优惠方案写出y关于x的函数解析式；
（2）在同一平面直角坐标系中画出（1）中两个函数的大致图象．
23．（10分）如图，直线y＝ax+6与直线y＝2x相交于点A（m，4），且与x轴相交于点B．
（1）求a和m值；
（2）求△AOB的边AB上的高．

24．（12分）已知在平面直角坐标系中，直线y＝2x﹣8与x轴交于点A，与y轴交于点B．
（1）求A，B的坐标；
（2）平移线段AB，使得点A，B的对应点M，N分别落在直线l1：y＝3x+6和直线l2：y＝x+4上，求M，N的坐标；
（3）试证明直线y＝kx+（1﹣k）恒平分四边形ABNM的面积，其中k≠0．

2020-2021学年广东省广州市天河区八年级（下）期末数学试卷
参考答案与试题解析
一、选择题（本题有10个小题，每小题3分，满分30分，每小题给出的四个选项中，只有一个是正确的。）
1．（3分）式子在实数范围内有意义，则x的取值范围是（　　）
A．x≥0 B．x≤4 C．x≥﹣4 D．x≥4
【解答】解：由题意得，x﹣4≥0，
解得，x≥4，
故选：D．
2．（3分）下列选项中，属于最简二次根式的是（　　）
A． B． C． D．
【解答】解：＝＝＝，∴B不符合题意；
＝＝4，∴C不符合题意；
＝＝，∴D不符合题意；
故选：A．
3．（3分）一名射击爱好者5次射击的中靶环数如下：6，7，9，8，9．这5个数据的众数是（　　）
A．6 B．7 C．8 D．9
【解答】解：∵9出现了2次，出现的次数最多，
∴这5个数据的众数是9；
故选：D．
4．（3分）在△ABC中，D，E分别是AB，AC的中点，若BC＝10，AB＝12，则DE的长为（　　）
A．4 B．5 C．6 D．7
【解答】解：∵D，E分别是AB，AC的中点，
∴DE为△ABC的中位线，
∴DE＝BC＝×10＝5．
故选：B．

5．（3分）如图，每个小正方形的边长都是1，A，B，C分别在格点上，则∠ABC的度数为（　　）

A．30° B．45° C．50° D．60°
【解答】解：如图，连AC，

则BC＝AC＝＝，AB＝＝，
∵（）2+（）2＝（）2，
即BC2+AC2＝AB2，
∴△ABC为等腰直角三角形，∠ACB＝90°，
∴∠ABC＝45°．
故选：B．
6．（3分）甲、乙、丙三人进行射箭测试，每人10次射箭成绩的平均数均是8.9环，方差分别是S甲2＝0.55，S乙2＝0.65，S丙2＝0.50，则成绩最稳定的是（　　）
A．甲 B．乙 C．丙 D．无法确定
【解答】解：∵S甲2＝0.55，S乙2＝0.65，S丙2＝0.50，
∴S丙2＜S甲2＜S乙2，
∴成绩最稳定的是丙，
故选：C．
7．（3分）小明向东走80m后，沿方向A又走了60m，再沿方向B走了100m回到原地，则方向A是（　　）
A．南向或北向 B．东向或西向 C．南向 D．北向
【解答】解：如图，
AB＝80m，AC＝AD＝60m，BC＝BD＝100m，
根据602+802＝1002得：∠BAC＝∠BAD＝90°，
故小明向东走80m后是向北或南方向走的．
故选：A．
8．（3分）若函数y＝﹣3x+m的图象如图所示，则函数y＝mx+1的大致图象是（　　）

A．
B．
C．
D．
【解答】解：由函数y＝﹣3x+m的图象可得：m＜0，
所以函数y＝mx+1的大致图象经过第一、二、四象限，
故选：D．
9．（3分）如图，将边长分别是4，8的矩形纸片ABCD折叠，使点C与点A重合，则BF的长是（　　）

A．2 B．3 C． D．4
【解答】解：由折叠的性质可知：AF＝CF．
设BF＝m，则AF＝CF＝8﹣m，
在Rt△ABF中，∠ABF＝90°，AB＝4，BF＝m，AF＝8﹣m，
∴AF2＝AB2+BF2，即（8﹣m）2＝42+m2，
∴m＝3．
故选：B．
10．（3分）已知矩形的对角线为1，面积为m，则矩形的周长为（　　）
A． B． C．2 D．2
【解答】解：设矩形的长、宽分别为a、b，
∵矩形的对角线为1，面积为m，
∴a²+b²＝1，ab＝m，
∴a+b＝＝＝，
∴矩形的周长为2（a+b）＝2，
故选：C．
二、填空题（本题有6个小题，每小题3分，共18分。）
11．（3分）在▱ABCD中，∠A＝50°，则∠C＝　50　°．
【解答】解：∵四边形ABCD是平行四边形，
∴∠C＝∠A＝50°．
故答案为：50．
12．（3分）“若a＞0，b＞0，则ab＞0．”的逆命题为 　假　（填“真”或“假”）命题．
【解答】解：“若a＞0，b＞0，则ab＞0”的逆命题是“若ab＞0，则a＞0，b＞0”，是一个假命题，
故答案为：假．
13．（3分）如图，在△ABC中，∠ABC＝90°，AD＝DC，BD＝4，则AC＝　8　．

【解答】解：∵AD＝DC，
∴D为AC边上的中点，
在△ABC中，∠ABC＝90°，BD＝4，
∴AC＝2BD＝8．
故答案为8．
14．（3分）如图，已知直线y1＝k1x+b1与直线y2＝k2x+b2相交于点A（1，2），若y1＜y2，则x的取值范围为 　x＜1　．

【解答】解：如图，已知直线y1＝k1x+b1与直线y2＝k2x+b2相交于点A（1，2），则当y1＜y2时，x的取值范围为 x＜1．
故答案是：x＜1．

15．（3分）一组数据4，2，x，6，3的平均数是4，则这组数据的中位数是 　4　．
【解答】解：由题意得，＝4，
解得x＝5，
将4，2，5，6，3从小到大排列为2，3，4，5，6，处在中间位置的一个数是4，因此中位数是4，
故答案为：4．
16．（3分）观察3个式子：，，．猜想第四个式子得：＝　1　；依此类推，按照每个等式反映的规律，第n个二次根式的计算结果是 　　．
【解答】解：猜想第四个式子得：＝1+﹣＝1；
第n个二次根式的计算结果为1+﹣＝＝．
故答案为1；．
三、解答题（本大题有8小题，共72分，解答要求写出文字说明，证明过程或计算步骤。）
17．（6分）计算：（）×．
【解答】解：原式＝（2+2）×
＝2+2
＝4+6．
18．（6分）在Rt△ABC中，∠C＝90°，∠A＝30°，AC＝3，求AB的长．
【解答】解：如图所示，在Rt△ABC中，∠C＝90°，∠A＝30°，

∴BC＝AB，
∵AC＝3，AB2＝BC2+AC2＝（AB）2+32，
解得AB＝．
19．（8分）如图，在▱ABCD中，点E，F分别在AB，DC上，且AE＝CF．
求证：四边形DEBF是平行四边形．

【解答】证明：∵四边形ABCD是平行四边形，
∴AB＝CD，AB∥CD，
∵AE＝CF，
∴AB﹣AE＝CD﹣CF，
即BE＝DF，
∵DF∥BE
∴四边形DEBF是平行四边形．
20．（8分）某公司有15名员工，他们所在部门及相应每人所创年利润如表所示．
部门
人数
每人所创年利润/万元
A
5
3
B
2
8
C
1
7
D
4
4
E
3
9
（1）这个公司平均每人所创年利润是多少？
（2）公司规定，个人所创年利润由高到低前40%的人可以获奖．试判断D部门的员工能否获奖，并说明理由．
【解答】解：（1）根据题意得：
×（5×3+2×8+1×7+4×4+3×9）＝5.4（万元），
答：这个公司平均每人所创年利润是5.4万元．

（2）D部门的员工不能获奖，理由如下：
获奖人数为：15×40%＝6（人），
个人所创年利润由高到低分别为E部门3人，B部门2人，C部门1人，工6人，所以D部门的员工不能获奖．
21．（10分）定义：有两个相邻内角互余的四边形称为邻余四边形，这两个角的夹边称为邻余线．
（1）如图1，在△ABC中，AB＝AC，AD是△ABC的中线，E，F分别是BD，AD上的点．求证：四边形ABEF是邻余四边形．
（2）如图2，在5×4的方格纸中，A，B在格点上，请画出一个符合条件的邻余四边形ABEF，使AB为邻余线，E，F在格点上．

【解答】（1）证明：∵AB＝AC，AD是△ABC的中线，
∴AD⊥BC，
∴∠ADB＝90°，
∴∠FAB+∠B＝90°，
∴四边形ABEF是邻余四边形；

（2）解：如图2所示，即为所求．（答案不唯一，正确即可）．

22．（12分）A、B两家物流公司为了吸引顾客，推出不同的优惠方案，其中A公司原运费是5元/千克，现按8折计费．B公司原运费是6元/千克，优惠方案为：10千克以内不优惠，超过10千克部分按5折计费．
（1）以x（单位：千克）表示商品重量，y（单位：元）表示运费，分别就两家公司的优惠方案写出y关于x的函数解析式；
（2）在同一平面直角坐标系中画出（1）中两个函数的大致图象．
【解答】解：（1）A公司：y＝4x（x≥0），
B公司：y＝；
（2）如图所示：

23．（10分）如图，直线y＝ax+6与直线y＝2x相交于点A（m，4），且与x轴相交于点B．
（1）求a和m值；
（2）求△AOB的边AB上的高．

【解答】解：（1）∵函数y＝2x的图象过点A（m，4），
∴4＝2m，解得m＝2，
∴A点坐标为（2，4）．
∵y＝ax+6的图象过点A，
∴2a+6＝4，解得a＝﹣1；

（2）把a＝﹣1代入y＝ax+6得y＝﹣x+6，
∴y＝0时，﹣x+6＝0．解得x＝6，
∴B（6，0），OB＝6，
过A作AC⊥OB于C，
∵A（2，4），
∴AC＝4，OC＝2，CB＝4，
在Rt△ACB中，AB＝＝4，
设△AOB的边AB上的高为h，
∴S△AOB＝OB•AC＝AB•h＝×6×4＝12；
∴×4•h＝12，
∴h＝3，
即△AOB的边AB上的高为3．

24．（12分）已知在平面直角坐标系中，直线y＝2x﹣8与x轴交于点A，与y轴交于点B．
（1）求A，B的坐标；
（2）平移线段AB，使得点A，B的对应点M，N分别落在直线l1：y＝3x+6和直线l2：y＝x+4上，求M，N的坐标；
（3）试证明直线y＝kx+（1﹣k）恒平分四边形ABNM的面积，其中k≠0．
【解答】解：（1）在直线y＝2x﹣8中，
令y＝0，则2x﹣8＝0，
∴x＝4，
∴A（4，0），
令x＝0，则y＝﹣8，
∴B（0，﹣8）；

（2）由（1）知，A（4，0），B（0，﹣8），
当点N在直线l2：y＝x+4上时，设N（t，t+4），
∵线段MN是由相等AB平移得到，
由点B（0，﹣8）移动到点N（t，t+4），
即点B向右移动t个单位，再向上平移t+4+8个单位，
∴点A也向右移动t个单位，再向上平移t+4+8个单位，
∴点A（4，0）相应移动到点M（t+4，t+4+8），
即点M（t+4，t+12），
∵点M在直线l1：y＝3x+6上，
∴3（t+4）+6＝t+12，
∴t＝﹣3，
∴M（1，9），N（﹣3，1）；

（3）∵线段AB平移得到线段MN，
∴AB∥MN，AB＝MN，
∴四边形ABNM是平行四边形，
连接对角线AN，BM相交于点C，
∴AN，BM互相平分，
即点C是AN的中点，
∵A（4，0），N（﹣3，1），
∴C（，），
即C（，），
∵直线y＝kx+（1﹣k）＝kx﹣k+＝k（x﹣）+，
∴直线y＝kx+（1﹣k）恒过点（，），此点是平行四边形的对角线的交点，
即直线y＝kx+（1﹣k）恒平分四边形ABNM的面积，其中k≠0．

声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布
日期：2022/2/21 13:38:26；用户：校园号；邮箱：gx998@xyh.com；学号：40932698