2021年江西省吉安市峡江县八年级（下）期末数学试卷+答案

这是一份2021年江西省吉安市峡江县八年级（下）期末数学试卷+答案，共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2020-2021学年江西省吉安市峡江县八年级（下）期末数学试卷
一、选择题（本大题共6小题，每小题只有一个正确答案，每小题3分，共18分）
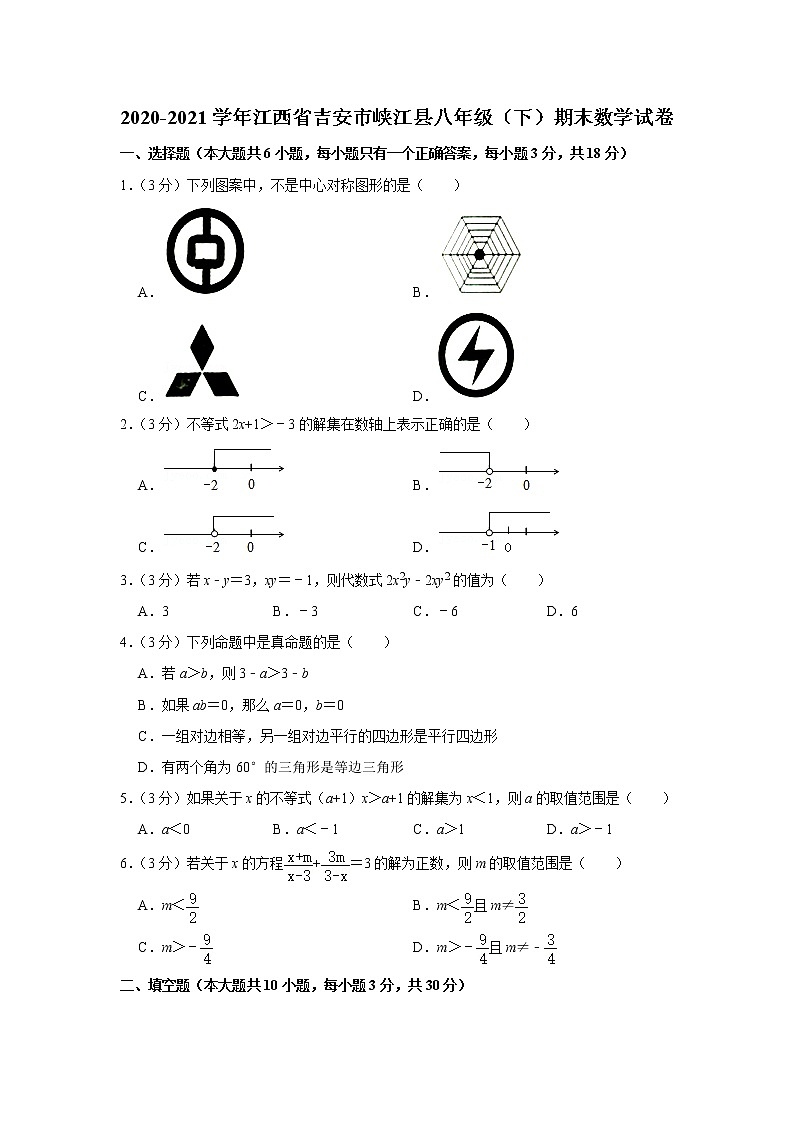
1．（3分）下列图案中，不是中心对称图形的是（　　）
A． B．
C． D．
2．（3分）不等式2x+1＞﹣3的解集在数轴上表示正确的是（　　）
A． B．
C． D．
3．（3分）若x﹣y＝3，xy＝﹣1，则代数式2x2y﹣2xy2的值为（　　）
A．3 B．﹣3 C．﹣6 D．6
4．（3分）下列命题中是真命题的是（　　）
A．若a＞b，则3﹣a＞3﹣b
B．如果ab＝0，那么a＝0，b＝0
C．一组对边相等，另一组对边平行的四边形是平行四边形
D．有两个角为60°的三角形是等边三角形
5．（3分）如果关于x的不等式（a+1）x＞a+1的解集为x＜1，则a的取值范围是（　　）
A．a＜0 B．a＜﹣1 C．a＞1 D．a＞﹣1
6．（3分）若关于x的方程+＝3的解为正数，则m的取值范围是（　　）
A．m＜ B．m＜且m≠
C．m＞﹣ D．m＞﹣且m≠﹣
二、填空题（本大题共10小题，每小题3分，共30分）
7．（3分）若分式的值为0，则x等于 　 　．
8．（3分）一个多边形的每一个内角为108°，则这个多边形是　 　边形．
9．（3分）如图，在Rt△ABC中，∠ACB＝90°，AC＝8，AB＝10，DE是△ABC的中位线，则
DE＝　 　．

10．（3分）若关于x的方程＝有增根，则m的值是 　 　．
11．（3分）如图，△ABC中，EF是AB的垂直平分线，与AB交于点D，BF＝10，CF＝2，则AC＝　 　．

12．（3分）如图，在△ABC中，AB＝4，BC＝6，∠B＝60°，将△ABC沿射线BC方向平移2个单位后得到△DEF，连接DC，则DC的长为　 　．

13．（3分）小马用100元钱去购买笔记本和钢笔共30件，已知每本笔记本2元，每支钢笔5元，那么小马最多能买支　 　钢笔．
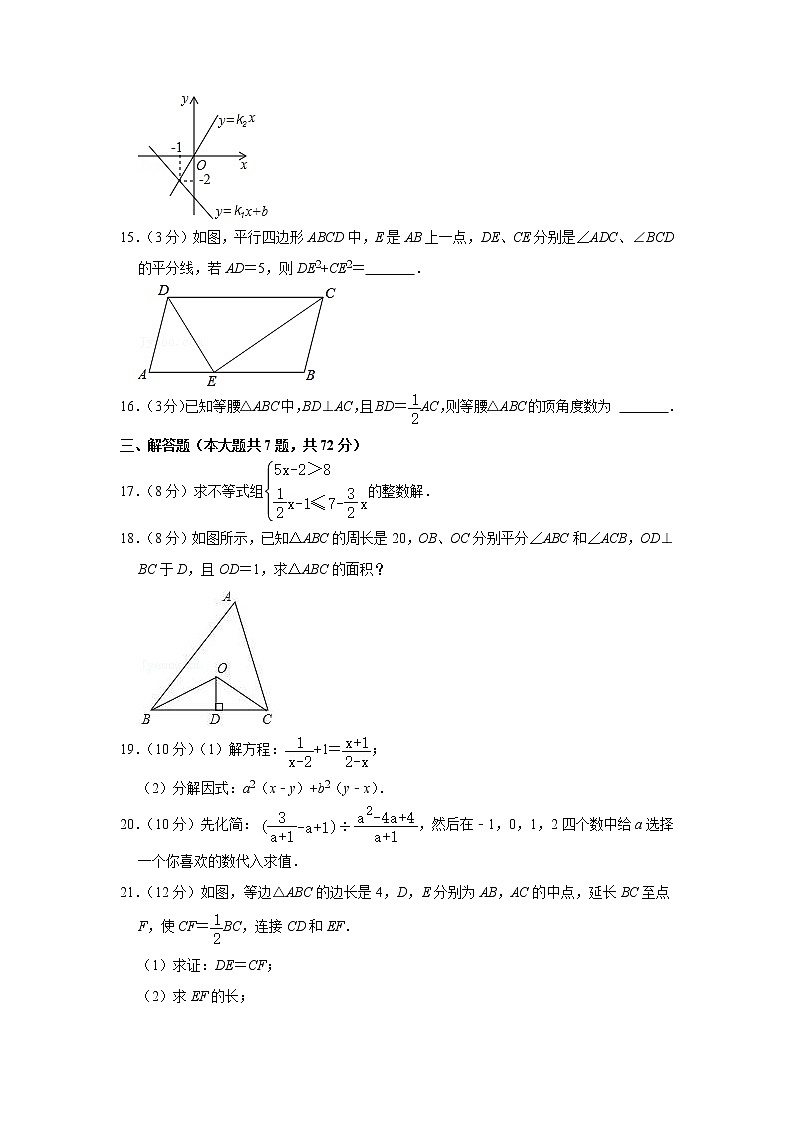
14．（3分）直线l1：y＝k1x+b与直线l2：y＝k2x在同一平面直角坐标系中的图象如图所示，则关于x的不等式k1x+b＞k2x的解集为　 　．

15．（3分）如图，平行四边形ABCD中，E是AB上一点，DE、CE分别是∠ADC、∠BCD的平分线，若AD＝5，则DE2+CE2＝　 　．

16．（3分）已知等腰△ABC中，BD⊥AC，且BD＝AC，则等腰△ABC的顶角度数为 　 　．
三、解答题（本大题共7题，共72分）
17．（8分）求不等式组的整数解．
18．（8分）如图所示，已知△ABC的周长是20，OB、OC分别平分∠ABC和∠ACB，OD⊥BC于D，且OD＝1，求△ABC的面积？

19．（10分）（1）解方程：+1＝；
（2）分解因式：a2（x﹣y）+b2（y﹣x）．
20．（10分）先化简：，然后在﹣1，0，1，2四个数中给a选择一个你喜欢的数代入求值．
21．（12分）如图，等边△ABC的边长是4，D，E分别为AB，AC的中点，延长BC至点F，使CF＝BC，连接CD和EF．
（1）求证：DE＝CF；
（2）求EF的长；
（3）求四边形DEFC的面积．

22．（12分）某学校在商场购买甲、乙两种不同足球，购买甲种足球共花费2000元，购买乙种足球共花费1400元，购买甲种足球数量是购买乙种足球数量的2倍，且购买一个乙种足球比购买一个甲种足球多花20元．
（1）求购买一个甲种足球、一个乙种足球各需多少元？
（2）为响应“足球进校园”的号召，这所学校决定再次购买甲、乙两种足球共50个．恰逢该商场对两种足球的售价进行调整，甲种足球售价比第一次购买时提高了10%，乙种足球售价比第一次购买时降低了10%，如果此次购买甲、乙两种足球的总费用不超过2900元，那么这所学校最多可购买多少个乙种足球？
23．（12分）作图题
如图，在平面直角坐标系中，有一Rt△ABC，且A（﹣1，3），B（﹣3，﹣1），C（﹣3，3），已知△A1AC1是由△ABC旋转得到的．
（1）请写出旋转中心的坐标是　 　，旋转角是　 　度；
（2）设线段AB所在直线AB表达式为y＝kx+b，试求出当y＞2时，x的取值范围是　 　；
（3）点Q在x轴上，点P在直线AB上，要使以Q、P、A1、C1为顶点的四边形是平行四边形，直接写出满足条件点P的坐标（只要写出一个解）．


2020-2021学年江西省吉安市峡江县八年级（下）期末数学试卷
参考答案与试题解析
一、选择题（本大题共6小题，每小题只有一个正确答案，每小题3分，共18分）
1．（3分）下列图案中，不是中心对称图形的是（　　）
A． B．
C． D．
【解答】解：A、是中心对称图形，故本选项错误；
B、是中心对称图形，故本选项错误；
C、不是中心对称图形，故本选项正确；
D、是中心对称图形，故本选项错误．
故选：C．
2．（3分）不等式2x+1＞﹣3的解集在数轴上表示正确的是（　　）
A． B．
C． D．
【解答】解：不等式2x+1＞﹣3，
移项，得2x＞﹣1﹣3，
合并，得2x＞﹣4，
化系数为1，得x＞﹣2．
故选：C．
3．（3分）若x﹣y＝3，xy＝﹣1，则代数式2x2y﹣2xy2的值为（　　）
A．3 B．﹣3 C．﹣6 D．6
【解答】解：2x2y﹣2xy2＝2xy（x﹣y）
当x﹣y＝3，xy＝﹣1时，
原式＝2×（﹣1）×3＝﹣6．
故选：C．
4．（3分）下列命题中是真命题的是（　　）
A．若a＞b，则3﹣a＞3﹣b
B．如果ab＝0，那么a＝0，b＝0
C．一组对边相等，另一组对边平行的四边形是平行四边形
D．有两个角为60°的三角形是等边三角形
【解答】解：A、若a＞b，则3﹣a＜3﹣b，是假命题；
B、如果ab＝0，那么a＝0或b＝0或a＝0，b＝0，是假命题；
C、一组对边相等且平行的四边形是平行四边形，是假命题；
D、有两个角为60°的三角形是等边三角形，是真命题；
故选：D．
5．（3分）如果关于x的不等式（a+1）x＞a+1的解集为x＜1，则a的取值范围是（　　）
A．a＜0 B．a＜﹣1 C．a＞1 D．a＞﹣1
【解答】解：由题意，得
a+1＜0，
解得a＜﹣1，
故选：B．
6．（3分）若关于x的方程+＝3的解为正数，则m的取值范围是（　　）
A．m＜ B．m＜且m≠
C．m＞﹣ D．m＞﹣且m≠﹣
【解答】解：去分母得：x+m﹣3m＝3x﹣9，
整理得：2x＝﹣2m+9，
解得：x＝，
∵关于x的方程+＝3的解为正数，
∴﹣2m+9＞0且≠3
解得：m＜且m≠，
故m的取值范围是：m＜且m≠．
故选：B．
二、填空题（本大题共10小题，每小题3分，共30分）
7．（3分）若分式的值为0，则x等于 　﹣2　．
【解答】解：分式的值为0，则，
解得x＝﹣2，
故答案为：﹣2．
8．（3分）一个多边形的每一个内角为108°，则这个多边形是　五　边形．
【解答】解：∵多边形每个内角都为108°，
∴多边形每个外角都为180°﹣108°＝72°，
∴边数＝360°÷72°＝5．
故答案为：五．
9．（3分）如图，在Rt△ABC中，∠ACB＝90°，AC＝8，AB＝10，DE是△ABC的中位线，则
DE＝　3　．

【解答】解：∵∠ACB＝90°，AC＝8，AB＝10，
∴BC＝＝6，
∵DE是△ABC的中位线，
∴DE＝BC＝3，
故答案为：3．
10．（3分）若关于x的方程＝有增根，则m的值是 　3　．
【解答】解：方程两边都乘（x﹣2），得x+1＝m
∵方程有增根，
∴增根使最简公分母x﹣2＝0，即增根是x＝2，
把x＝2代入整式方程，得m＝3．
故答案为3．
11．（3分）如图，△ABC中，EF是AB的垂直平分线，与AB交于点D，BF＝10，CF＝2，则AC＝　12　．

【解答】解：∵EF是AB的垂直平分线，
∴FA＝BF＝10，
∴AC＝AF+FC＝12．
故答案为：12．
12．（3分）如图，在△ABC中，AB＝4，BC＝6，∠B＝60°，将△ABC沿射线BC方向平移2个单位后得到△DEF，连接DC，则DC的长为　4　．

【解答】解：∵△ABC沿射线BC方向平移2个单位后得到△DEF，
∴DE＝AB＝4，BC﹣BE＝6﹣2＝4，
∵∠B＝∠DEC＝60°，
∴△DEC是等边三角形，
∴DC＝4，
故答案为：4．
13．（3分）小马用100元钱去购买笔记本和钢笔共30件，已知每本笔记本2元，每支钢笔5元，那么小马最多能买支　13　钢笔．
【解答】解：设小马能买x支钢笔，则可购买（30﹣x）本笔记本．
2（30﹣x）+5x≤100，
解得，x≤，
∵购买的钢笔为整数，
∴最多购买钢笔13支，
故答案为：13．
14．（3分）直线l1：y＝k1x+b与直线l2：y＝k2x在同一平面直角坐标系中的图象如图所示，则关于x的不等式k1x+b＞k2x的解集为　x＜﹣1　．

【解答】能使函数y＝k1x+b的图象在函数y＝k2x的上边时的自变量的取值范围是x＜﹣1．
故关于x的不等式k1x+b＞k2x的解集为：x＜﹣1．
故答案为：x＜﹣1．
15．（3分）如图，平行四边形ABCD中，E是AB上一点，DE、CE分别是∠ADC、∠BCD的平分线，若AD＝5，则DE2+CE2＝　100　．

【解答】解：∵DE、CE分别是∠ADC、∠BCD的平分线，
∴∠ADE＝∠CDE，∠DCE＝∠BCE，
∵四边形ABCD是平行四边形，
∴AB∥DC，AD＝BC＝5，∠ADC+∠BCD＝180°，
∴∠CDE＝∠DEA，∠DCE＝∠CEB，
∴∠ADE＝∠AED，∠BCE＝∠BEC，∠EDC+∠ECD＝90°，
∴DA＝AE＝5，BC＝BE＝5，∠DEC＝90°，
∴AB＝CD＝10，
∴DE2+CE2＝CD2＝102＝100，
故答案为：100．
16．（3分）已知等腰△ABC中，BD⊥AC，且BD＝AC，则等腰△ABC的顶角度数为 　90°或30°或150°　．
【解答】解：如图1中，当AB＝AC时，

∵BD⊥AC，BD＝AC，
∴AB＝2BD，
∴∠A＝30°，
如图2中，当AB＝AC，

∵BD⊥AC，BD＝AC，
∴AB＝2BD，
∴∠DAB＝30°，
∴∠BAC＝150°，

如图3中，当BA＝BC，

∵BD⊥AC，BA＝BC，
∴BD＝AD＝DC，
∴∠A＝∠ABD＝∠CBD＝∠C＝45°，
∴∠ABC＝90°，
综上所述，满足条件的等腰三角形的顶角的度数为30°或150°或90°．
故答案为：30°或150°或90°．
三、解答题（本大题共7题，共72分）
17．（8分）求不等式组的整数解．
【解答】解：
由①得：x＞2；
由②得：x≤4，
∴2＜x≤4
∴不等式组的整数解为3，4．
18．（8分）如图所示，已知△ABC的周长是20，OB、OC分别平分∠ABC和∠ACB，OD⊥BC于D，且OD＝1，求△ABC的面积？

【解答】解：如图，连接OA，过O作OE⊥AB于E，OF⊥AC于F，
∵OB、OC分别平分∠ABC和∠ACB，
∴OE＝OF＝OD＝1，
∵△ABC的周长是20，OD⊥BC于D，且OD＝1，
∴S△ABC＝×AB×OE+×BC×OD+×AC×OF＝×（AB+BC+AC）×1
＝×20×1＝10，

19．（10分）（1）解方程：+1＝；
（2）分解因式：a2（x﹣y）+b2（y﹣x）．
【解答】解：（1）去分母得：1+x﹣2＝﹣x﹣1，
解得：x＝0，
检验：把x＝0代入：x﹣2＝﹣2≠0，
∴原方程的解为x＝0；
（2）原式＝a2（x﹣y）﹣b2（x﹣y）
＝（x﹣y）（a2﹣b2）
＝（x﹣y）（a﹣b）（a+b）．
20．（10分）先化简：，然后在﹣1，0，1，2四个数中给a选择一个你喜欢的数代入求值．
【解答】解：原式＝•
＝•
＝•
＝
＝，
∵要使分式有意义，故a+1≠0且a﹣2≠0，
∴a≠﹣1且a≠2，
∴a＝1时，原式＝＝3．
21．（12分）如图，等边△ABC的边长是4，D，E分别为AB，AC的中点，延长BC至点F，使CF＝BC，连接CD和EF．
（1）求证：DE＝CF；
（2）求EF的长；
（3）求四边形DEFC的面积．

【解答】解：（1）在△ABC中，
∵D、E分别为AB、AC的中点，
∴DE为△ABC的中位线，
∴DE＝BC，
∵CF＝BC，
∴DE＝CF．

（2）∵AC＝BC，AD＝BD，
∴CD⊥AB，
∵BC＝4，BD＝2，
∴CD＝＝2，
∵DE∥CF，DE＝CF，
∴四边形DEFC是平行四边形，
∴EF＝CD＝2．

（3）过点D作DH⊥BC于H．

∵∠DHC＝90°，∠DCB＝30°，
∴DH＝DC＝，
∵DE＝CF＝2，
∴S四边形DEFC＝CF•DH＝2×＝2．
22．（12分）某学校在商场购买甲、乙两种不同足球，购买甲种足球共花费2000元，购买乙种足球共花费1400元，购买甲种足球数量是购买乙种足球数量的2倍，且购买一个乙种足球比购买一个甲种足球多花20元．
（1）求购买一个甲种足球、一个乙种足球各需多少元？
（2）为响应“足球进校园”的号召，这所学校决定再次购买甲、乙两种足球共50个．恰逢该商场对两种足球的售价进行调整，甲种足球售价比第一次购买时提高了10%，乙种足球售价比第一次购买时降低了10%，如果此次购买甲、乙两种足球的总费用不超过2900元，那么这所学校最多可购买多少个乙种足球？
【解答】解：（1）设购买一个甲种足球需x元，则购买一个乙种足球需（x+20）元，
根据题意，可得：＝2×，
解得：x＝50，
经检验x＝50是原方程的解，
答：购买一个甲种足球需50元，购买一个乙种足球需70元；

（2）设这所学校再次购买y个乙种足球，
根据题意，可得：50×（1+10%）×（50﹣y）+70×（1﹣10%）y≤2900，
解得：y≤18.75，
由题意可得，最多可购买18个乙种足球，
答：这所学校最多可购买18个乙种足球．
23．（12分）作图题
如图，在平面直角坐标系中，有一Rt△ABC，且A（﹣1，3），B（﹣3，﹣1），C（﹣3，3），已知△A1AC1是由△ABC旋转得到的．
（1）请写出旋转中心的坐标是　（0，0）　，旋转角是　90　度；
（2）设线段AB所在直线AB表达式为y＝kx+b，试求出当y＞2时，x的取值范围是　x＞﹣　；
（3）点Q在x轴上，点P在直线AB上，要使以Q、P、A1、C1为顶点的四边形是平行四边形，直接写出满足条件点P的坐标（只要写出一个解）．

【解答】解：（1）旋转中心的坐标是（0，0），旋转角是90度；
故答案为（0，0），90．

（2）∵由图可知A（﹣1，3），B（﹣3，﹣1），
∴设直线AB的解析式为y＝kx+b（k≠0），则
，
解得，
∴直线AB的解析式为：y＝2x+5；
∵y＞2，
∴2x+5＞2，
解得：x＞﹣，
∴当x＞﹣时，y＞2．

（3）∵点Q在x轴上，点P在直线AB上，以Q、P、A1、C1为顶点的四边形是平行四边形，
①当A1C1为平行四边形的边时，
∴PQ＝A1C1＝2，
∵P点在直线y＝2x+5上，
∴令y＝2时，2x+5＝2，解得x＝﹣，
令y＝﹣2时，2x+5＝﹣2，解得x＝﹣，
②当A1C1为平行四边形的对角线时，
∵A1C1的中点坐标为（3，2），
∴P的纵坐标为4，
代入y＝2x+5得，4＝2x+5，
解得x＝﹣，
∴P（﹣，4），
故P为（﹣，2）或（﹣，﹣2）或（﹣，4）．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布
日期：2022/2/21 14:21:29；用户：校园号；邮箱：gx998@xyh.com；学号：40932698