2021年四川省巴中市七年级下学期期末考试数学试题+答案

这是一份2021年四川省巴中市七年级下学期期末考试数学试题+答案，共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2020-2021学年四川省巴中市七年级（下）期末数学试卷
一、选择题（本大题12个小题，每小题4分，共48分）
1．方程2a＝﹣4的解是（　　）
A．a＝2 B．a＝﹣2 C．a＝﹣ D．a＝﹣6
2．以下四个标志中，是轴对称图形的是（　　）
A． B． C． D．
3．根据不等式的性质，下列变形正确的是（　　）
A．由a＞b得ac2＞bc2 B．由ac2＞bc2得a＞b
C．由﹣a＞2得a＜2 D．由2x+1＞x得x＞1
4．人字梯中间一般会设计一“拉杆”，这样做的道理是（　　）

A．两点之间，线段最短
B．垂线段最短
C．两直线平行，内错角相等
D．三角形具有稳定性
5．如图所示，一个正方形水池的四周恰好被4个正n边形地板砖铺满，则n等于（　　）

A．4 B．6 C．8 D．10
6．二元一次方程2x+3y＝11的正整数解有（　　）
A．2组 B．3组 C．4组 D．5组
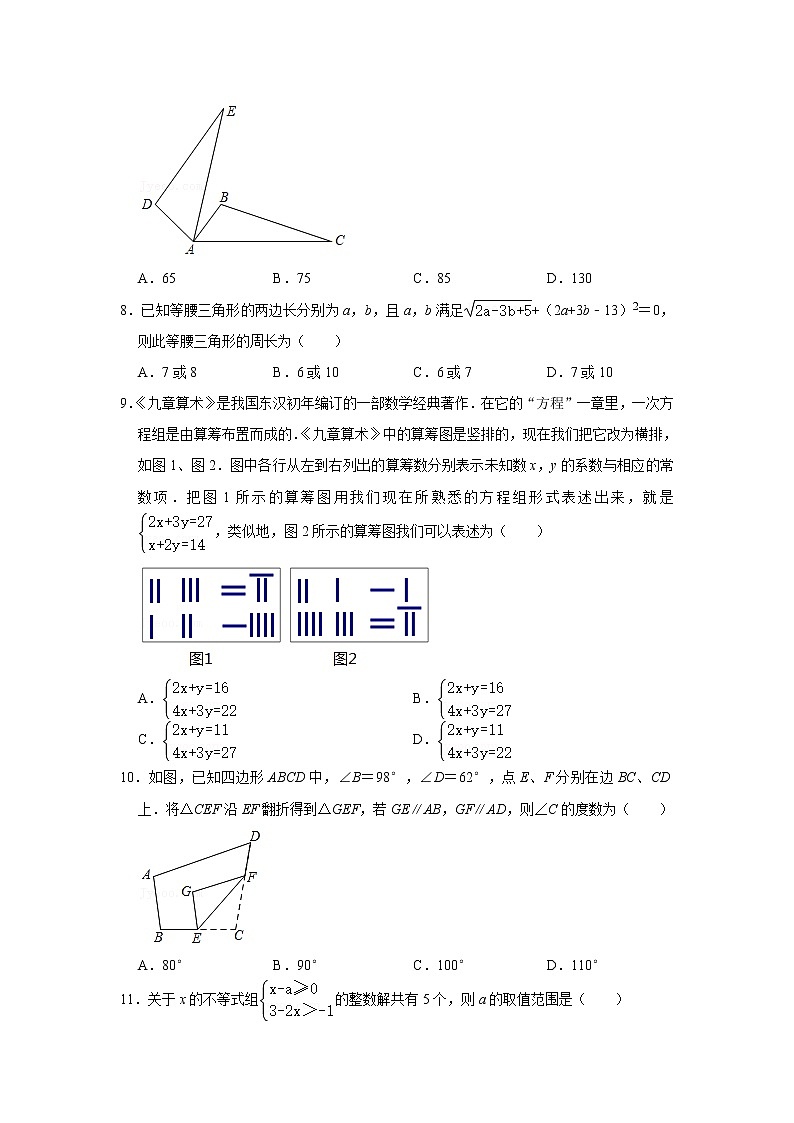
7．如图，在△ABC中，∠BAC＝65°，∠C＝20°，将△ABC绕点A逆时针旋转n度（0＜n＜180）得到△ADE，若DE∥AB，则n的值为（　　）

A．65 B．75 C．85 D．130
8．已知等腰三角形的两边长分别为a，b，且a，b满足+（2a+3b﹣13）2＝0，则此等腰三角形的周长为（　　）
A．7或8 B．6或10 C．6或7 D．7或10
9．《九章算术》是我国东汉初年编订的一部数学经典著作．在它的“方程”一章里，一次方程组是由算筹布置而成的．《九章算术》中的算筹图是竖排的，现在我们把它改为横排，如图1、图2．图中各行从左到右列出的算筹数分别表示未知数x，y的系数与相应的常数项．把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来，就是，类似地，图2所示的算筹图我们可以表述为（　　）

A． B．
C． D．
10．如图，已知四边形ABCD中，∠B＝98°，∠D＝62°，点E、F分别在边BC、CD上．将△CEF沿EF翻折得到△GEF，若GE∥AB，GF∥AD，则∠C的度数为（　　）

A．80° B．90° C．100° D．110°
11．关于x的不等式组的整数解共有5个，则a的取值范围是（　　）
A．a＝﹣3 B．﹣4＜a＜﹣3 C．﹣4≤a＜﹣3 D．﹣4＜a≤﹣3
12．在直角三角形ABC中，∠C＝90°，AD平分∠BAC交BC于点D，BE平分∠ABC交AC于点E，AD、BE相交于点F，过点D作DG∥AB，过点B作BG⊥DG交DG于点G．下列结论：①∠AFB＝135°；②∠BDG＝2∠CBE；③BC平分∠ABG；④∠BEC＝∠FBG．其中正确的个数是（　　）

A．1个 B．2个 C．3个 D．4个
二、填空题（本大题6个小题，每小题3分，共18分）
13．（3分）若一个正多边形的一个内角等于140°，那么这个多边形是正　 　边形．
14．（3分）如图，已知△ABC≌△ADE，若AB＝7，AC＝3，则BE的值为　 　．

15．（3分）若关于x的方程（k﹣2）x|k﹣1|+5k+1＝0是一元一次方程，则k＝　 　．
16．（3分）若不等式组的解集为2＜x＜3，则（a+b）2021＝　 　．
17．（3分）按下面的程序计算，若开始输入的x值为正数，最后输出的结果为53，请写出符合条件的所有x的值 　 　．

18．（3分）如图，长方形ABCD中，AB＝4，AD＝2．点Q与点P同时从点A出发，点Q以每秒1个单位的速度沿A→D→C→B的方向运动，点P以每秒3个单位的速度沿A→B→C→D的方向运动，当P，Q两点相遇时，它们同时停止运动．设Q点运动的时间为x（秒），在整个运动过程中，当△APQ为直角三角形时，则相应的x的值或取值范围是　 　．

三、解答题（本大题8个小题，共84分）
19．（10分）（1）解方程：2+5x＝8+3x．
（2）解不等式组，并把解集在数轴上表示出来．
20．（8分）甲、乙两位同学在解关于x、y的方程组时，甲同学看错a得到方程的解为，乙同学看错b得到方程组的，求x+y的值．
21．（10分）如图所示的正方形网格中，每个小正方形的边长均为1个单位，△ABC的三个顶点都在格点上．
（1）在网格中画出△ABC向下平移3个单位得到的△A1B1C1；
（2）在网格中画出△ABC关于直线m对称的△A2B2C2；
（3）在直线m上画一点P，使得C1P+C2P的值最小．

22．（10分）已知关于x、y的方程组中，x为非负数、y为负数．
（1）试求m的取值范围；
（2）当m取何整数时，不等式3mx+2x＞3m+2的解集为x＜1．
23．（10分）如图，在△ABC中，CM⊥AB于点M，∠ACB的平分线CN交AB于点N，过点N作ND∥AC交BC点D．若∠A＝78°，∠B＝50°．求：
（1）∠CND的度数；
（2）∠MCN的度数．

24．（10分）某中学计划购买A型和B型课桌凳共200套．经招标，购买一套A型课桌凳比购买一套B型课桌凳少用40元，且购买4套A型和5套B型课桌凳共需1820元．
（1）求购买一套A型课桌凳和一套B型课桌凳各需多少元？
（2）学校根据实际情况，要求购买这两种课桌凳总费用不能超过40880元，并且购买A型课桌凳的数量不能超过B型课桌凳数量的，求该校本次购买A型和B型课桌凳共有几种方案？哪种方案的总费用最低？
25．（12分）定义：对于任何有理数m，符号【m】表示不大于m的最大整数．例如：【4.5】＝4，【8】＝8，【﹣3.2】＝﹣4．
（1）填空：【π】＝　 　，【﹣2.1】+【5.1】＝　 　．
（2）求方程4x﹣3【x】+5＝0的整数解；
（3）如果【】＝﹣4，求满足条件的x的取值范围．
26．（14分）如图1，点D为△ABC边BC的延长线上一点．
（1）若∠A：∠ABC＝3：4，∠ACD＝140°，求∠A的度数；
（2）若∠ABC的角平分线与∠ACD的角平分线交于点M，过点C作CP⊥BM于点P．求证：∠MCP＝90°﹣∠A；
（3）在（2）的条件下，将△MBC以直线BC为对称轴翻折得到△NBC，∠NBC的角平分线与∠NCB的角平分线交于点Q（如图2），试探究∠BQC与∠A有怎样的数量关系，请写出你的猜想并证明．


2020-2021学年四川省巴中市七年级（下）期末数学试卷
参考答案与试题解析
一、选择题（本大题12个小题，每小题4分，共48分）
1．方程2a＝﹣4的解是（　　）
A．a＝2 B．a＝﹣2 C．a＝﹣ D．a＝﹣6
【分析】根据等式的性质，把方程的系数化为1即可．
【解答】解：2a＝﹣4，
方程两边同时除以2，得a＝﹣2．
故选：B．
2．以下四个标志中，是轴对称图形的是（　　）
A． B． C． D．
【分析】如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，利用轴对称图形的定义进行解答即可．
【解答】解：选项B，C，D不能找到这样的一条直线，使这个图形沿一条直线折叠，直线两旁的部分能够互相重合，所以这些图形不是轴对称图形；
选项A能找到这样的一条直线，使这个图形沿一条直线折叠，直线两旁的部分能够互相重合，所以这个图形是轴对称图形；
故选：A．
3．根据不等式的性质，下列变形正确的是（　　）
A．由a＞b得ac2＞bc2 B．由ac2＞bc2得a＞b
C．由﹣a＞2得a＜2 D．由2x+1＞x得x＞1
【分析】根据不等式的性质，可得答案．
【解答】解；A、a＞b，c＝0时，ac2＝bc2，故A不符合题意；
B、由ac2＞bc2得a＞b，故B符合题意；
C、由﹣a＞2得a＜﹣4，故C不符合题意；
D、由2x+1＞x得x＞﹣1，故D不符合题意；
故选：B．
4．人字梯中间一般会设计一“拉杆”，这样做的道理是（　　）

A．两点之间，线段最短
B．垂线段最短
C．两直线平行，内错角相等
D．三角形具有稳定性
【分析】根据三角形的稳定性解答即可．
【解答】解：人字梯中间一般会设计一“拉杆”，是为了形成三角形，利用三角形具有稳定性来增加其稳定性，
故选：D．
5．如图所示，一个正方形水池的四周恰好被4个正n边形地板砖铺满，则n等于（　　）

A．4 B．6 C．8 D．10
【分析】根据平面镶嵌的条件，先求出正n边形的一个内角的度数，再根据内角和公式求出n的值．
【解答】解：正n边形的一个内角＝（360°﹣90°）÷2＝135°，则
135°n＝（n﹣2）180°，
解得n＝8．
故选：C．
6．二元一次方程2x+3y＝11的正整数解有（　　）
A．2组 B．3组 C．4组 D．5组
【分析】先变形二元一次方程，用含一个字母的代数式表示另一个字母，根据奇偶性，可得结论．
【解答】解：原方程可变形为：x＝，
由于方程的解是正整数，
所以y为不大于3的奇数．
当y＝1时，x＝4；
当y＝3时，x＝1；
所以满足条件的正整数有两组．
故选：A．
7．如图，在△ABC中，∠BAC＝65°，∠C＝20°，将△ABC绕点A逆时针旋转n度（0＜n＜180）得到△ADE，若DE∥AB，则n的值为（　　）

A．65 B．75 C．85 D．130
【分析】根据三角形内角和定理求出∠ABC，根据旋转得出∠EDA＝∠ABC＝95°，根据平行四边形的性质求出∠DAB即可．
【解答】解：∵在△ABC中，∠BAC＝65°，∠C＝20°，
∴∠ABC＝180°﹣∠BAC﹣∠C＝180°﹣65°﹣20°＝95°，
∵将△ABC绕点A逆时针旋转n角度（0＜n＜180°）得到△ADE，
∴∠ADE＝∠ABC＝95°，
∵DE∥AB，
∴∠ADE+∠DAB＝180°，
∴∠DAB＝180°﹣∠ADE＝85°，
∴旋转角n的度数是85°，
故选：C．
8．已知等腰三角形的两边长分别为a，b，且a，b满足+（2a+3b﹣13）2＝0，则此等腰三角形的周长为（　　）
A．7或8 B．6或10 C．6或7 D．7或10
【分析】首先根据+（2a+3b﹣13）2＝0求得a、b的值，然后求得等腰三角形的周长即可．
【解答】解：∵+（2a+3b﹣13）2＝0，
∴
解得：，
当a为底时，三角形的三边长为2，3，3，则周长为8；
当b为底时，三角形的三边长为2，2，3，则周长为7．
故选：A．
9．《九章算术》是我国东汉初年编订的一部数学经典著作．在它的“方程”一章里，一次方程组是由算筹布置而成的．《九章算术》中的算筹图是竖排的，现在我们把它改为横排，如图1、图2．图中各行从左到右列出的算筹数分别表示未知数x，y的系数与相应的常数项．把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来，就是，类似地，图2所示的算筹图我们可以表述为（　　）

A． B．
C． D．
【分析】由图1可得1个竖直的算筹数算1，一个横的算筹数算10，每一横行是一个方程，第一个数是x的系数，第二个数是y的系数，第三个数是相加的结果：前面的表示十位，后面的表示个位，由此可得图2的表达式．
【解答】解：第一个方程x的系数为2，y的系数为1，相加的结果为11；第二个方程x的系数为4，y的系数为3，相加的结果为27，所以可列方程组为：
，
故选：C．
10．如图，已知四边形ABCD中，∠B＝98°，∠D＝62°，点E、F分别在边BC、CD上．将△CEF沿EF翻折得到△GEF，若GE∥AB，GF∥AD，则∠C的度数为（　　）

A．80° B．90° C．100° D．110°
【分析】依据平行线的性质，即可得到∠CEG＝∠B＝98°，∠CFG＝∠D＝62°，再根据四边形内角和进行计算即可．
【解答】解：∵GE∥AB，GF∥AD，
∴∠CEG＝∠B＝98°，∠CFG＝∠D＝62°，
由折叠可得，∠C＝∠G，
∴四边形CEGF中，∠C＝（360°﹣98°﹣62°）＝100°，
故选：C．
11．关于x的不等式组的整数解共有5个，则a的取值范围是（　　）
A．a＝﹣3 B．﹣4＜a＜﹣3 C．﹣4≤a＜﹣3 D．﹣4＜a≤﹣3
【分析】首先解不等式组确定不等式组的解集，然后根据不等式组的整数解有5个，即可得到一个关于a的不等式组，解不等式组即可求解．
【解答】解：，
解①得：x≥a，
解②得：x＜2，
则不等式组的解集是：a≤x＜2，
不等式组有5个整数解，则﹣4＜a≤﹣3，
故选：D．
12．在直角三角形ABC中，∠C＝90°，AD平分∠BAC交BC于点D，BE平分∠ABC交AC于点E，AD、BE相交于点F，过点D作DG∥AB，过点B作BG⊥DG交DG于点G．下列结论：①∠AFB＝135°；②∠BDG＝2∠CBE；③BC平分∠ABG；④∠BEC＝∠FBG．其中正确的个数是（　　）

A．1个 B．2个 C．3个 D．4个
【分析】根据三角形内角和定理以及平行线的性质，即可判定①②正确；根据等角的余角相等，即可判定④正确．
【解答】解：∵AD平分∠BAC交BC于点D，BE平分∠ABC交AC于点E，
∴∠BAF＝∠BAC，∠ABF＝∠ABC，
又∵∠C＝90°，
∴∠ABC+∠BAC＝90°，
∴∠BAF+∠ABF＝45°，
∴∠AFB＝135°，故①正确；
∵DG∥AB，
∴∠BDG＝∠ABC＝2∠CBE，故②正确；
∵∠ABC的度数不确定，
∴BC平分∠ABG不一定成立，故③错误；
∵BE平分∠ABC，
∴∠ABF＝∠CBE，
又∵∠C＝∠ABG＝90°，
∴∠BEC+∠CBE＝90°，∠ABF+∠FBG＝90°，
∴∠BEC＝∠FBG，故④正确．
故选：C．

二、填空题（本大题6个小题，每小题3分，共18分）
13．（3分）若一个正多边形的一个内角等于140°，那么这个多边形是正　九　边形．
【分析】一个正多边形的每个内角都相等，根据内角与外角互为邻补角，因而就可以求出外角的度数．根据任何多边形的外角和都是360°，利用360°除以外角的度数就可以求出外角和中外角的个数，即多边形的边数．
【解答】解：∵内角与外角互为邻补角，
∴正多边形的一个外角是180°﹣140°＝40°，
∵多边形外角和为360°，
∴360°÷40°＝9，
则这个多边形是九边形．
故答案为：九．
14．（3分）如图，已知△ABC≌△ADE，若AB＝7，AC＝3，则BE的值为　4　．

【分析】根据△ABC≌△ADE，得到AE＝AC，由AB＝7，AC＝3，根据BE＝AB﹣AE即可解答．
【解答】解：∵△ABC≌△ADE，
∴AE＝AC，
∵AB＝7，AC＝3，
∴BE＝AB﹣AE＝AB﹣AC＝7﹣3＝4．
故答案为：4．
15．（3分）若关于x的方程（k﹣2）x|k﹣1|+5k+1＝0是一元一次方程，则k＝　0　．
【分析】根据x的次数为1，x的系数不等于0，计算即可．
【解答】解：根据题意得：，
解得：k＝0，
故答案为：0．
16．（3分）若不等式组的解集为2＜x＜3，则（a+b）2021＝　1　．
【分析】分别求出每一个不等式的解集，根据不等式组的解集得出a、b的值，代入计算即可．
【解答】解：由x﹣b＜0，得：x＜b，
由x+a＞0，得：x＞﹣a，
∵不等式组的解集为2＜x＜3，
∴﹣a＝2，b＝3，
则a＝﹣2，
∴（a+b）2021＝（﹣2+3）2021＝12021＝1，
故答案为：1．
17．（3分）按下面的程序计算，若开始输入的x值为正数，最后输出的结果为53，请写出符合条件的所有x的值 　1、5、17　．

【分析】根据输出结果，由运算顺序，列一元一次方程求出结果．
【解答】解：根据题意得：3x+2＝53，
解得，x＝17．
根据题意得：3x+2＝17，
解得，x＝5．
根据题意得：3x+2＝5，
解得，x＝1．
故答案为：1、5、17．
18．（3分）如图，长方形ABCD中，AB＝4，AD＝2．点Q与点P同时从点A出发，点Q以每秒1个单位的速度沿A→D→C→B的方向运动，点P以每秒3个单位的速度沿A→B→C→D的方向运动，当P，Q两点相遇时，它们同时停止运动．设Q点运动的时间为x（秒），在整个运动过程中，当△APQ为直角三角形时，则相应的x的值或取值范围是　0＜x≤或x＝2　．

【分析】由题意可得当0＜x≤△AQM是直角三角形，当 ＜x＜2时△AQM是锐角三角形，当x＝2时，△AQM是直角三角形，当2＜x＜3时△AQM是钝角三角形．
【解答】解：当点P在AB上时，点Q在AD上时，此时△APQ为直角三角形，则0＜x≤；
当点P在BC上时，点Q在AD上时，此时△APQ为锐角三角形，则＜x＜2；
当点P在C处，此时点Q在D处，此时△APQ为直角三角形，则x＝2时；
当点P在CD上时，点Q在DC上时，此时△APQ为钝角三角形，则2＜x＜3．
故答案是：0＜x≤或x＝2．
三、解答题（本大题8个小题，共84分）
19．（10分）（1）解方程：2+5x＝8+3x．
（2）解不等式组，并把解集在数轴上表示出来．
【分析】（1）移项、合并同类项、系数化为1即可；
（2）分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集．
【解答】解：（1）移项，得：5x﹣3x＝8﹣2，
合并同类项，得：2x＝6，
系数化为1，得：x＝3；

（2）解不等式①，得：x≤2，
解不等式②，得：x≥﹣1，
则不等式组的解集为﹣1≤x≤2，
将不等式组的解集表示在数轴上如下：

20．（8分）甲、乙两位同学在解关于x、y的方程组时，甲同学看错a得到方程的解为，乙同学看错b得到方程组的，求x+y的值．
【分析】把代入bx﹣y＝2可求出b的值，把代入2x+ay＝1可求出a的值，把a、b的值代入原方程组即可求出x、y的值，进而求出x+y的值．
【解答】解：把代入bx﹣y＝2得：3b﹣4＝2，
解得：b＝2，
把代入2x+ay＝1得：4﹣3a＝1，
解得：a＝1，
∴原方程组为，
解得：，
∴x+y＝＝．
21．（10分）如图所示的正方形网格中，每个小正方形的边长均为1个单位，△ABC的三个顶点都在格点上．
（1）在网格中画出△ABC向下平移3个单位得到的△A1B1C1；
（2）在网格中画出△ABC关于直线m对称的△A2B2C2；
（3）在直线m上画一点P，使得C1P+C2P的值最小．

【分析】（1）根据图形平移的性质画出△A1B1C1即可；
（2）根据轴对称的性质画出△ABC关于直线m对称的△A2B2C2即可；
（3）连接C1C2交直线m于点P，则点P即为所求点．
【解答】解：（1）如图，△A1B1C1即为所求；

（2）如图，△A2B2C2即为所求；

（3）连接C1C2交直线m于点P，则点P即为所求点．

22．（10分）已知关于x、y的方程组中，x为非负数、y为负数．
（1）试求m的取值范围；
（2）当m取何整数时，不等式3mx+2x＞3m+2的解集为x＜1．
【分析】（1）把m看作常数，解方程组，根据x为非负数、y为负数，列不等式组解出即可；
（2）根据不等式3mx+2x＞3m+2的解为x＜1，求出m的取值范围，综合①即可解答．
【解答】解：（1），
①+②得：2x＝18﹣4m，x＝9﹣2m，
①﹣②得：﹣2y＝4+2m，y＝﹣2﹣m，
∵x为非负数、y为负数，
∴，解得：﹣2＜m≤；
（2）3mx+2x＞3m+2，
（3m+2）x＞3m+2，
∵不等式3mx+2x＞3m+2的解为x＜1，
∴3m+2＜0，
∴m＜﹣，
由（1）得：﹣2＜m≤，
∴﹣2＜m＜﹣，
∵m整数，
∴m＝﹣1；
即当m＝﹣1时，不等式3mx+2x＞3m+2的解为x＜1．
23．（10分）如图，在△ABC中，CM⊥AB于点M，∠ACB的平分线CN交AB于点N，过点N作ND∥AC交BC点D．若∠A＝78°，∠B＝50°．求：
（1）∠CND的度数；
（2）∠MCN的度数．

【分析】（1）求出∠ACN，利用平行线的性质解决问题即可．
（2）利用直角三角形的两锐角互余解决问题即可．
【解答】（1）解：在△ABC中，∵∠A＝78°，∠B＝50°，
∴∠ACB＝52°，
又∵CN平分∠ACB，
∴∠ACN＝∠ACB＝26°，
∵ND∥AC，
∴∠CND＝∠ACN＝26°．

（2）在△ACN中，∠ANC＝180°﹣（∠A+∠ACN）＝180°﹣（78°+26°）＝76°，
又∵CM⊥AB，
∴∠MCN＝90°﹣76°＝14°．
24．（10分）某中学计划购买A型和B型课桌凳共200套．经招标，购买一套A型课桌凳比购买一套B型课桌凳少用40元，且购买4套A型和5套B型课桌凳共需1820元．
（1）求购买一套A型课桌凳和一套B型课桌凳各需多少元？
（2）学校根据实际情况，要求购买这两种课桌凳总费用不能超过40880元，并且购买A型课桌凳的数量不能超过B型课桌凳数量的，求该校本次购买A型和B型课桌凳共有几种方案？哪种方案的总费用最低？
【分析】（1）根据购买一套A型课桌凳比购买一套B型课桌凳少用40元，以及购买4套A型和5套B型课桌凳共需1820元，得出等式方程求出即可；
（2）利用要求购买这两种课桌凳总费用不能超过40880元，并且购买A型课桌凳的数量不能超过B型课桌凳数量的，得出不等式组，求出a的值即可，再利用一次函数的增减性得出答案即可．
【解答】解：（1）设A型每套x元，则B型每套（x+40）元．
由题意得：4x+5（x+40）＝1820．
解得：x＝180，x+40＝220．
即购买一套A型课桌凳和一套B型课桌凳各需180元、220元；

（2）设购买A型课桌凳a套，则购买B型课桌凳（200﹣a）套．
由题意得：，
解得：78≤a≤80．
∵a为整数，
∴a＝78、79、80．
∴共有3种方案，
设购买课桌凳总费用为y元，
则y＝180a+220（200﹣a）＝﹣40a+44000．
∵﹣40＜0，y随a的增大而减小，
∴当a＝80时，总费用最低，此时200﹣a＝120，
即总费用最低的方案是：购买A型80套，购买B型120套．
25．（12分）定义：对于任何有理数m，符号【m】表示不大于m的最大整数．例如：【4.5】＝4，【8】＝8，【﹣3.2】＝﹣4．
（1）填空：【π】＝　3　，【﹣2.1】+【5.1】＝　2　．
（2）求方程4x﹣3【x】+5＝0的整数解；
（3）如果【】＝﹣4，求满足条件的x的取值范围．
【分析】（1）根据题目所给信息求解；
（2）整理方程得【x】＝，根据定义得出x﹣1＜≤x，解不等式组求得x的取值范围，由[x]是整数，设4x+5＝3n（n是整数）得到x＝，则﹣8＜≤﹣5，解得﹣9＜n≤﹣5，即可求得当n＝﹣5，方程的整数解为x＝﹣5；
（3）根据题意得出：﹣4≤＜﹣3，求出x的取值范围．
【解答】解：（1）由题意得：【π】＝3，【﹣2.1】+【5.1】＝﹣3+5＝2，
故答案为3，2；

（2）∵4x﹣3【x】+5＝0，
∴【x】＝，
∴x﹣1＜≤x，
解得不等式组的解集为：﹣8＜x≤﹣5，
∵【x】是整数，
设4x+5＝3n（n是整数），
∴x＝，
∴﹣8＜≤﹣5，
解得不等式组的解集为：﹣9＜n≤﹣5，
∵n是整数，
∴n为﹣8，﹣7，﹣6，﹣5，
∴当n＝﹣5，方程的整数解为x＝﹣5；

（3）根据题意得：﹣4≤＜﹣3，
解得：7＜x≤，
则满足条件的x的取值范围为7＜x≤．
26．（14分）如图1，点D为△ABC边BC的延长线上一点．
（1）若∠A：∠ABC＝3：4，∠ACD＝140°，求∠A的度数；
（2）若∠ABC的角平分线与∠ACD的角平分线交于点M，过点C作CP⊥BM于点P．求证：∠MCP＝90°﹣∠A；
（3）在（2）的条件下，将△MBC以直线BC为对称轴翻折得到△NBC，∠NBC的角平分线与∠NCB的角平分线交于点Q（如图2），试探究∠BQC与∠A有怎样的数量关系，请写出你的猜想并证明．

【分析】（1）先根据∠A：∠ABC＝3：4，设∠A＝3k，∠ABC＝4k，再由三角形外角的性质求出k的值，进而可得出结论；
（2）根据三角形外角的性质得出∠M＝∠MCD﹣∠MBC，∠A＝∠ACD﹣∠ABC．再由MC、MB分别平分∠ACD、∠ABC得出∠MCD＝∠ACD，∠MBC＝∠ABC，故∠M＝（∠ACD﹣∠ABC）＝∠A．根据CP⊥BM即可得出结论；
（3）根据BQ平分∠CBN，CQ平分∠BCN可知∠QBC＝∠CBN，∠QCB＝∠BCN，再根据三角形内角和定理可知，∠Q＝180°﹣（∠CBN+∠BCN）＝（180°﹣∠N）＝90°+∠N．由（2）知：∠M＝∠A．根据轴对称性质知：∠M＝∠N，由此可得出结论．
【解答】（1）解：∵∠A：∠ABC＝3：4，
∴可设∠A＝3k，∠ABC＝4k，
又∵∠ACD＝∠A+∠ABC＝140°，
∴3k+4k＝140°，
解得k＝20°．
∴∠A＝3k＝60°．

（2）证明：∵∠MCD是△MBC的外角，
∴∠M＝∠MCD﹣∠MBC．
同理可得，∠A＝∠ACD﹣∠ABC．
∵MC、MB分别平分∠ACD、∠ABC，
∴∠MCD＝∠ACD，∠MBC＝∠ABC，
∴∠M＝（∠ACD﹣∠ABC）＝∠A．
∵CP⊥BM，
∴∠PCM＝90°﹣∠M＝90°﹣∠A．

（3）猜想∠BQC＝90°+∠A．
证明如下：
∵BQ平分∠CBN，CQ平分∠BCN，
∴∠QBC＝∠CBN，∠QCB＝∠BCN，
∴∠Q＝180°﹣（∠CBN+∠BCN）＝（180°﹣∠N）＝90°+∠N．
由（2）知：∠M＝∠A．
又由轴对称性质知：∠M＝∠N，
∴∠BQC＝90°+∠A．