华师大版八年级下册18.1 平行四边形的性质图片课件ppt

这是一份华师大版八年级下册18.1 平行四边形的性质图片课件ppt，文件包含1811平行四边形的性质pptx、1811平行四边形的性质--练习docx、1811平行四边形的性质--教案docx、1811平行四边形的性质--学案doc等4份课件配套教学资源，其中PPT共25页， 欢迎下载使用。
平行四边形是我们常见的一种图形，它具有十分和谐的对称美.它是什么样的对称图形呢？它具有哪些性质,又如何识别平行四边形呢？读下去，你就会发现这些答案了.
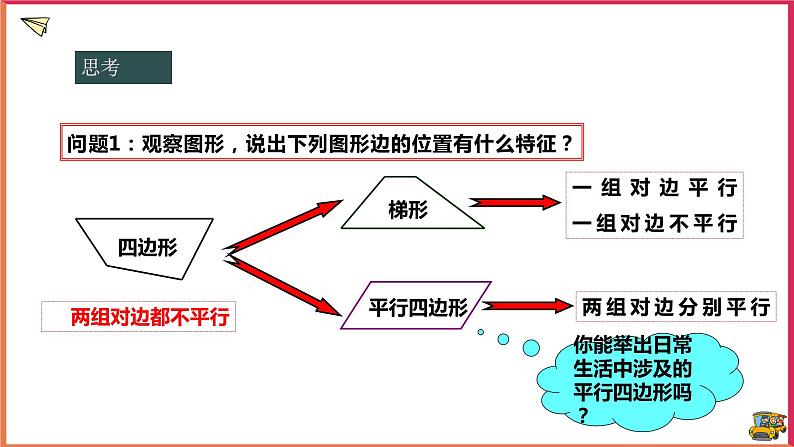
问题1：观察图形，说出下列图形边的位置有什么特征？
一组对边平行一组对边不平行
你能举出日常生活中涉及的平行四边形吗？
观察下列生活的平行四边形物体，你能说说什么是平行四边形吗？
请你给平行四边形给个完整的定义哟！
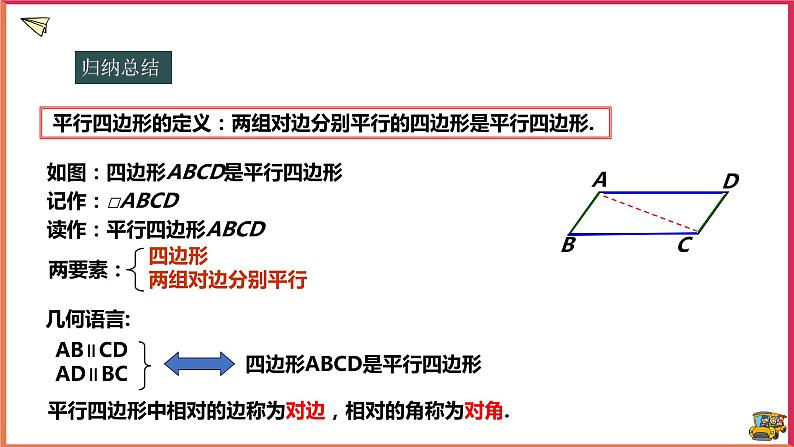
平行四边形的定义：两组对边分别平行的四边形是平行四边形.
如图：四边形ABCD是平行四边形记作：□ABCD 读作：平行四边形ABCD
四边形ABCD是平行四边形
AB∥CD AD∥BC
平行四边形中相对的边称为对边，相对的角称为对角.
根据定义，平行四边形的一个主要性质是：
由此可知，平行四边形的相邻两个内角互补.
除此之外，平行四边形的边、角还有什么性质呢？
平行四边形是否是中心对称图形？
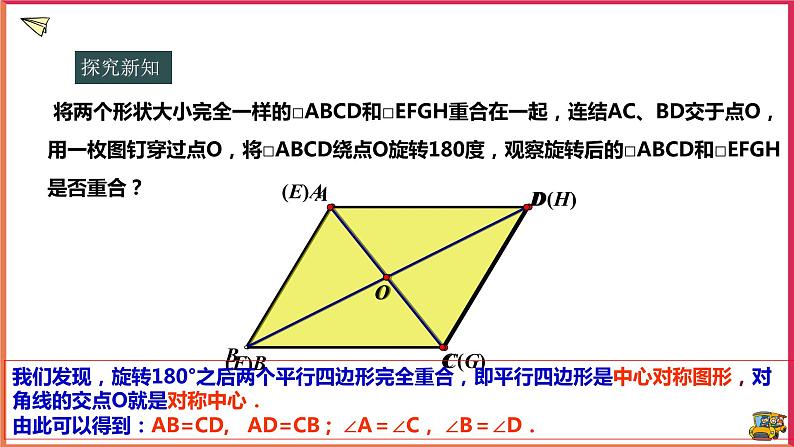
将两个形状大小完全一样的□ABCD和□EFGH重合在一起，连结AC、BD交于点O，用一枚图钉穿过点O，将□ABCD绕点O旋转180度，观察旋转后的□ABCD和□EFGH是否重合？
我们发现，旋转180°之后两个平行四边形完全重合，即平行四边形是中心对称图形，对角线的交点O就是对称中心．由此可以得到：AB=CD, AD=CB ; ∠A＝∠C， ∠B＝∠D．
1.平行四边形的边具有哪些性质？说说你的理由。
2.平行四边形的角具有哪些性质？说说你的理由。
平行四边形的对边相等；平行四边形的对角相等.
AD//BCAB//CD
△ABD ≌ △CDB
∠A=∠CAB=CDAD=BC
已知：如图，□ABCD.
求证：AB=CD，AD=BC，∠A=∠C，∠ABC=∠CDA.
证明：连结BD.∵四边形ABCD是平行四边形，∴AB∥DC，AD∥BC(平行四边形的两组对边分别平行)，∴∠ABD=∠CDB， ∠ADB=∠CBD.又∵ BD=DB，∴△ABD ≌△CDB.∴ AB=CD，AD=BC， ∠A=∠C.由∠ABD=∠CDB和∠ADB=∠CBD，得∠ABC=∠CDA.
平行四边形的对边相等；
平行四边形的对角相等；
∵四边形ABCD是平行四边形
平行四边形的对边平行；
例1、如图，在□ABCD中，已知∠A=40°， 求其他各内角的大小.
解：在□ABCD中，∠A=∠C， ∠B=∠D（平行四边形的对角相等）.∵ ∠A=40°∴ ∠C=40°又∵AD // BC∴∠A+∠B=180°∴∠B=180°-∠A=180°-40°=140°∴ ∠D=∠B=140°
在□ABCD中∠A:∠B:∠C:∠D的值可能是（ ）A.1:2:3:4 B.1:2:2:1 C.2:2:1:1 D.2:1:2:1
例2 如图，在□ABCD中，已知AB=8，周长等于24，求其余三条边的长.
在笔直的铁轨上，夹在两根铁轨之间的枕木是否一样长？
(2)试一试：准备一张方格纸，按下面的步骤完成如下作图并按要求回答问题：
问题1：经过测量你发现MM’、NN’、QQ’，┄的长度有何关系？问题2：在直线AB上再取一点E，试一试.
两条平行线间的距离： 两条平行线中，一条直线上任意一点到另一条直线的距离.本质：点到直线的距离
两条平行线间的距离的性质：两条平行线之间的距离处处相等.
∵m // n，AB、CD、EF 垂直于 n，交n于B、D、F，交 m于A、C、E.∴AB=CD=EF
例3 已知平行四边形的周长是24，相邻两边的长度相差4，求该平行四边形相邻两边的长．
解：设AB的长为 x ,则BC的长为 x+4.根据已知，可得 2（AB+BC）=24,即 2（x+x+4）=24, 4x+8=24,解得 x=4.所以，该平行四边形相邻两边的长分别为4和8.
已知平行四边形ABCD的周长为60cm，两邻边AB，BC长的比为3：2，求AB和BC的长度 .
解：∵在□ABCD中, 对边相等, 又∵□ABCD的周长为60cm. ∴AB + BC=30cm 又AB：BC=3：2，即AB=1.5BC 则 1.5BC + BC=30 , 解得 BC=12 (cm) 而 AB=1.5×12=18 (cm)
例4 已知：如图，在▱ABCD中，∠ADC的平分线与AB相交于点E.求证：BE＋BC＝CD.
证明：∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD，∴∠CDE=∠AED，又∵DE是∠ADC的平分线，∴∠ADE=∠CDE，∴∠ADE=∠AED ∴AD=AE.又∵ AD=BC(平行四边形的对边相等)，∴ AE=BC.∴BE+BC=BE+AE=AB=CD.
下列说法：①平行四边形具有一般四边形的性质；②平行四边形相邻两角互补;③平行四边形的对角相等；④平行四边形的对边相等.其中正确的个数为 （ ） A.1个 B.2个 C.3个 D.4个2.如图，在□ABCD中，DE平分∠ADC，AD=8，BE=3，则□ABCD的周长是（ ） A.16 B.14 C.26 D.24
3.在□ABCD中, ∠A=65°, 则∠B= °, ∠C= °, ∠D= °.
4.在□ABCD中, AB+CD=28cm. □ABCD的周长等于96cm, 则 AB= , BC= , CD= , AD= .
5.已知平行四边形ABCD中, ∠1=15°, ∠2=25°,且AB=5cm，AO=2cm，求∠DAB和∠ABC的度数，并找出长度分别为5cm和2cm的线段.
解: ∵在□ABCD中，AB∥DC ∴∠ABD＝∠1= 15° ∴∠ABC＝15°+ 25°= 40 ° 则∠DAB＝180°- 40°= 140 ° 而 DC=AB= 5cm, CO=AO= 2cm .
6. 如图所示,在▱ABCD中,若∠A∶∠B=1∶3,求∠D的度数.