华师大版八年级下册第18章 平行四边形18.2 平行四边形的判定课文ppt课件

这是一份华师大版八年级下册第18章 平行四边形18.2 平行四边形的判定课文ppt课件，文件包含1822平行四边形的判定pptx、1822平行四边形的判定--练习docx、1822平行四边形的判定--教案docx、1822平行四边形的判定--学案doc等4份课件配套教学资源，其中PPT共26页， 欢迎下载使用。
1.同学们，我们学习了平行四边形的判定方法，它们有哪些呢？请大家忆一忆，并请一位同学回答。
1、两组对边分别平行的四边形是平行四边形2、两组对边分别相等的四边形是平行四边形3、一组对边平行且相等的四边形是平行四边形
某装饰店要招聘店员，老板出了这样一道考题：“一顾客要一块平行四边形的玻璃，你能否利用手头工具，一长一短的两根小木棒，画出一个平行四边形玻璃，并说明这块玻璃符合顾客要求的道理。”你能为招聘人员设计一方案吗？
1.平行四边形的对角线具有什么性质？
2. “平行四边形的对角线互相平分”这个命题的逆命题是什么？对角线互相平分的四边形是平行四边形．3.试着找出上述命题中的题设和结论，并画出图形，写出已知、求证。
平行四边形的对角线互相平分
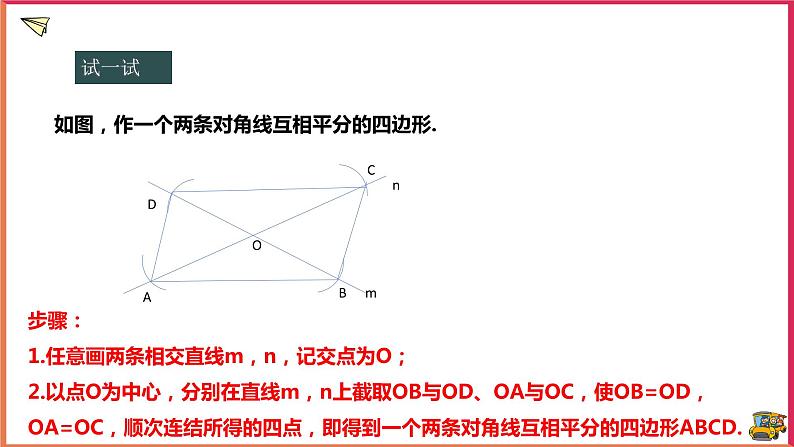
如图，作一个两条对角线互相平分的四边形.
步骤：1.任意画两条相交直线m，n，记交点为O；2.以点O为中心，分别在直线m，n上截取OB与OD、OA与OC，使OB=OD，OA=OC，顺次连结所得的四点，即得到一个两条对角线互相平分的四边形ABCD.
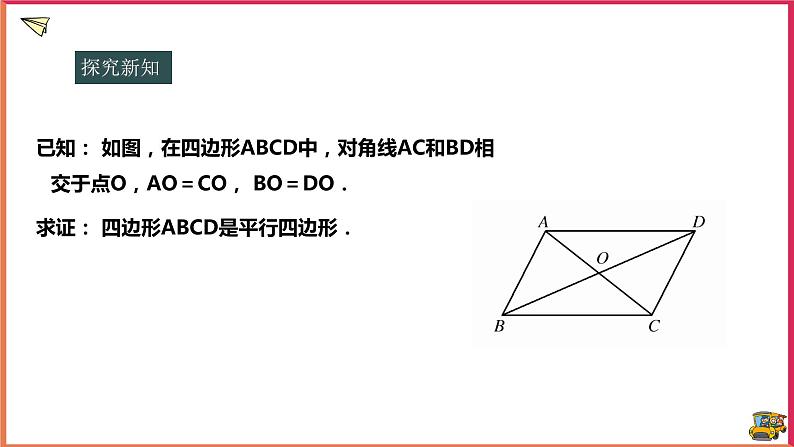
已知： 如图，在四边形ABCD中，对角线AC和BD相交于点O，AO＝CO， BO＝DO．求证： 四边形ABCD是平行四边形．
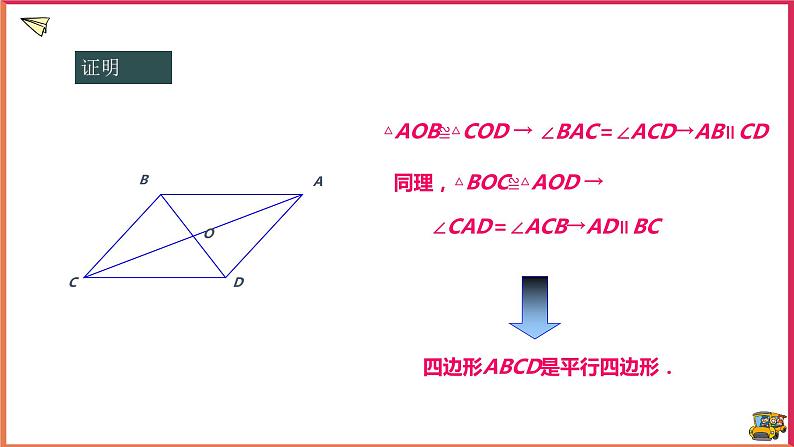
△AOB≌△COD →
∠BAC＝∠ACD→AB∥CD
∠CAD＝∠ACB→AD∥BC
同理，△BOC≌△AOD →
四边形ABCD是平行四边形．
判定定理四： 对角线互相平分的四边形是平行四边形．
∴ 四边形ABCD是平行四边形. （对角线互相平分的四边形是平行四边形）
∵ A0=C0, BO=DO
1．在给定条件下，能画出平行四边形的是( )A．以20 cm、36 cm为对角线，22 cm为一条边B．以6 cm、10 cm为对角线，2 cm为一条边C．以60 cm为一条对角线，20 cm、34 cm为两条邻边D．以6 cm为一条对角线，3 cm、10 cm为两条邻边
∵四边形ABCD是平行四边形 ∴ AO=CO，BO=DO ∵AE=CF ∴AO－AE=CO－CF ∴EO=FO 又 BO=DO ∴ 四边形BFDE是平行四边形
证明：连接对角线BD，交AC于点O
例2、已知：E、F是平行四边形ABCD对角线AC上的两点，并且AE=CF．求证：四边形BFDE是平行四边形．
∴△AED ≌△CFB(SAS)∴DE=BF同理可证：BE=DF四边形BFDE是平行四边形．
两组对边分别平行的四边形是平行四边形两组对边分别相等的四边形是平行四边形一组对边平行且相等的四边形是平行四边形
两条对角线互相平分的四边形是平行四边形
例3：如图，在□ABCD中，点F，H分别在边AB，CD上，且BF=DH.求证：AC和HF互相平分.
证明：连结AH、CF∵四边形ABCD是平行四边形∴AB//CD,AB=CD又∵BF=DH∴AB-BF=CD-DH即AF=CH∴四边形AFCH是平行四边形∴AC和HF互相平分
例4：如图，在四边形ABCD中，∠A=∠C，∠B=∠D.求证：四边形ABCD是平行四边形
证明：在四边形ABCD中，∵∠A+∠B+∠C+∠D=360°且∠A=∠C，∠B=∠D∴∠A+∠B+∠A+∠B=360°即2（∠A+∠B）=360°∴∠A+∠B=180°∴AD//CB.同理可证：AB//CD∴四边形ABCD是平行四边形
通过这个题目，你有什么发现？
∵∠A=∠C，∠B=∠D，
∴四边形ABCD是平行四边形．
两组对角分别相等的四边形是平行四边形．
平行四边形的判定定理:
例5、四边形AEFD和EBCF都是平行四边形，求证四边形ABCD是平行四边形。
证明：∵四边形AEFD是平行四边形∴AD∥EF，AD=EF
又∵四边形EBCF是平行四边形∴EF∥BC,EF=BC
∴AD∥BC,AD=BC
∴四边形ABCD是平行四边形。
例6、如图，G、H是□ABCD对角线AC上的两点，且AG=CH，E，F分别是边AB和CD的中点.求证：四边形EHFG是平行四边形.
证明：连接EF交AC于点O∵四边形ABCD是平行四边形∴AB∥CD,AB=CD又∵E,F是AB,CD的中点。∴AE=CF又∵ AB∥CD,∠EAO=∠FCO在△EAO与△COF中
∵∠EAO=∠FCO∠AOE=∠COFAE=CF∴△AOE≌△COF∴OE=OF，OA=OC又∵AC=CH∴OC=OH∴四边形EHFG是平行四边形(对角线互相平分的四边形是平行四边形)
现在我们总共学习了多少种判定平行四边形的方法(包括定义)？这些判定方法与平行四边形的性质之间，又有怎样的关系呢？
平行四边形的判定方法有5种
判定方法和平行四边形的性质互为逆定理.
1．能够判定一个四边形是平行四边形的条件是( )A．一组对边相等 B．两条对角线互相垂直C．两条对角线互相平分 D．一组对边平行2．如图，在四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是( )A．AB∥CD，∠DAO＝∠BCO B．AB∥CD，∠BAO＝∠DCOC．AO＝CO，BO＝DO D．AB＝CD，∠BAO＝∠DCO
3．如图，AD为△ABC的中线，AB＝9，AC＝12，延长AD至点E，使DE＝AD，连结BE、CE，则四边形ABEC的周长是_________．4.木匠通常取两根木棒的中点进行加固，则得到的虚线四边形是___________________，理由是________________________________________________________．
对角线互相平分的四边形是平行四边形
5．如图，在四边形ABCD中，AC与BD相交于点O，AB∥CD，OA＝OC.求证：四边形ABCD是平行四边形．
证明：∵AB∥CD，∴∠ABO＝∠CDO，∠BAO＝∠DCO.又∵OA＝OC，∴△AOB≌△COD，∴OB＝OD.又∵OA＝OC，∴四边形ABCD为平行四边形．