资料中包含下列文件,点击文件名可预览资料内容







还剩17页未读,
继续阅读
华师大版八年级下册2. 菱形的判定评课ppt课件
展开
这是一份华师大版八年级下册2. 菱形的判定评课ppt课件,文件包含1922菱形的判定ppt、1922菱形的判定--练习doc、1922菱形的判定--学案doc、1922菱形的判定--教案doc等4份课件配套教学资源,其中PPT共25页, 欢迎下载使用。
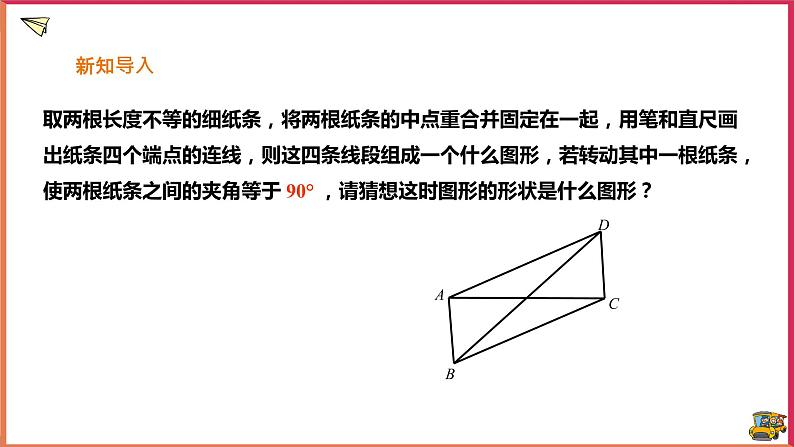
取两根长度不等的细纸条,将两根纸条的中点重合并固定在一起,用笔和直尺画出纸条四个端点的连线,则这四条线段组成一个什么图形,若转动其中一根纸条,使两根纸条之间的夹角等于 90° ,请猜想这时图形的形状是什么图形?
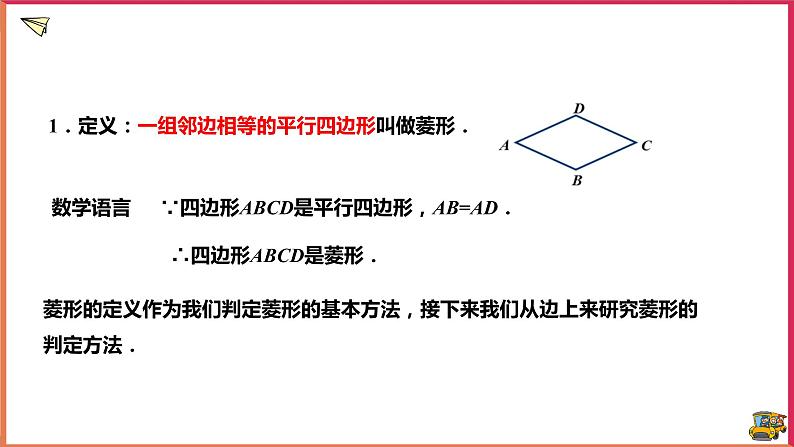
1.定义:一组邻边相等的平行四边形叫做菱形.
菱形的定义作为我们判定菱形的基本方法,接下来我们从边上来研究菱形的判定方法.
∵四边形ABCD是平行四边形,AB=AD.
∴四边形ABCD是菱形.
四条边相等的四边形是菱形.
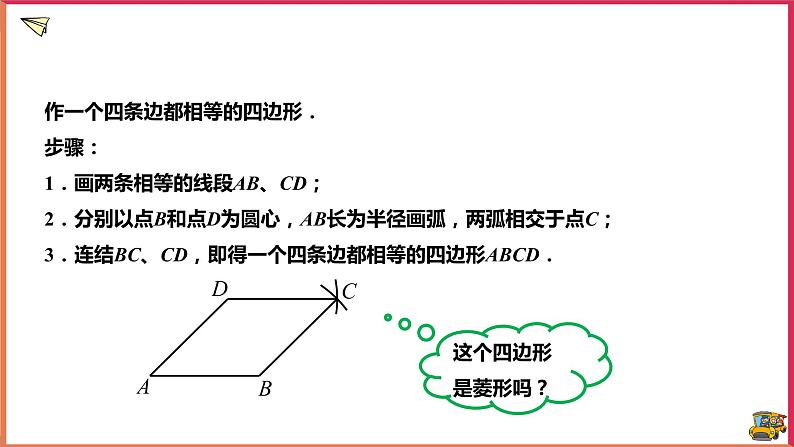
作一个四条边都相等的四边形.步骤:1.画两条相等的线段AB、CD;2.分别以点B和点D为圆心,AB长为半径画弧,两弧相交于点C;3.连结BC、CD,即得一个四条边都相等的四边形ABCD.
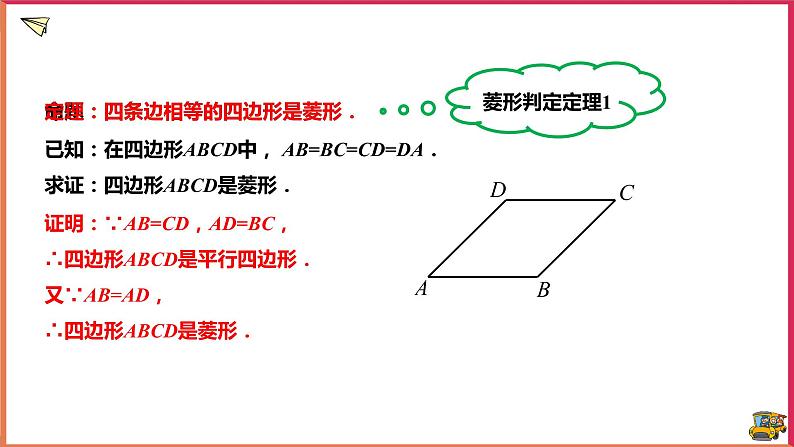
命题:四条边相等的四边形是菱形.
已知:在四边形ABCD中, AB=BC=CD=DA.求证:四边形ABCD是菱形.
证明:∵AB=CD,AD=BC,∴四边形ABCD是平行四边形.又∵AB=AD,∴四边形ABCD是菱形.
定理:四条边相等的四边形是菱形.
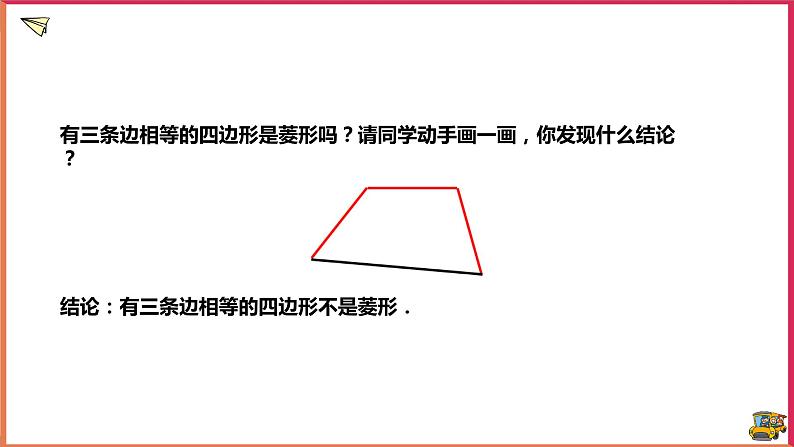
有三条边相等的四边形是菱形吗?请同学动手画一画,你发现什么结论?
结论:有三条边相等的四边形不是菱形.
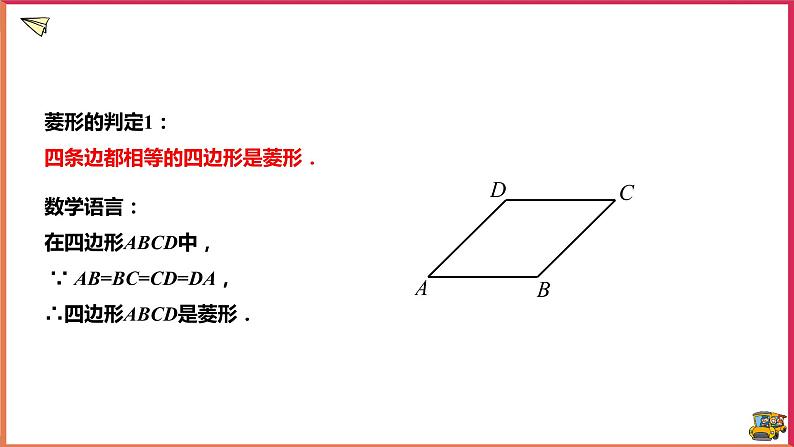
数学语言:在四边形ABCD中, ∵ AB=BC=CD=DA,∴四边形ABCD是菱形.
菱形的判定1:四条边都相等的四边形是菱形.
例4 如图,在矩形ABCD中,点E、F、G、H分别是四条边的中点,试问四边形EFGH是什么图形?并说明理由.
若四边形ABCD的对角线AC⊥BD,则四边形ABCD是不是菱形?
结论:对角线互相垂直的四边形不能判定为菱形.
对角线互相垂直的平形四边形是菱形吗?
作一个两条对角线互相垂直的平行四边形.步骤:1.作两条互相垂直的直线m,n,记交点为点O;2.以点O为圆心,适当长为半径画弧,在直线m上截取相等的两条线段OA、OC;3.以点O为圆心,另一适当长为半径画弧,在直线n上截取相等的两条线段OB、OD;4.顺次连结所行的四点,即得一个对角线互相垂直且平分的四边形ABCD,显然,它是一个对角线互相垂直的平行四边形.
这个平行四边形是菱形吗?
命题:对角线互相垂直的平行四边形是菱形.
已知:在平行四边形ABCD中,AC⊥BD .求证:平行四边形ABCD是菱形.
证明:∵四边形ABCD是平行四边形,∴OA=OC.又∵AC⊥BD,∴BA=BC, ∴ 平行四边形ABCD是菱形.(有一组邻边相等的平行四边形是菱形)
定理:对角线互相垂直的平行四边形是菱形.
数学语言:∵在□ABCD中,AC⊥BD,∴ □ABCD是菱形.
菱形的判定2:对角线互相垂直的平行四边形是菱形.
这四条线段组成平行四边形,理由:对角线互相平分的四边形是平行四边形.当两根纸条之间的夹角等于 90° 时,这时图形是菱形,理由:对角线互相垂直的平行四边形是菱形.
例5 如图,已知矩形ABCD的对角线AC的垂直平分线与边AD 、BC分别交于E、F. 求证:四边形AFCE是菱形.
分析:要证四边形AFCE是菱形,由已知条件可知EF⊥AC,所以只需证明四边形AFCE是平行四边形,又知EF垂直平分AC,所以只需证明OE=OF.
证明:∵四边形ABCD是矩形,∴AE∥FC,∴ ∠1=∠2,∵EF平分AC,∴OA=OC.又∵ ∠AOE=∠COF=90°,∴ △AOE≌△COF.∴ 四边形AFCE是菱形(对角线互相垂直的平行四边形是菱形).
1.如图所示,四边形ABCD是矩形,AE∥BD,DE∥AC,则四边形AODE是( )A.平行四边形但不是菱形 B.矩形C.菱形 D.无法确定
2.如图,剪两张对边平行且宽度相同的纸条随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( )A.∠ABC=∠ADC,∠BAD=∠BCDB.AB=BCC.AB=CD,AD=BCD.∠DAB+∠BCD=180°
3.如图所示,AE是▱ABCD的∠DAB的平分线,且交BC于点E,EF∥AB交AD于点F,则四边形ABEF一定是_______.
4.如图所示,在矩形ABCD中,E,F,G,H分别是边AB,CD,BC,DA的中点,则四边形EGFH是______形.
5.如图,在▱ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF.求证:四边形AECF是菱形.
证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∵DE=BF,∴AE=CF,∵AE∥CF,∴四边形AECF是平行四边形,∵AC⊥EF,∴平行四边形AECF是菱形
6.如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连结AF,BE.(1)求证:△AGE≌△BGF;(2)试判断四边形AFBE的形状,并说明理由.
解:(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠AEG=∠BFG,∵EF垂直平分AB,∴AG=BG,∠AGE=∠BGF,∴△AGE≌△BGF(AAS)(2)四边形AFBE是菱形,理由如下:∵△AGE≌△BGF,∴AE=BF,∵AD∥BC,∴四边形AFBE是平行四边形,又∵EF⊥AB,∴四边形AFBE是菱形
有一组邻边相等的平行四边形叫做菱形.
对角线互相垂直的平行四边形是菱形.
有四条边相等的四边形是菱形.
取两根长度不等的细纸条,将两根纸条的中点重合并固定在一起,用笔和直尺画出纸条四个端点的连线,则这四条线段组成一个什么图形,若转动其中一根纸条,使两根纸条之间的夹角等于 90° ,请猜想这时图形的形状是什么图形?
1.定义:一组邻边相等的平行四边形叫做菱形.
菱形的定义作为我们判定菱形的基本方法,接下来我们从边上来研究菱形的判定方法.
∵四边形ABCD是平行四边形,AB=AD.
∴四边形ABCD是菱形.
四条边相等的四边形是菱形.
作一个四条边都相等的四边形.步骤:1.画两条相等的线段AB、CD;2.分别以点B和点D为圆心,AB长为半径画弧,两弧相交于点C;3.连结BC、CD,即得一个四条边都相等的四边形ABCD.
命题:四条边相等的四边形是菱形.
已知:在四边形ABCD中, AB=BC=CD=DA.求证:四边形ABCD是菱形.
证明:∵AB=CD,AD=BC,∴四边形ABCD是平行四边形.又∵AB=AD,∴四边形ABCD是菱形.
定理:四条边相等的四边形是菱形.
有三条边相等的四边形是菱形吗?请同学动手画一画,你发现什么结论?
结论:有三条边相等的四边形不是菱形.
数学语言:在四边形ABCD中, ∵ AB=BC=CD=DA,∴四边形ABCD是菱形.
菱形的判定1:四条边都相等的四边形是菱形.
例4 如图,在矩形ABCD中,点E、F、G、H分别是四条边的中点,试问四边形EFGH是什么图形?并说明理由.
若四边形ABCD的对角线AC⊥BD,则四边形ABCD是不是菱形?
结论:对角线互相垂直的四边形不能判定为菱形.
对角线互相垂直的平形四边形是菱形吗?
作一个两条对角线互相垂直的平行四边形.步骤:1.作两条互相垂直的直线m,n,记交点为点O;2.以点O为圆心,适当长为半径画弧,在直线m上截取相等的两条线段OA、OC;3.以点O为圆心,另一适当长为半径画弧,在直线n上截取相等的两条线段OB、OD;4.顺次连结所行的四点,即得一个对角线互相垂直且平分的四边形ABCD,显然,它是一个对角线互相垂直的平行四边形.
这个平行四边形是菱形吗?
命题:对角线互相垂直的平行四边形是菱形.
已知:在平行四边形ABCD中,AC⊥BD .求证:平行四边形ABCD是菱形.
证明:∵四边形ABCD是平行四边形,∴OA=OC.又∵AC⊥BD,∴BA=BC, ∴ 平行四边形ABCD是菱形.(有一组邻边相等的平行四边形是菱形)
定理:对角线互相垂直的平行四边形是菱形.
数学语言:∵在□ABCD中,AC⊥BD,∴ □ABCD是菱形.
菱形的判定2:对角线互相垂直的平行四边形是菱形.
这四条线段组成平行四边形,理由:对角线互相平分的四边形是平行四边形.当两根纸条之间的夹角等于 90° 时,这时图形是菱形,理由:对角线互相垂直的平行四边形是菱形.
例5 如图,已知矩形ABCD的对角线AC的垂直平分线与边AD 、BC分别交于E、F. 求证:四边形AFCE是菱形.
分析:要证四边形AFCE是菱形,由已知条件可知EF⊥AC,所以只需证明四边形AFCE是平行四边形,又知EF垂直平分AC,所以只需证明OE=OF.
证明:∵四边形ABCD是矩形,∴AE∥FC,∴ ∠1=∠2,∵EF平分AC,∴OA=OC.又∵ ∠AOE=∠COF=90°,∴ △AOE≌△COF.∴ 四边形AFCE是菱形(对角线互相垂直的平行四边形是菱形).
1.如图所示,四边形ABCD是矩形,AE∥BD,DE∥AC,则四边形AODE是( )A.平行四边形但不是菱形 B.矩形C.菱形 D.无法确定
2.如图,剪两张对边平行且宽度相同的纸条随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( )A.∠ABC=∠ADC,∠BAD=∠BCDB.AB=BCC.AB=CD,AD=BCD.∠DAB+∠BCD=180°
3.如图所示,AE是▱ABCD的∠DAB的平分线,且交BC于点E,EF∥AB交AD于点F,则四边形ABEF一定是_______.
4.如图所示,在矩形ABCD中,E,F,G,H分别是边AB,CD,BC,DA的中点,则四边形EGFH是______形.
5.如图,在▱ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF.求证:四边形AECF是菱形.
证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∵DE=BF,∴AE=CF,∵AE∥CF,∴四边形AECF是平行四边形,∵AC⊥EF,∴平行四边形AECF是菱形
6.如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连结AF,BE.(1)求证:△AGE≌△BGF;(2)试判断四边形AFBE的形状,并说明理由.
解:(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠AEG=∠BFG,∵EF垂直平分AB,∴AG=BG,∠AGE=∠BGF,∴△AGE≌△BGF(AAS)(2)四边形AFBE是菱形,理由如下:∵△AGE≌△BGF,∴AE=BF,∵AD∥BC,∴四边形AFBE是平行四边形,又∵EF⊥AB,∴四边形AFBE是菱形
有一组邻边相等的平行四边形叫做菱形.
对角线互相垂直的平行四边形是菱形.
有四条边相等的四边形是菱形.













