数学19.3 正方形评课ppt课件

这是一份数学19.3 正方形评课ppt课件，文件包含193正方形pptx、193正方形--练习docx、193正方形--学案doc、193正方形--教案docx等4份课件配套教学资源，其中PPT共23页， 欢迎下载使用。
1.叙述平行四边形、矩形、菱形的定义和它们的特殊性质.2.说一说平行四边形、矩形、菱形的内在联系.
观察下面图形,正方形是我们熟悉的几何图形，在生活中无处不在.
你能从这个变化过程中给正方形下定义吗?
有一个角是直角的菱形叫做正方形。
有一组邻边相等的矩形叫做正方形。
有一个角是直角一组邻边相等的平行四边形叫做正方形。
由正方形的定义可知， 正方形既是有一组邻边相等的矩形，又是有一个角为直角的菱形.如图.
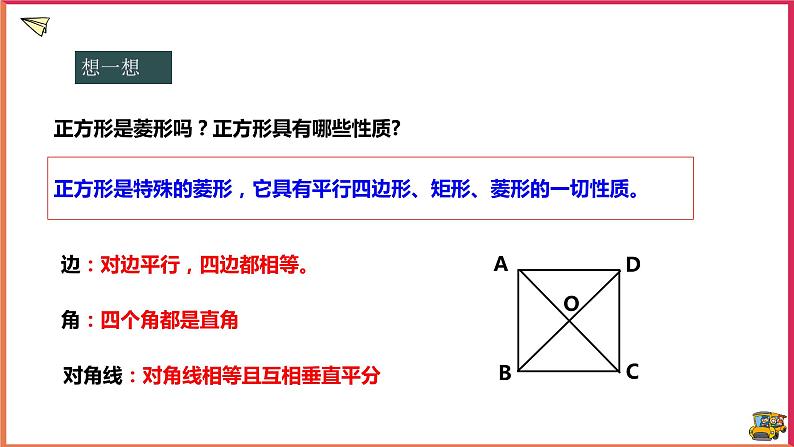
正方形是菱形吗？正方形具有哪些性质?
正方形是特殊的菱形，它具有平行四边形、矩形、菱形的一切性质。
边：对边平行，四边都相等。
对角线：对角线相等且互相垂直平分
正方形是轴对称图形吗?如果是,它有几条对称轴?
正方形是轴对称图形，它有四条对称轴.即两条对角线，两组对边的中垂线.
对称：正方形既是轴对称图形，也是中心对称图形.
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以矩形、菱形有的性质,正方形都有.
平行四边形、矩形、菱形、正方形之间关系：
性质：1.正方形的四个角都是直角,四条边相等. 2.正方形的对角线相等且互相垂直平分.
例1、如图，已知正方形ABCD，求∠ABD、∠DAC、∠DOC的度数.
已知: 如图,四边形ABCD是正方形,对角线AC、BD相交于点O.
求证: △ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.
证明: ∵ 四边形ABCD是正方形,∴ AC=BD,AC⊥BD,AO=BO=CO=DO.∴ △ABO、 △BCO、 △CDO、 △DAO都是等腰直角三角形,并且△ABO≌ △BCO ≌ △CDO ≌ △DAO.
从图中可看出，⑴在正方形中产生了哪些特殊图形？⑵产生了哪些特殊角？
4个全等的小等腰直角三角形和4个全等的大等腰直角三角形.
正方形图形“庐山真面目”
　　怎样判定一个矩形是正方形？怎样判定一个菱形是正方形？　　怎样判定一个平行四边形是正方形？　
① 对角线相等的菱形是正方形 ( )
② 对角线互相垂直的矩形是正方形 ( )
③ 对角线互相垂直且相等的四边形是正方形 ( )
④ 四条边都相等的四边形是正方形 ( )
⑤ 四个角都相等的四边形是正方形 ( )
⑥ 四边相等，有一个角是直角的四边形是正方形.( )
例、在正方形ABCD中，点E、F、M、N分别在各边上，且AE=BF=CM=DN．四边形EFMN是正方形吗?为什么?
∴△AEN≌△BFE≌△CMF≌△DNM,∴EN=FE=MF=NM，∠ANE=∠BEF,∴四边形EFMN是菱形， ∠NEF=180°－（∠AEN+∠BEF） =180°－（∠AEN+∠ANE） =180°－90°=90°.∴四边形EFMN是正方形 .
如图，在直角三角形中，∠C=90°，∠A、∠B的平分线交于点D.DE⊥AC，DF⊥AB.求证:四边形CEDF为正方形.
证明：∵ DE⊥AC，DF⊥AB ，∴∠DEC= ∠DFC=90°.又∵ ∠C=90 °，∴四边形EDFC是矩形.过点D作DG⊥AB，垂足为G.∵AD是∠CAB的平分线 DE⊥AC，DG⊥AB，∴ DE=DG. 同理得DG=DF，∴ED=DF， ∴矩形EDFC是正方形.
1、下列判断中正确的是 ( ) A．四边相等的四边形是正方形 B．四角相等的四边形是正方形 C．对角线垂直的平行四边形是正方形 D．对角线互相垂直平分且相等的四边形是正方形2、正方形具有而矩形不一定有的性质是( )A．四个角是直角 　B．对角线互相垂直C．对角线互相平分 D．对角线相等3、矩形,菱形,正方形都具有的性质是 ( ) A．邻边相等 B． 邻角相等 C．对边相等 D． 对角互补
4、在正方形ABCD中，∠ADB= ，∠DAC= ， ∠BOC= .5、在正方形ABCD中，E是对角线AC上一点，且AE=AB，则∠EBC的度数是 .
6、如图，分别延长等腰直角三角形OAB的两条直角边AO和BO，使AO=OC，BO=OD．求证：四边形ABCD是正方形．
证明：∵AO=OC，BO=OD， ∴四边形ABCD是平行四边形 ∵等腰三角形OAB中， AO⊥BO，AO=BO， ∴AO=BO=CO=DO ，AC⊥BD 即 AC=BD． ∴四边形ABCD是正方形．
7、如图，在正方形ABCD中，E为CD上一点，F为BC边延长线上一点，且CE=CF．BE与DF之间有怎样的关系？请说明理由．
解：BE=DF，且BE⊥DF．理由如下：∵四边形ABCD是正方形，∴BC=DC,∠BCE =90° ，∴∠DCF=180°-∠BCE=90°，∴∠BCE=∠DCF．又∵CE=CF，∴△BCE≌△DCF．∴BE=DF．
【浙江】如图，等边△AEF的顶点E，F在矩形ABCD的边BC，CD上，且∠CEF=45°．求证：矩形ABCD是正方形．
证明：∵四边形ABCD是矩形， ∴∠B=∠D=∠C=90 ° ， ∵△AEF是等边三角形， ∴AE=AF，∠AEF=∠AFE=60 ° ， ∵∠CEF=45 ° ， ∴∠CFE=∠CEF=45 ° ， ∴∠AFD=∠AEB=180 ° −45 ° −60 ° =75 ° ， ∴△AEB≅△AFD(AAS) ， ∴AB=AD，∴矩形ABCD是正方形．