初中数学华师大版八年级下册2.平均数、中位数和众数的选用课文配套课件ppt

这是一份初中数学华师大版八年级下册2.平均数、中位数和众数的选用课文配套课件ppt，文件包含2022平均数中位数和众数的选用ppt、2022平均数中位数和众数的选用--学案docx、2022平均数中位数和众数的选用--练习doc、2022平均数中位数和众数的选用--教案doc等4份课件配套教学资源，其中PPT共22页， 欢迎下载使用。

平均数：包含算术平均数和加权平均数：算术平均数的计算只需将总数除以数据个数即可；加权平均数的计算需考虑各部分在总体中的权重.中位数：计算中位数应先将数据按照从小到大或从大到小的顺序排列（相等的数据也要全部参与排列），则正中间的那个数字就是这组数据的中位数.如果正中间的数字有两个，则把这两个数字的算术平均数作为这组数据的中位数.众数：一组数据中出现次数最多的值.一组数据可能只有一个众数也可能有多个，但是，如果这组数据中每个值出现的次数相同，那么这组数据没有众数.
问题2：八年级某班的教室里，三位同学正在为谁的数学成绩最好而争论，他们的5次数学成绩分别是：小华：62，94，95，98，98；小明：62，62，98，99，100；小丽：40，62，85，99，99．他们都认为自己的成绩比另两位同学好，你看呢?
你认为三位同学哪位同学的成绩较好？
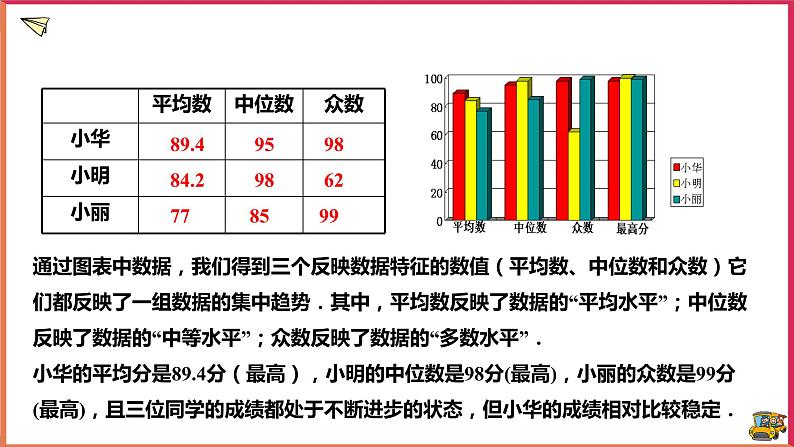
89.4 95 9884.2 98 6277 85 99
通过图表中数据，我们得到三个反映数据特征的数值（平均数、中位数和众数）它们都反映了一组数据的集中趋势．其中，平均数反映了数据的“平均水平”；中位数反映了数据的“中等水平”；众数反映了数据的“多数水平”．小华的平均分是89.4分（最高），小明的中位数是98分(最高)，小丽的众数是99分(最高)，且三位同学的成绩都处于不断进步的状态，但小华的成绩相对比较稳定．
想一想:高一级学校录取新生主要依据是考生的总分,这与平均数、中位数和众数中的哪个量关系最大?
概括:平均数较敏感,一组数据中任何一个数据的变化都会引起平均数发生变化,有时变化很明显.所以评价成绩一般用平均数.
问题3：随着汽车的日益普及，越来越多的城市发生了令人头痛的交通堵塞问题．你认为用过往车辆一天车速的平均数衡量某条交通主干道的路况合适吗？
分析：人们上、下班两个时段是一天中道路最繁忙的时候，其它时段车流量明显减少，因此，如果用一天车速的平均数来衡量道路的路况，那么上、下班交通堵塞的问题就给掩盖了．所以，应该按道路繁忙的不同程度，将一天分为几个时段分别计算车速较为合理．
平均数、中位数和众数各有其长，也各有其短，看看下面这些例子，和同学交流一下，应如何合理选用各种指标．
（1）草地上有6个人正在玩游戏，他们年龄的平均数是15岁．请想象一下是怎样年龄的6个人在玩游戏．
通常人们会想象是一群中学生在玩游戏．但是，如果是一个65岁的大娘领着5个5岁的孩子在玩游戏也是有可能的．这是一个不适合用平均数而适合用众数或中位数代表一组数据的例子，大娘的年龄把平均年龄一下子抬上去了．
（2）某商场一天中售出运动鞋20双，其中各种号码的鞋的销售如下：请你推测一下，如果你是鞋厂经理，在平均数、中位数、众数中你最关心哪个数据？最不关心的是哪个数据?
最关心的数据为众数，因为它表明工厂应该多生产这一鞋号的鞋．最不关心的数据为平均数，因为有可能没有一个顾客的鞋号等于这个平均数．
在不同的事件中,平均数,中位数和众数所起的作用不同．要反映一组数据的“多数水平”,一般选用众数．
（3）八年级有4个班级，如果已知在一次测验中这4个班级每班学生成绩的平均分，也知道各班级的学生人数，你能计算出整个年级学生的平均分吗？如何计算？如果已知的是每个班级学生成绩的中位数或者众数，那么你能得出整个年级学生成绩的中位数或者众数吗？
能计算出整个年级学生的平均分．如果已知的是每个班级学生成绩的中位数或者众数，不能得出整个年级学生成绩的中位数或者众数．
平均数、中位数和众数都是刻画一组数据集中趋势的方法，因为方法不同，所以得到的结论也可能不同． 不同的方法没有对错之分，能够更客观地反映实际背景的方法更好一些．平均数应用最广泛，它是一组数据的一个较好的代表值．在数据分析数据时，应根据不同情况合理选用平均数、中位数或众数．当一组数据中出现极端值时，会导致平均数偏大（或偏小），因此用中位数或众数要比用平均数更客观一些． 中位数的优点是计算简单，只与其在数据中的位置有关，但不能充分利用所有的信息，当一组数据中个别数据偏差较大时，可用中位数来描述这组数据的集中趋势。 众数只与其在数据中重复的次数有关，而且往往不是唯一的，当一组数据中有不少数据重复出现时，可以选择众数进行描述。
例 某公司33名职工的月工资（单位：元）如下：
（1）求该公司职工月工资的平均数、中位数和众数（精确到个位）；
（2）假设副董事长的工作从5000元提升到20000元，董事长的工资从5500元提升到30000元，那么新的平均数、中位数、众数又各是多少？（精确到个位）
（3）你认为哪个统计量更能反映这个公司职工的工资水平并说明理由．
平均数：2091元，中位数是1500元，众数是1500元；
平均数：3288元，中位数是1500元，众数是1500元；
中位数和众数更能反映这个公司职员的工资水平．
则这些队员投中次数的众数、中位数和平均数分别为(　　)A．5，6，6 B．2，6，6 C．5，5，6 D．5，6，5
1．某校男子篮球队10名队员进行定点投篮练习，每人投篮10次，他们投中的次数统计如下表：
A．参加本次植树活动的共有30人B．每人植树量的众数是4棵C．每人植树量的中位数是5棵D．每人植树量的平均数是5棵
2．某单位组织职工开展植树活动，植树量与人数之间的关系如图，下列说法不正确的是(　　)
3．在庆祝中华人民共和国成立70周年的校园歌唱比赛中，11名参赛同学的成绩各不相同，按照成绩取前5名进入决赛．如果小明知道了自己的比赛成绩，要判断能否进入决赛，小明需要知道这11名同学成绩的(　　) A．平均数 B．中位数 C．众数 D．加权平均数
4．在一次体检中，甲、乙、丙、丁四位同学的平均身高为1.65米，而甲、乙、丙三位同学的平均身高为1.63米，下列说法一定正确的是(　　) A．四位同学身高的中位数一定是其中一位同学的身高 B．丁同学的身高一定高于其他三位同学的身高 C．丁同学的身高为1.71米 D．四位同学身高的众数一定是1.65米
5．某公司33名职工的月工资(以元为单位)如下表：
(1)求该公司职工月工资的平均数、中位数、众数．(结果精确到1元)
(2)假设副董事长的月工资从5 000元提升到20 000元，董事长的月工资从 5 500元提升到30 000元，那么新的平均数、中位数、众数又是多少？ (结果精确到1元)
(3)你认为应该使用平均数和中位数中哪一个来描述该公司职工的月工资水平？
1．平均数、中位数和众数的概念，和它们各自的特点．2．结合具体情况体会平均数、中位数、众数三者的差别，能初步选择恰当的数据作出自己的判断．