数学六年级下册6 整理与复习4 数学思考复习ppt课件

这是一份数学六年级下册6 整理与复习4 数学思考复习ppt课件，共60页。PPT课件主要包含了找规律解决实际问题，整理和复习，谢谢观赏，列表法解决实际问题，等量代换解决实际问题，练习二十二等内容，欢迎下载使用。

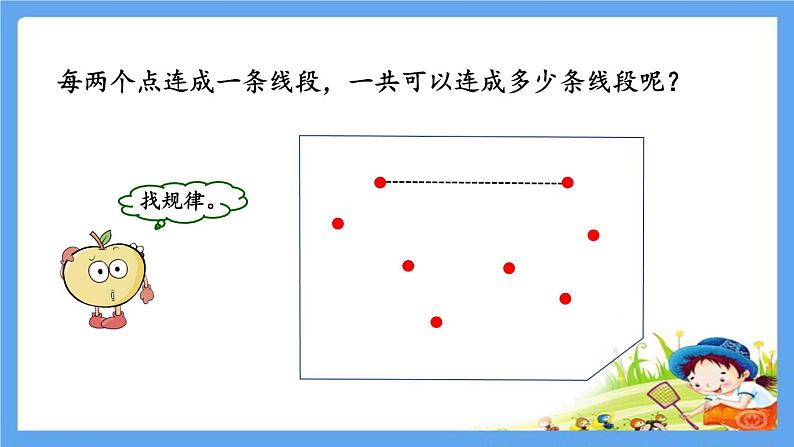
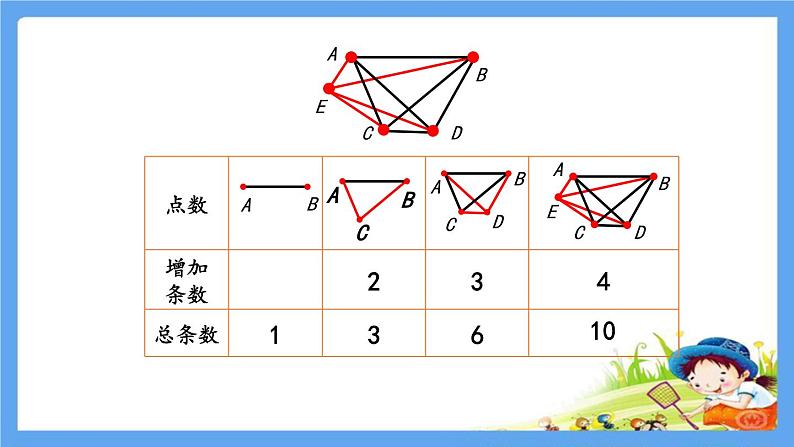
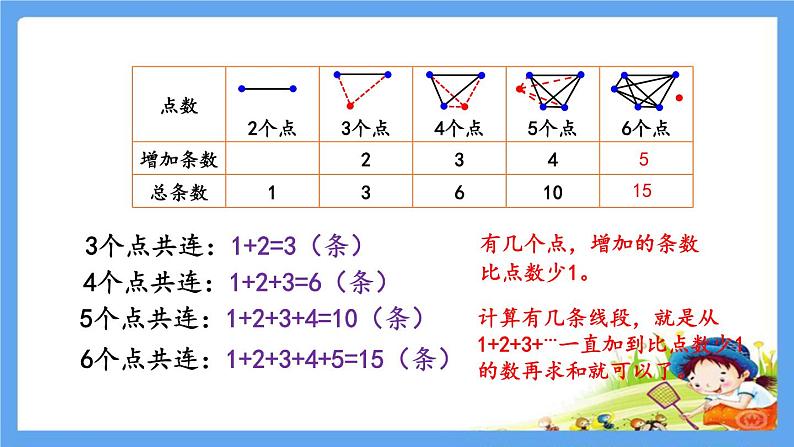
每两个点连成一条线段，一共可以连成多少条线段呢？
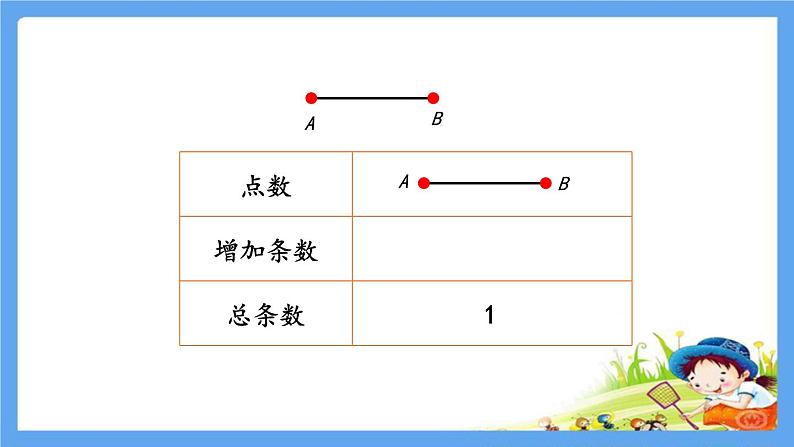
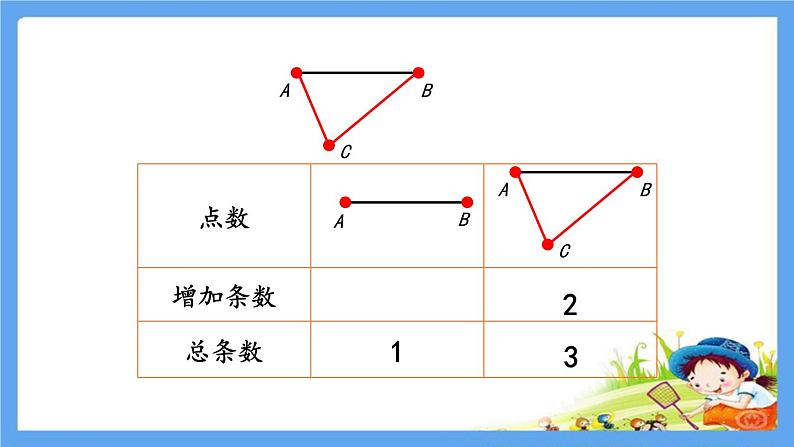
3个点共连：1+2=3（条）
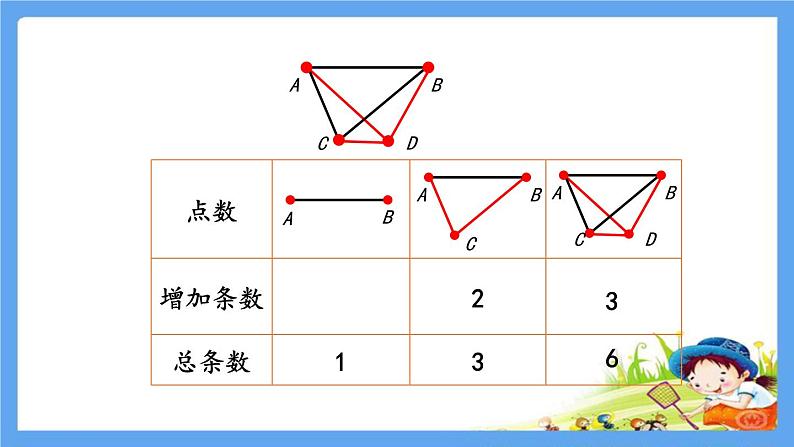
4个点共连：1+2+3=6（条）
5个点共连：1+2+3+4=10（条）
6个点共连：1+2+3+4+5=15（条）
有几个点，增加的条数比点数少1。
计算有几条线段，就是从1+2+3+…一直加到比点数少1的数再求和就可以了。
根据规律，你知道12个点、20个点能连成多少条线段？请写出算式。
(1)第7幅图有多少个棋子？第15幅图呢？
1 4 9 16
7×7＝49（个）
15×15＝225（个）
答：第7幅图有49个棋子，第15幅图有225个棋子。
(2) 每边的棋子数与图形的序号有什么关系？
答：每边的棋子数与图形的序号相等。
(3)第n幅图每边有多少个棋子？一共有多少个棋子？
每行的棋子数×行数＝棋子总数
n2＝棋子总数
答：第n幅图每边有n个棋子，一共有n2个棋子。
找一找规律，在括号里填上适当的数。
9，11，15，21，29，（ ），（ ）。
1，2，3，1，2，6，1，2，12，（    ），（    ），（    ）。
观察下面一组算式，再填出适当的数。
（1） 1×9＋2=11
（2） 12×9＋3=111
（3） 123×9＋4=1111
得数都是由数字1组成的；
第二个加数是几，得数就由几个1组成。
第一个加数是从1开始的自然数按照从小到大的顺序排列的，它的位数比后面的加数少1。
（4） 1234×9＋5=（ ）
（5） 12345×9＋（ ）=111111
（6） （ ）×9＋（ ）=11111111
根据下表中的排列规律，在空格里填上适当的数。
，下面第一个数是上面两个数的和。
下面第二个数是上面第二个数与下面第一个数的乘积。
观察点阵中的规律，画出下一个图形。
课堂感想1、这节课你有什么收获？2、这节课还有什么疑惑？说出来和大家一起交流吧！
六年级有三个班，每班有2个班长。开班长会时，每次每班只要一个班长参加。第一次到会的有A、B、C；第二次有B、D、E；第三次有A、E、F。请问：哪两位班长是同班的？
用数字“1”表示到会
用数字“0”表示没到会
有且只有一个班长参加。
第一次：A只可能和D、E、F同班。
第二次：A只可能和D、E同班。
第三次：A只可能和D同班。
A和D同班，则B只可能和E、F同班，根据第二轮推测，B和F同班，据此可推出C、E同班。
请问：他们的职业各是什么？
王阿姨、刘阿姨、丁叔叔、李叔叔分别是工人、教师、军人。王阿姨是教师；丁叔叔不是工人；只有刘阿姨和李叔叔的职业相同。
答：王阿姨是教师，丁叔叔是军人，刘阿姨和李叔叔都是工人。
学校组织了足球，航模和电脑兴趣小组，淘气、笑笑和小明分别参加了其中一项。笑笑不喜欢踢足球，小明没有参加电脑小组，淘气喜欢航模。他们分别在哪个小组。
答：淘气在航模小组， 笑笑在电脑小组，小明在足球小组。
球场休息时，保管员慌忙中把甲、乙、丙三个运动员先前交给他的水瓶都递送错了，结果甲喝的是丙的。乙、丙各喝的是谁的？
答：乙喝的是甲的，丙喝的是乙的。
下图中一共有几条线段？
或7×（7-1）÷2=21（条）
（7-1）+5+4+3+2+1=21（条 ）
小明、小莉、小刚、小芳四个好朋友站成一排拍毕业纪念照，要求男女间隔排列，一共有多少种站法？
（5）小莉 小明 小芳 小刚（6）小莉 小刚 小芳 小明（7）小芳 小明 小莉 小刚（8）小芳 小刚 小莉 小明
（1）小明 小莉 小刚 小芳（2）小明 小芳 小刚 小莉（3）小刚 小莉 小明 小芳（4）小刚 小芳 小明 小莉
答：共有8种不同的站法。
B1 B2
小明 小刚 小莉 小芳
A1 A2 B1 B2
第一位 第二位 第三位 第四位 A1 A2
当它们变成数字时又会发生什么有趣的事呢，一起来看看！
什么是平角？平角与直线有什么区别？
一条射线绕它的端点旋转，当始边和终边在同一条直线上，方向相反时，所构成的角叫平角。
如右图，两条直线相交于点O。
(1)每相邻两个角可以组成一个平角，一共能组成几个平角？
平角的两边在一条直线上，
∠1和∠2， ∠ 2和∠3，∠3和∠4，∠4和∠1，一共能组成4个平角。
(2)你能推出∠1＝∠3吗？
∠1+∠2=180°， ∠2+∠3=180° ，
等式的两边同时减去∠2，可以得到：
∠1=180°-∠2，∠3=180°-∠2，
因为180°-∠2=180°-∠2，所以∠1=∠3。
（2）○+□=31△+○=20 □+△=39 ○=（ ） △=（ ） □=（ ）
（1）○+△=150○= 4×△ ○=（ ） △=（ ）
下面算式中 、 各代表一个数。
+ =10， + =12， + + =15。
求 、 、 的值。
如图中∠1=30°，∠2=50°，求∠3、∠4、∠5的度数。
因为∠1+∠5=180° ， ∠1=30°
所以∠5=180° -∠1 =180° -30° =150°
因为∠4+∠5=180°， ∠5=150°
所以∠4=180° -∠5 =180° -150° =30°
因为∠3+∠2+∠4=180°， ∠4=30° ，∠2=50°
所以∠3=180° -∠4-∠2 =180° -30°-50° =100°
数学思想和方法可以帮助我们有条理地思考，简捷地解决问题。
生活中的一些推理问题比较复杂，可以借助表格帮助我们推理，从而解决问题。
等量代换是指一个量用与它相等的量去代替，它是数学中一种基本的思想方法。
（1）第6个图形是什么图形？
（2）摆第7个图形需要用多少根小棒？
1+2×7=15（根）
（3）摆第n个图形需要用多少根小棒？
答：摆第7个图形需要用15根小棒。
答：摆第n个图形需要用1+2n根小棒。
（1）多边形内角和与它的边数有什么关系？
多边形里分成的三角形个数，正好是这个多边形的边数-2。
多边形内角和＝（边数－2）×180°
（2）一个九边形的内角和是多少度？
（3）一个n的内角和是多少度？
（9－2）×180°＝1260°
（n－2）×180°
张老师有50分和80分的邮票各两枚。他用这些邮票能付多少种邮资？
1枚：50分、80分。有2种
2枚：100分、130分、160分。 有3种。
3枚：180分、210分。有2种
4枚：260分。有1种
警察抓住了4个偷东西的嫌疑人，其中的一个是主谋。审问谁是主谋时，甲说：我不是主谋。乙说：丁是主谋。丙说：我不是主谋。丁说：甲是主谋。已知他们4人中只有一个人说了真话。主谋是谁？
乙说的就是假的，那么丁就不是主谋；丙说的是假的，丙是主谋；丁说的是假的，甲不是主谋。
推理时，可先找出矛盾的两句话，因只有一人是真话，那么这两句话中必有一句是假的。所以可假设其中一句是真的，然后再推理。
学校为艺术节选送节目，从3个合唱节目中选出2个，2个舞蹈节目中选出1个，一共有几种选送方案？
第三步：把两次选法进行搭配，共有6种选法。
第一步：从3个合唱节目中选出2个，有3种选法。
第二步：从2个舞蹈节目中选出1个，有2种选法。
答：一共有6种选送方案。
如果用A、B、C表示3个合唱节目，用a、b表示2个舞蹈节目。
如图，把三角形ABC的边BC延长到点D。（1）∠3和∠4拼成的是什么角？（2）你能说∠1+∠2=∠4吗？
（1）∠3和∠4拼成的是平角。
（2）因为∠1+∠2+∠3=180°
所以∠1+∠2+∠3=∠3+∠4
两边都减去∠3，可以得到：
这节课你们都学会了哪些知识？
1.会归纳、类比、推理的思想方法，培养数学的逻辑思维。2.有序思考解决生活中实际问题。