初中数学人教版七年级下册第五章 相交线与平行线综合与测试达标测试

这是一份初中数学人教版七年级下册第五章 相交线与平行线综合与测试达标测试，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


一、选择题(本大题共8小题，每小题只有一个正确选项，每小题3分，共24分)
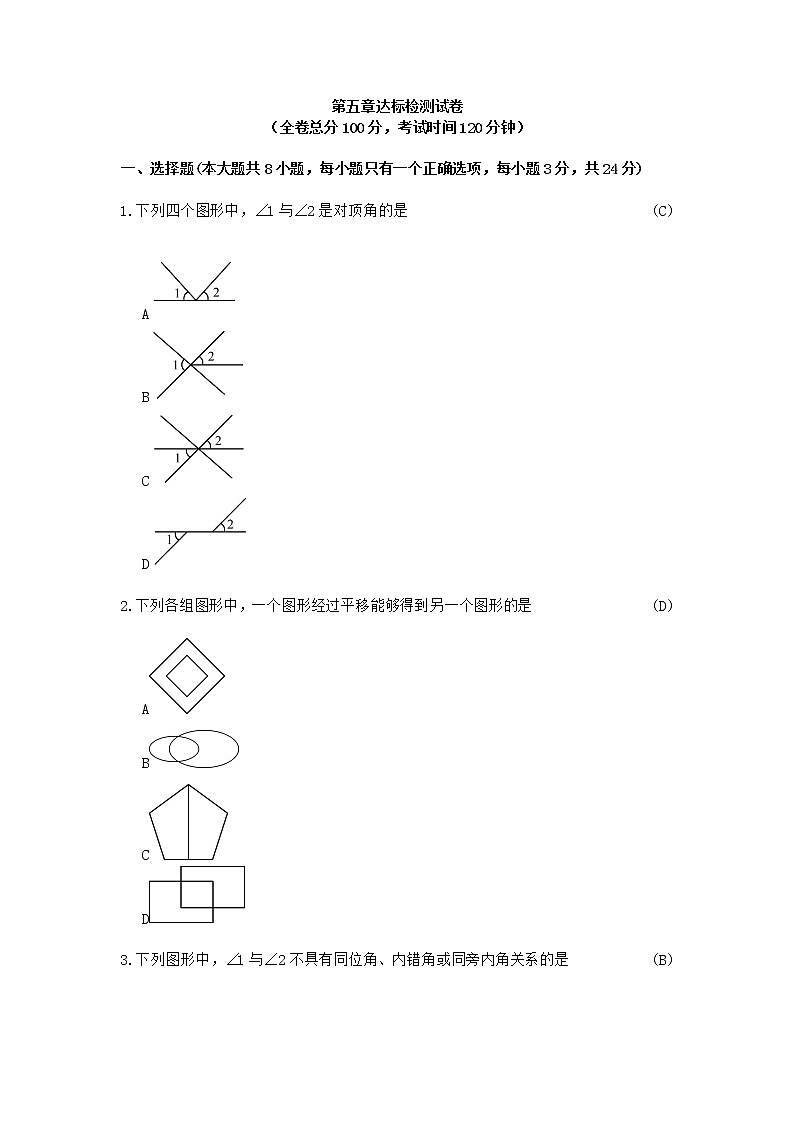
1.下列四个图形中，∠1与∠2是对顶角的是(C)
A
B
C
D
2.下列各组图形中，一个图形经过平移能够得到另一个图形的是(D)
A
B
C
D
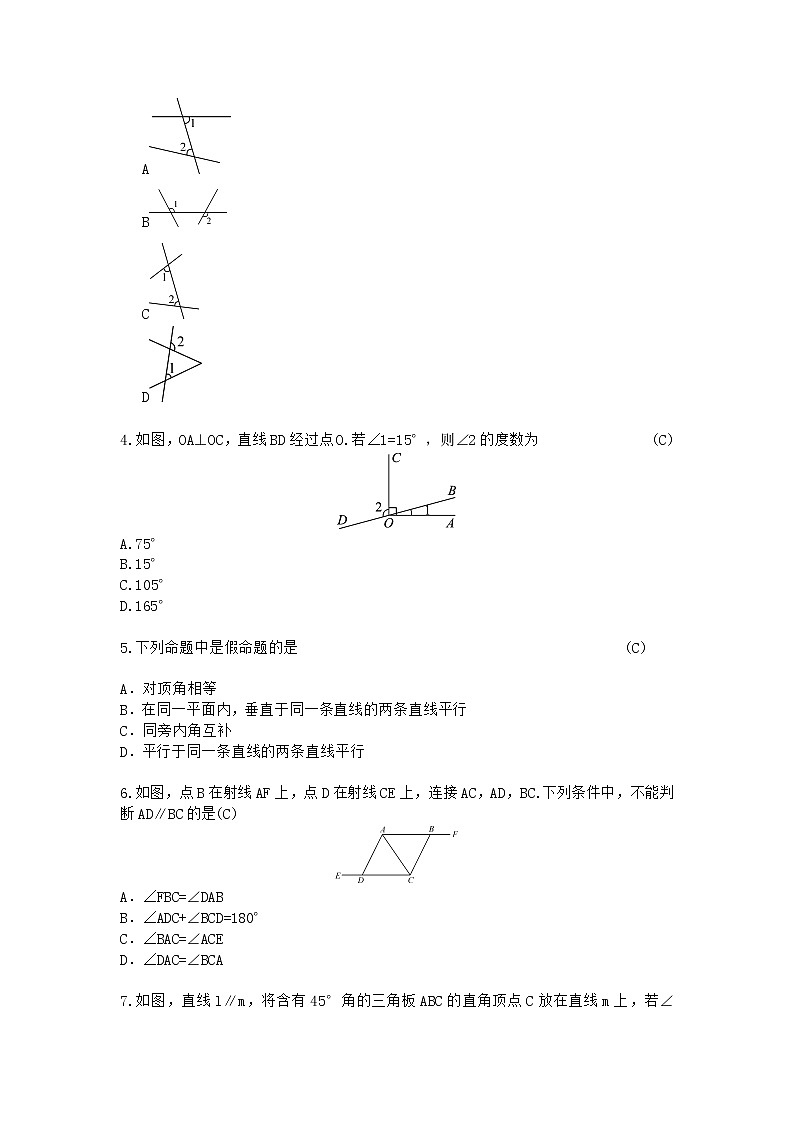
3.下列图形中，∠1与∠2不具有同位角、内错角或同旁内角关系的是(B)
A
B
C
D
4.如图，OA⊥OC，直线BD经过点O.若∠1=15°，则∠2的度数为(C)
A.75°
B.15°
C.105°
D.165°
5.下列命题中是假命题的是(C)
A．对顶角相等
B．在同一平面内，垂直于同一条直线的两条直线平行
C．同旁内角互补
D．平行于同一条直线的两条直线平行
6.如图，点B在射线AF上，点D在射线CE上，连接AC，AD，BC.下列条件中，不能判断AD∥BC的是(C)
A．∠FBC=∠DAB
B．∠ADC+∠BCD=180°
C．∠BAC=∠ACE
D．∠DAC=∠BCA
7.如图，直线l∥m，将含有45°角的三角板ABC的直角顶点C放在直线m上，若∠1=25°，则∠2的度数为(A)
A.20°B.25°C.30°D.35°
第7题图第8题图
8.如图，AD∥BC，∠B=∠D，延长BA至点E，连接CE，∠EAD和∠ECD的平分线相交于点P,AP与CE相交于点O．下列三个结论：①AB∥CD；②∠AOC=12∠EAD+∠ECD；③若∠E=60°，∠APC=70°，则∠D=80°．其中正确的个数有(D)
A．0个B．1个C．2个D．3个
二、填空题(本大题共6小题，每小题3分，共18分)
9.把命题“同旁内角互补，两直线平行”改写成“如果……那么……”的形式为如果两条直线被第三条直线所截得的同旁内角互补,那么,这两条直线平行.
10.如图，已知a∥b，∠1=70°，∠2=40°，则∠3=70 °.
0
第10题图第11题图 第12题图
11.如图，若EF∥BC，DE∥AB，∠FED=40°，则∠B=40 °.
12.如图,从书店到公路最近的是①号路线，其中应用的数学知识是垂线段最短．
13.如图，把长方形ABCD纸片沿EF折叠后，点D，C分别落在点D′，C′的位置．若∠AED′=50°，则∠EFC=115 °．
第13题图第14题图
14.两条笔直且平行的景观道AB，CD上放置了P，Q两盏激光灯（如图所示），若光线PB按顺时针方向以每秒6°的速度旋转至PA便立即回转，并不断往返旋转；光线QC按顺时针方向每秒2°的速度旋转至QD边就停止旋转.若光线QC先转5秒，光线PB才开始转动，当光线PB旋转时间为2.5或43.75秒时，PB1∥QC1．
三、解答题(本大题共9小题，共58分)
15.（本小题4分）如图，在正方形网格中有一个格点三角形ABC（即三角形ABC的各顶点都在格点上），按要求进行下列作图.
（1）画出三角形ABC中AB边上的高CD；
（2）画出将三角形ABC向上平移3格后的三角形A′B′C′.
答图
解：(1)如答图，CD为所作；
(2)如答图，三角形A ′B ′C ′为所作.
16.（本小题7分）完成推理填空:如图，在三角形ABC中，已知∠1+∠2=180°，∠3=∠B，试说明∠AED=∠C.
解：∵∠1+∠EFD=180°(邻补角定义），∠1+∠2=180°(已知),
∴∠EFD=∠2（同角的补角相等）.①
∴EF∥AB（内错角相等，两直线平行）.②
∴∠ADE=∠3(两直线平行，内错角相等).③
∵∠3=∠B(已知),④
∴∠ADE=∠B（等量代换）.⑤
∴DE∥BC(同位角相等，两直线平行).⑥
∴∠AED=∠C(两直线平行，同位角相等).⑦
17.（本小题5分）如图，点A，B，C，D在一条直线上，CE与BF相交于点G，∠A=∠1,CE∥DF.求证：∠E=∠F.
解：∵CE∥DF,∴∠ACE=∠D.
∵∠A=∠1,
∴180 °-∠ACE-∠A=180 °-∠D-∠1.
又∵∠E=180 °-∠ACE-∠A,∠F=180 °-∠D-∠1，
∴∠E=∠F.
18.（本小题5分）如图，直线AB，CD相交于点O，∠DOE=∠BOD，OF平分∠AOE．若∠AOC∶∠AOD=1∶5，求∠EOF的度数．
解：∵∠AOC∶∠AOD=1∶5，∠AOC+∠AOD=180 °，
∴∠AOC=180 °×16=30 °，∠AOD=180 °×56=150 °，
∵∠DOE=∠BOD，∠AOC=∠BOD,
∴∠AOC=∠BOD=∠DOE=30 °.
∴∠AOE=180 °-∠BOE=180 °-30 °-30 °=120 °.
∵OF平分∠AOE，
∴∠EOF=∠AOF=12∠AOE=60 °.
19. （本小题6分）如图，有以下三个条件：①AB∥CD；②∠B=∠D；③∠E=∠F．
（1）请以其中两个条件为条件，第三个条件为结论构造新的命题，并写出所有的命题；
（2）请选择（1）中的一个真命题进行证明．
解：(1)第一种：如果AB∥CD，∠B=∠D，那么∠E=∠F．
第二种：如果AB∥CD，∠E=∠F，那么∠B=∠D．
第三种：如果∠B=∠D，∠E=∠F，那么AB∥CD;
(2)证明第一种.
∵AB∥CD，∴∠B=∠DCF.
∵∠B=∠D，∴∠D=∠DCF.
∴DE∥BF.∴∠E=∠F．
20.（本小题6分）小明在C处放牛，他准备牵牛到河边饮水，请在图1中画出他所走的最短路线;如果小明先牵着牛到D处拿他放置的东西，再到河边饮水，你能在图2中画出他所走的最短路线吗？你能说明这是为什么吗？
图1图2
解：如图1，过点C作CE⊥AB，垂足为E，则小明沿着CE路线走最近.这是因为连接直线外一点与直线上各点的所有线段中，垂线段最短.
如图2，连接CD，过点D作DF⊥AB，垂足为F，则小明沿CDF路线走最近.这是因为两点之间，线段最短以及垂线段最短.
图1图2
21.（本小题8分）如图，∠1+∠2=180°，∠3=100°，OK平分∠DOH.
(1)求证：AB∥CD；
(2)求∠KOH的度数.
(1)证明：∵∠1+∠2=180 °,
∴AB∥CD；
(2)解：∵AB∥CD,
∴∠3=∠GOD.
∵∠3=100 °,
∴∠GOD=100 °.
∴∠DOH=180 °-∠GOD=80 °.
∵OK平分∠DOH，
∴∠KOH=12∠DOH=40 °.
22.（本小题8分）如图，已知∠A=∠C，AD⊥BE于点F，BC⊥BE于点B，点E，D，C在同一条直线上．
（1）判断AB与CD的位置关系，并说明理由；
（2）若∠ABC=130°，求∠BEC的度数．
解：(1)AB∥CD.理由：
∵AD⊥BE，BC⊥BE，
∴∠EFD=∠EBC=90 °.
∴AD∥BC.
∴∠ADE=∠C.
∵∠A=∠C，
∴∠ADE=∠A.
∴AB∥CD；
(2)∵∠ABC=130 °，∠EBC=90 °.
∴∠ABE=∠ABC-∠EBC=130 °-90 °=40 °.
∵AB∥CD，
∴∠BEC=∠ABE=40 °．
23.（本小题9分）如图1，直线EF与直线AB，CD分别相交于点E，F，∠1+∠2=180°．
（1）求证：AB∥CD；
（2）如图2，若M为线段EF上一定点，P是直线CD上的一个动点（点P不与点F重合）．当点P在射线FC上移动时，求证：∠FMP+∠FPM=∠AEF；
（3）如图3，当点P在射线FD上移动时，求证：∠FPM+∠AEF=∠EMP．
证明：(1)∵∠2+∠EFD=180 °，∠1+∠2=180 °，

∴∠1=∠EFD.
∴AB∥CD；
(2)如图1，过点M作MH∥AB，由(1)得AB∥CD，
∴MH∥AB∥CD.
∴∠HMF=∠AEF，∠HMP=∠FPM.
∵∠HMF=∠HMP+∠FMP，
∴∠FMP+∠FPM=∠FMP+∠HMP=∠HMF=∠AEF；
(3)如图2，过点M作MK∥AB，
由(1)得,AB∥CD，
∴MK∥AB∥CD.
∴∠EMK=∠AEF，∠KMP=∠FPM.
∵∠EMP=∠EMK+∠KMP，
∴∠FPM+∠AEF=∠KMP+∠EMK=∠EMP．