2021届重庆市名校联盟高三三模数学试题含解析

这是一份2021届重庆市名校联盟高三三模数学试题含解析，共20页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
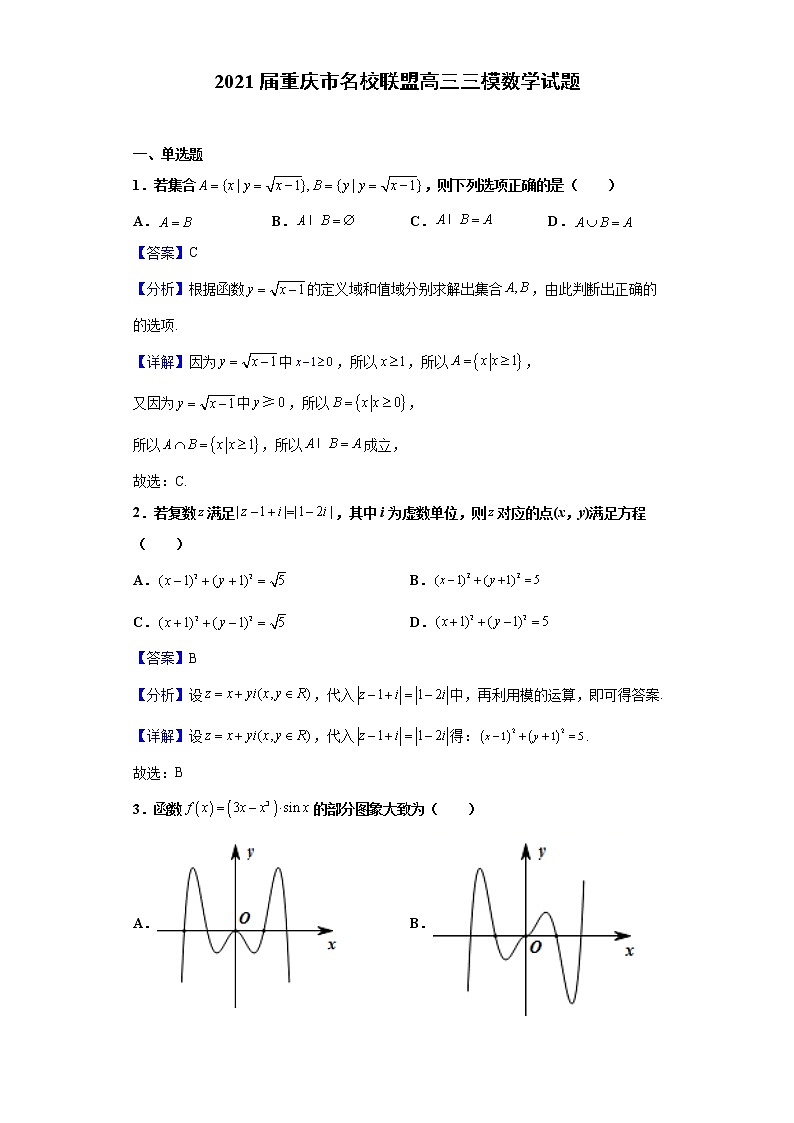
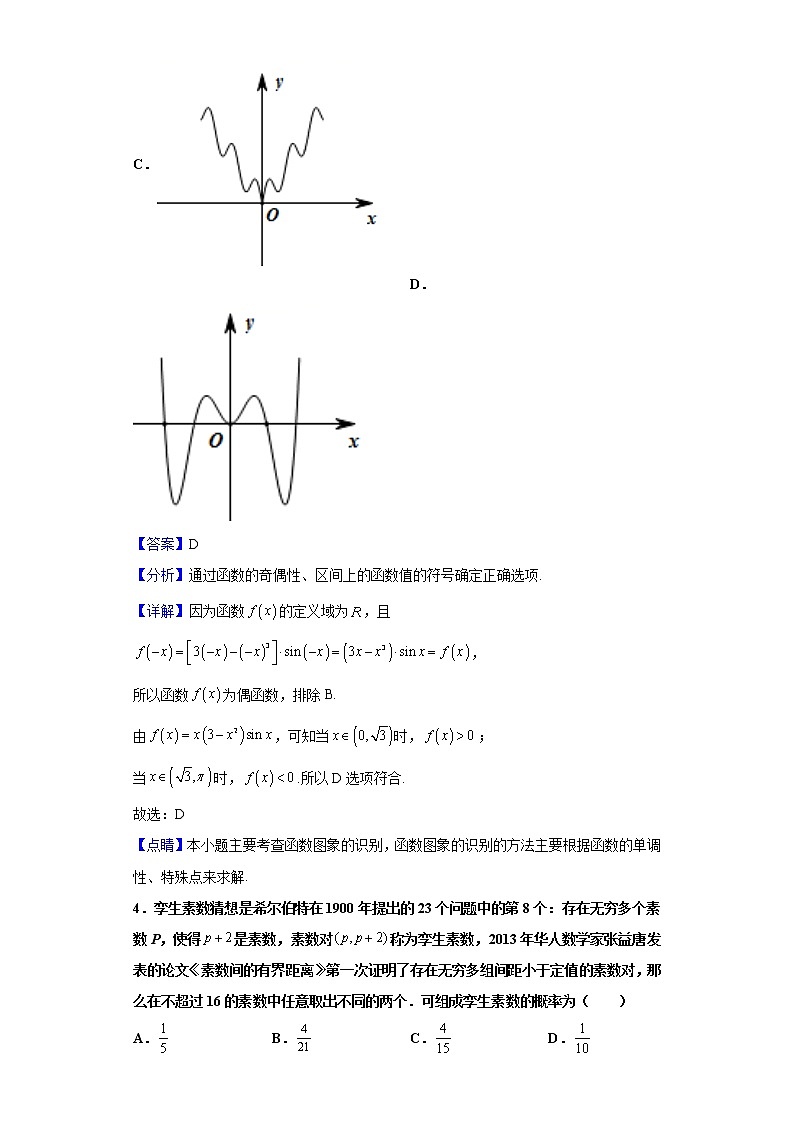
2021届重庆市名校联盟高三三模数学试题  一、单选题1．若集合，则下列选项正确的是（    ）A． B． C． D．【答案】C【分析】根据函数的定义域和值域分别求解出集合，由此判断出正确的的选项.【详解】因为中，所以，所以，又因为中，所以，所以，所以成立，故选：C.2．若复数满足，其中i为虚数单位，则对应的点(x，y)满足方程（    ）A． B．C． D．【答案】B【分析】设，代入中，再利用模的运算，即可得答案.【详解】设，代入得：. 故选：B3．函数的部分图象大致为（    ）A． B．C． D．【答案】D【分析】通过函数的奇偶性、区间上的函数值的符号确定正确选项.【详解】因为函数的定义域为，且，所以函数为偶函数，排除B.由，可知当时，；当时，.所以D选项符合.故选：D【点睛】本小题主要考查函数图象的识别，函数图象的识别的方法主要根据函数的单调性、特殊点来求解.4．孪生素数猜想是希尔伯特在1900年提出的23个问题中的第8个：存在无穷多个素数P，使得是素数，素数对称为孪生素数，2013年华人数学家张益唐发表的论文《素数间的有界距离》第一次证明了存在无穷多组间距小于定值的素数对，那么在不超过16的素数中任意取出不同的两个．可组成孪生素数的概率为（    ）A． B． C． D．【答案】A【分析】先列出不超过16以内的素数，然后利用列举法写出在这些素数中任取两个构成素数对的所有可能情况，得出为孪生素数的个数，然后计算其概率.【详解】不超过16的素数有，，，，，，共个，任取两个构成素数对，则有：，，，，，，，，，，，，，，，共中取法，而是孪生素数的有，，，这三种取法，所以其概率为.故选：A.【点睛】方法点睛：本题考查古典概型及概率计算，一般可采用列举法、列表法或树状图法求解.5．已知的展开式中各项系数之和为0，则该展开式的常数项是（    ）A． B． C．9 D．10【答案】C【分析】根据的展开式中各项系数之和为0，令可得参数，再根据通项公式可求解.【详解】的展开式中各项系数之和为0.令得，解得..则展开式的通项公式为：则展开式的常数满足：则或，则该展开式的常数项是.故选：C.6．我国古代著名的数学专著《九章算术》有一段叙述：今有良马与驽马发长安至齐，行程一千一百二十五里，良马初日行一百零三里，日减半里；驽马初日行九十七里，日减半里，良马先至齐，复还迎驽马，则二马（    ）日后相逢．A．10 B．11 C．12 D．13【答案】C【分析】根据题意通过已知条件转化为两个等差数列的前n项和为定值问题，进而计算可得结论．【详解】由题可知，良马每日行程构成一个首项为103，公差的等差数列，驽马每日行程构成一个首项为97，公差为的等差数列，则，，则数列与数列的前n项和为，又数列的前n项和为，数列的前n项和为，，整理得：，当时，，当时，，所以大12日相逢．故选:C．7．己知双曲线的左右焦点为，虚轴长为，若其渐近线上横坐标为1的点P恰好满足，则双曲线的离心率为（    ）A．2 B． C．4 D．【答案】A【分析】先求得的值，利用一条渐近线方程求得点坐标，然后利用数量积得，结合求得离心率.【详解】解：虚轴长为，得，设一条渐近线，则，，又，解得，故，故选：A.8．若关于的不等式对一切正实数恒成立，则实数的取值范围是（    ）A． B． C． D．【答案】C【分析】构造函数，将原不等式转化为求解函数的最小值，通过导数判断函数的单调性研究函数的最值，得到，再利用基本不等式进行求解即可．【详解】解：设，则对一切正实数恒成立，即，由，令，则恒成立，所以在上为增函数，当时，，当时，，则在上，存在使得，当时，，当时，，故函数在上单调递减，在，上单调递增，所以函数在处取得最小值为，因为，即，所以恒成立，即，又，当且仅当，即时取等号，故，所以．故选：C．【点睛】方法点睛：不等式恒成立问题常见方法：① 分离参数恒成立(即可)或恒成立（即可）；② 数形结合( 图象在 上方即可)；③ 讨论最值或恒成立；④ 讨论参数. 二、多选题9．空气质量指数大小分为五级，指数越大说明污染的情况越严重，对人体危窖越大，指数范围在；对应“优”､“良”､“轻度污块"､“中度污染”､“重度污染”五个等级，下面是某市连续14天的空气质量指数变化趋势图，下列说法中正确的是（    ）A．从2日到5日空气质量越来越好B．这14天中空气质量指数的极差为195C．这14天中空气质量指数的中位数是103.5D．这14天中空气质量指数为“良”的频率为【答案】BC【分析】观察折线图，可知ABD的正误，把每天的空气指数从低到高排列，计算中位数，可判断C选项.【详解】从2日到5日空气质量指数越来越高，故空气质量越来越差，故A不对；这14天中空气质量指数的极差为，故B正确；14天空气质量指数由小到大排列，中间为86，121，故中位数为：，故C正确；14天中有：1日，3日，12日，13日空气质量指数为良，共4天，所以空气质量指数为“良”的频率为，故D不对；故选： BC10．定义在实数集的函数的图象的一个最高点为，与之相邻的一个对称中心为，将的图象向右平移个单位长度得到函数的图象，则（    ）A．的振幅为B．的频率为C．的单调递增区间为D．在上只有一个零点【答案】AD【分析】先根据余弦函数的图象和性质，求得的解析式，再结合三角函数的图象变换，求得函数的解析式，再结合余弦函数的图象与性质，即可求解.【详解】由题意，可得，所以，可得，所以，所以函数的振幅为3，故A正确；函数的频率为，故B错误；因为，所以，因为，所以，即，所以，令，可得，所以的单调递增区间为，而选项C只是其中一个单调递增区间，故C错误；由，解得，所以函数在上只有一个零点.故选：AD【点睛】关键点睛：本题主要考查了三角函数的图象变换，以及三角函数的图象与性质，其中解答中熟记三角函数的图象变换，以及熟练应用三角函数的图象与性质是解答的关键.11．是定义在上周期为4的函数，且，则下列说法中正确的是（    ）A．的值域为B．当时，C．图象的对称轴为直线D．方程恰有5个实数解【答案】ABD【分析】画出的部分图象结合图形分析每一个选项即可.【详解】根据周期性，画出的部分图象如下图所示，由图可知，选项A，D正确，C不正确；根据周期为，当时，，故B正确.故选：ABD.12．如图，矩形ABCD中，M为BC的中点，将沿直线AM翻折成，连结，N为的中点，则在翻折过程中，下列说法中所有正确的是（    ）A．存在某个位置，使得B．翻折过程中，CN的长是定值C．若，则D．若，当三棱锥的体积最大时，三棱锥的外接球的表面积是4π【答案】BD【分析】取AD中点E，连接EC交MD与F，根据EN⊥CN可判断A；由∠NEC＝∠MAB1（定值），结合余弦定理可判断B；取AM中点O，连接B1O，DO，由线面垂直的性质可得OD⊥AM，即AD＝MD，进而判断C；由题意得AD中点是三棱锥B1﹣AMD的外接球的球心时，体积最大，即求.【详解】解：对于A：如图1，取AD中点E，连接EC交MD与F，则NEAB1，NFMB1，如果CN⊥AB1，可得到EN⊥NF，又EN⊥CN，且三线NE，NF，NC共面共点，不可能，故A错误．对于B：如图1，可得由∠NEC＝∠MAB1（定值），（定值），（定值），由余弦定理可得，∴NC是定值，故B正确．对于C：如图2，取AM中点O，连接B1O，DO，由题意得AM⊥面ODB1，即可得OD⊥AM，从而AD＝MD，由题意不成立，可得C错误．对于D：当平面B1AM⊥平面AMD时，三棱锥B1﹣AMD的体积最大，由题意得AD中点就是三棱锥B1﹣AMD的外接球的球心，球半径为1，表面积是4π，故D正确．故选：BD．  三、填空题13．已知，则的值是__________．【答案】【详解】∵，∴而故答案为点睛：1．利用sin2＋cos2＝1可以实现角的正弦、余弦的互化，利用＝tan可以实现角的弦切互化．2．应用公式时注意方程思想的应用：对于sin＋cos，sincos，sin－cos这三个式子，利用(sin±cos)2＝1±2sincos，可以知一求二．3．注意公式逆用及变形应用：1＝sin2＋cos2，sin2＝1－cos2，cos2＝1－sin2.14．已知，且满足，则的最小值为__________.【答案】4【分析】由指数的运算得出，再由结合二次函数的性质得出最值.【详解】由可得，即故答案为：15．已知抛物线C：的焦点为F，点M(x0，2),()是抛物线C上一点，以点M为圆心的圆与直线x＝交于E，G两点，若sin∠MFG＝，则抛物线C的方程是______.【答案】y2=4x【分析】根据点在抛物线上和，列方程组可解得和，即可得出抛物线的方程.【详解】如下图所示，作，垂足为由题意知点M(x0，2),()是抛物线C上一点，则①，由抛物线的定义，可知，因为，所以，，所以，解得②，由①②解得（舍去）或，故抛物线的方程为．故答案为：.【点睛】本题考查抛物线的定义，利用抛物线的定义进行线段的转化是关键，考查方程思想的应用，属于中档题.16．在三棱锥中，，二面角的大小为，在侧面内(含边界)有一动点，满足到的距离与到平面的距离相等，则动点的轨迹的长度为__________．【答案】【分析】如图，先作出二面角的平面角，进而得到，再建立如图所示的平面直角坐标系，可得直线的方程为，从而求出的轨迹的长度．【详解】解：如图，过作 于，平面于，过作于，连接，则为二面角的平面角，由，得．又，所以，在 中，以 所在直线为轴，所在直线为轴建立平面直角坐标系，则直线的方程为，直线的方程为，所以直线与的交点坐标为，所以的轨迹为线段，长度为．故答案为：．【点睛】关键点点睛：本题关键为利用二面角得出结论后建立平面直角坐标系求解，方法比较少见，利用直角坐标系求得直线的方程后顺利求得直线与的交点坐标，将问题转化为求线段得长度，问题解决. 四、解答题17．在①，②，③，这三个条件中任选一个，补充在下面的问题中，并解决该问题.已知的内角A，B，C的对边分别为a，b，c，_________，，.（1）求角B；（2）求的面积.【答案】（1）；（2）.【分析】（1）选①，直接利用余弦定理即可求解，选②，利用正弦定理可得求解即可，选③，利用辅助角公式化简求解即可；（2）由正弦定理求出，直接利用三角形面积公式求解.【详解】若选择①，（1）由余弦定理，因为，所以.（2）由正弦定理得，因为，所以，所以，所以.若选择②.（1）由正弦定理得，因为，所以，因为，所以；（2）由正弦定理得，因为，所以，所以，所以.若选择③，（1）由和角公式得，所以.因为，所以，所以，所以；（2）由正弦定理得，因为，所以，所以，所以.【点睛】本题主要考查了正弦定理，余弦定理，三角形面积公式，三角恒等变换，考查了推理运算能力，属于中档题.18．已知数列的前项和为，且满足．（1）求数列的通项公式：（2）设，数列的前项和为，求证：．【答案】（1）；（2）证明见解析．【分析】（1）利用，求得数列的通项公式.（2）求得数列的通项公式，进而利用裂项求和法求得，结合数列的单调性证得.【详解】（1）解：，令，解得时，两式相减，得数列是以为首项，为公比的等比数列，所以；（2）证明单调递增，所以1即19．如图，四棱锥中，，，.（1）求证：平面；（2）若，且，平面平面，，求直线与平面所成的角.【答案】（1）证明见解析；（2）.【分析】（1）取线段的靠近的三等分点为，连接，，则，所以且，再结合已知可证得四边形为平行四边形，从而有，然后利用线面平行的判定定理可证得结论；（2）取中点为，连接，过作交于，可证得直线，，两两垂直，所以以为原点，分别以射线，，的方向为，，轴的正方向建立如图所示的空间直角坐标系，然后利用空间向量求直线与平面所成的角.【详解】（1）如图，取线段的靠近的三等分点为，连接，.则，所以且.又且,所以四边形为平行四边形.所以.又平面，平面，所以平面.（2）如图，取中点为，连接，过作交于.因为平面平面，，由面面垂直的性质定理可知，平面.所以直线，，两两垂直，以为原点，分别以射线，，的方向为，，轴的正方向建立如图所示的空间直角坐标系.则，，，.所以，，.设平面的法向量为，则取，得.所以，所以直线与平面所成的角为45°.【点睛】此题考查了线面平行的证明，求直线与平面所成的角，考查了空间想象能力和计算能力，属于中档题.20．近年来，国资委.党委高度重视扶贫开发工作，坚决贯彻落实中央扶贫工作重大决策部署，在各个贫困县全力推进定点扶贫各项工作，取得了积极成效，某贫困县为了响应国家精准扶贫的号召，特地承包了一块土地，已知土地的使用面积以及相应的管理时间的关系如下表所示：土地使用面积（单位：亩）管理时间（单位：月）  并调查了某村名村民参与管理的意愿，得到的部分数据如下表所示： 愿意参与管理不愿意参与管理男性村民女性村民   求出相关系数的大小，并判断管理时间与土地使用面积是否线性相关？若以该村的村民的性别与参与管理意愿的情况估计贫困县的情况，则从该贫困县中任取人，记取到不愿意参与管理的男性村民的人数为，求的分布列及数学期望.参考公式：，参考数据：，，【答案】，管理时间与土地使用面积线性相关；分布列见解析，.【分析】，，故，，，进而求出，即可得出结论；的可能取值为，，，，从该贫困县中随机抽取一名，则取到不愿意参与管理的男性村民的概率为，由此能求出的分布列及数学期望.【详解】解：依题意：，故，则，故管理时间与土地使用面积线性相关.依题意，的可能取值为，，，，从该贫困县中随机抽取一名，则取到不愿意参与管理的男性村民的概率为，故，，，.故的分布列为 则数学期望为（或由，得）【点睛】本题考查相关系数的求法，考查分布列，数学期望的求法，考查二项分布等知识，属于中档题.21．设椭圆的离心率，焦距为4．（1）求椭圆的标准方程；（2）过椭圆右焦点的动直线交椭圆于两点，为直线上的一点，是否存在直线与点P，使得恰好为等边三角形，若存在求出的面积，若不存在说明理由．【答案】（1）；（2）存在；．【分析】（1）根据条件列式，利用待定系数法求椭圆的标准方程；（2）首先设直线，与椭圆方程联立，利用根与系数的关系表示弦长，以及中点的坐标，利用，求解直线的斜率，即可判断.【详解】解（1）；依题意，又所以：椭圆的标准方程为（2）设直线，联立椭圆方程整理得记则所以记AB中点为，则要满足题目要求，则需要，即所以，经检验均符合愿意．22．设（1）恒成立，求实数的取值范围；（2）求证：当时，．【答案】（1）；（2）证明见解析．【分析】（1）恒成立，等价于，故通过求导分析单调性求取最小值即可求得结果；（2）原不等式等价于，求导分析单调性只要证明即可．【详解】（1）解当时，恒成立，所以在为增函数､此时恒成立：当时，存在，使得，所以在单调递减，当时，与矛盾．综上所述，的取值范围为；（2）证明：原不等式等价于易知，令，则，，所以在是减函数，考虑到在也是减函数，所以，在为增函数，又因为，所以时，所以在为增函数，又因为，所以在成立，命题获证．