高中数学北师大版 必修第二册第五章 ——3.1复数的三角表示式 3.2复数乘除运算的几何意义【课件

这是一份高中数学北师大版 必修第二册第五章 ——3.1复数的三角表示式 3.2复数乘除运算的几何意义【课件

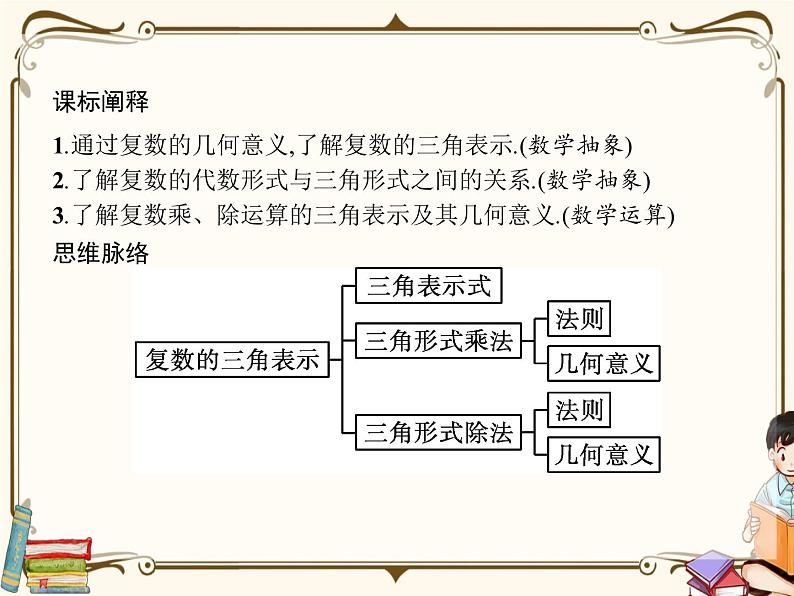
3.1　复数的三角表示式3.2　复数乘除运算的几何意义课标阐释 1.通过复数的几何意义,了解复数的三角表示.(数学抽象)2.了解复数的代数形式与三角形式之间的关系.(数学抽象)3.了解复数乘、除运算的三角表示及其几何意义.(数学运算)思维脉络 激趣诱思知识点拨建筑表皮设计是地产黄金十年期间的热门领域.在众多新建筑和国际设计竞赛中,建筑表皮设计或是成为建筑方案的特点之一,或是成为建筑师的创意核心.建筑表皮设计古已有之,并不是近年涌现的新生事物.从古代宗教建筑的立面装饰处理到密斯设计的玻璃幕墙立面都属于建筑表皮设计.20世纪后半叶,现代建筑的一元化局面遭遇挑战,建筑表皮开始呈现多元化倾向.那么,复数有哪些表现形式呢?除了坐标表示,还有什么表示方法呢?激趣诱思知识点拨一、复数的三角表示式 激趣诱思知识点拨于是,任何复数z=a+bi(a,b∈R)都可以表示为z=r(cos θ+isin θ),其中这个式子称为复数z=a+bi(a,b∈R)的三角表示式,简称三角形式.为了与三角形式区分,a+bi称为复数的代数表示式,简称代数形式.当z=r(cos θ+isin θ)≠0时,z的辐角有无穷多个值,这些值相差2π的整数倍.为确定起见,将满足条件0≤θ<2π的辐角值,称为辐角的主值,记作arg z,即0≤arg z<2π.每一个非零复数有唯一的模与辐角的主值,并且可由它的模与辐角的主值唯一确定.因此,两个非零复数相等,当且仅当它们的模与辐角的主值分别相等.显然当a>0时,arg a=0,arg(-a)=π,arg(ai)如果z=0,那么与它对应的向量 缩成一个点(零向量),它的方向是任意的,所以复数0的辐角也是任意的.激趣诱思知识点拨名师点析(1)复数的三角形式的特征:①模r≥0.②括号内需满足:前余弦,后正弦,角相同.③cos θ与isin θ之间用加号连结.简单地说,复数三角形式的结构特征是:模非负,角相同,余弦前,加号连.不符合条件的都不是三角形式.(2)在复数的三角形式中,幅角θ的值可以用弧度表示,也可以用角度表示,可以是主值,也可以是主值加2kπ或k·360°(k∈Z).但为了简单起见,复数的代数形式化为三角形式时,一般将θ写成主值.激趣诱思知识点拨微思考(1)复数a+bi(a,b∈R)与复平面内的点和向量是如何一一对应的?提示根据复平面的建立原则,复数a+bi与复平面内的点Z(a,b)是一一对应的,与平面向量 =(a,b)也是一一对应的.(2)若角θ的顶点在坐标原点,始边在x轴非负半轴上,已知终边上一点P(x,y),如何表示角θ的三角函数?(3)终边相同的角有什么关系?提示终边相同的角相差2π的整数倍.激趣诱思知识点拨微练习1写出下列复数的辐角主值:激趣诱思知识点拨答案A 激趣诱思知识点拨二、复数三角形式的乘法法则与几何意义1.复数乘法运算的三角表示若z1=r1(cos θ1+isin θ1),z2=r2(cos θ2+isin θ2),则z1z2=r1r2·[cos(θ1+θ2)+isin(θ1+θ2)].两个复数相乘,积的模等于它们模的积,积的辐角等于它们辐角的和.简单地说,两个复数三角形式相乘的法则为:模数相乘,幅角相加.2.复数乘法运算的几何意义激趣诱思知识点拨微拓展使用复数的三角形式进行运算的条件是复数必须是三角形式的标准式,辐角不要求一定是主值.激趣诱思知识点拨微练习计算下列各式,并把结果化为代数形式.激趣诱思知识点拨激趣诱思知识点拨三、复数三角形式的除法法则与几何意义1.复数除法运算的三角表示若z1=r1(cos θ1+isin θ1),z2=r2(cos θ2+isin θ2),则z1÷z2= [cos(θ1-θ2)+isin(θ1-θ2)].两个复数相除,商的模等于被除数的模除以除数的模,商的辐角等于被除数的辐角减去除数的辐角所得的差.简单地说,两个复数三角形式相除的法则为:模数相除,幅角相减.2.复数除法运算的几何意义激趣诱思知识点拨名师点析两个复数相除等于它们的模相除而幅角相减,这个运算在几何上可以用下面的方法进行:将向量z1的模缩小为原来的 ,然后再将它绕原点顺时针旋转角θ2,就得到z1,z2的商.激趣诱思知识点拨微练习1计算下列各式:激趣诱思知识点拨微练习2 探究一探究二探究三探究四当堂检测复数的三角形式例1将下列复数表示成三角形式(辐角取主值).探究一探究二探究三探究四当堂检测探究一探究二探究三探究四当堂检测反思感悟 复数的代数形式z=a+bi化为复数三角形式的一般步骤是:③写出复数的三角形式.探究一探究二探究三探究四当堂检测变式训练1将下列复数中代数形式的表示成三角形式(辐角取主值),三角形式的表示成代数形式.探究一探究二探究三探究四当堂检测探究一探究二探究三探究四当堂检测复数三角形式的乘法运算例2计算下列各式探究一探究二探究三探究四当堂检测探究一探究二探究三探究四当堂检测反思感悟 两个复数三角形式乘法的法则可简记为,模数相乘,辐角相加,并且可以作以下推广:(1)有限个复数相乘,结论亦成立.即z1·z2…zn=r1(cos θ1+isin θ1)·r2(cos θ2+isin θ2)…rn(cos θn+isin θn)=r1·r2…rn[cos(θ1+θ2+…+θn)+isin(θ1+θ2+…+θn)].(2)当z1=z2=…=zn=z时,即r1=r2=…=rn=r,θ1=θ2=…=θn=θ,有zn=[r(cos θ+isin θ)]n=rn(cos nθ+isin nθ),这就是复数三角形式的乘方法则,即:模数乘方,辐角n倍.探究一探究二探究三探究四当堂检测探究一探究二探究三探究四当堂检测探究一探究二探究三探究四当堂检测复数三角形式的除法运算例3计算下列各式探究一探究二探究三探究四当堂检测反思感悟 进行两个复数的三角形式除法运算时,将模对应相除当模,用被除数辐角减去除数的辐角当做商的辐角,即可得两个复数的除法结果.探究一探究二探究三探究四当堂检测变式训练3计算下列各式 探究一探究二探究三探究四当堂检测复数乘除法运算的几何意义例4已知复数乘法(x+yi)(cos θ+isin θ)(x,y∈R,i为虚数单位)的几何意义是将复数x+yi在复平面内对应的点(x,y)绕原点逆时针方向旋转θ角,则将点(6,4)绕原点逆时针方向旋转 得到的点的坐标为　　　　　. 探究一探究二探究三探究四当堂检测反思感悟 逆时针方向旋转与复数的乘法的几何意义相对应;顺时针方向旋转与复数的除法的几何意义相对应.可简记为“逆乘顺除”四个字.探究一探究二探究三探究四当堂检测延伸探究若将条件“逆时针方向”改为“顺时针方向”,其结果如何? 探究一探究二探究三探究四当堂检测答案B 探究一探究二探究三探究四当堂检测答案A 探究一探究二探究三探究四当堂检测