


















































































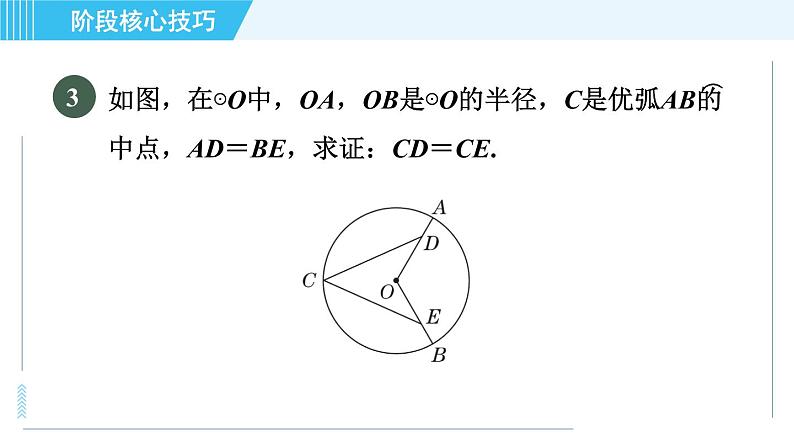







数学九年级上册第2章 对称图形——圆综合与测试习题课件ppt
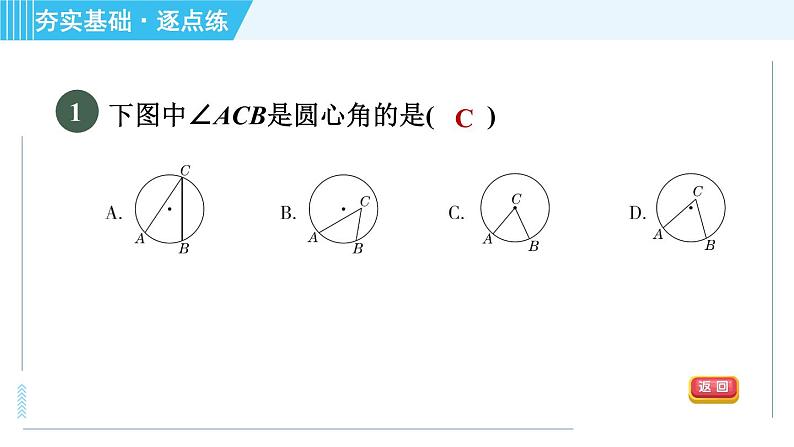
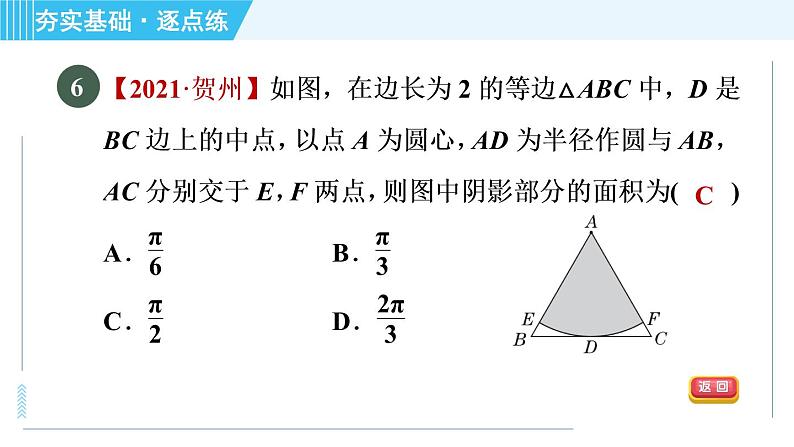
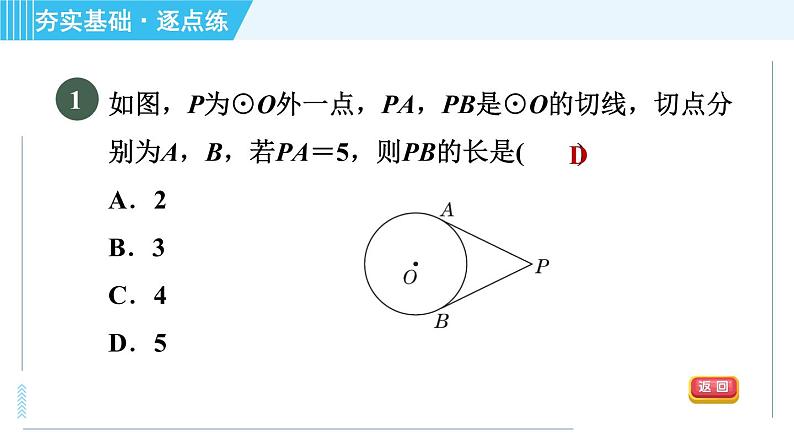
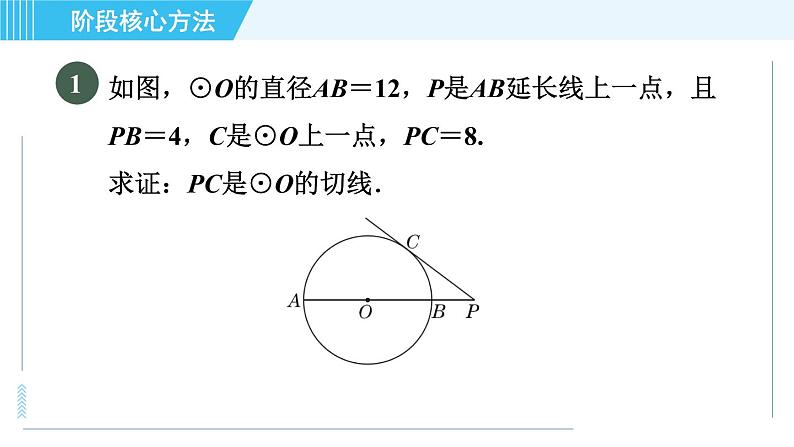
展开如图,P为⊙O外一点,PA,PB是⊙O的切线,切点分别为A,B,若PA=5,则PB的长是( )A.2 B.3 C.4 D.5
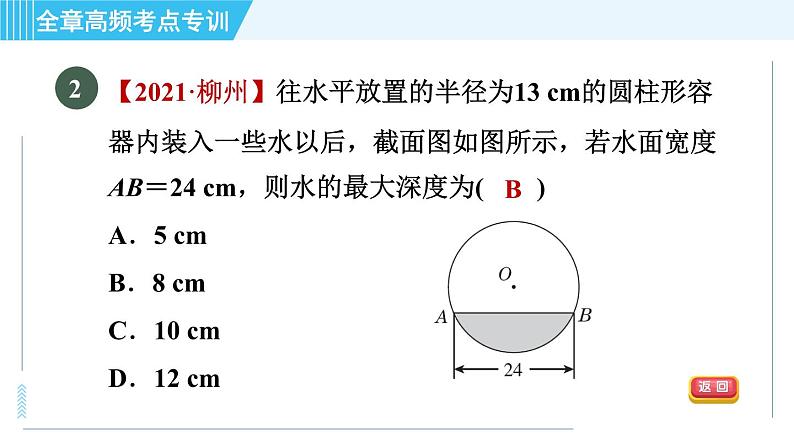
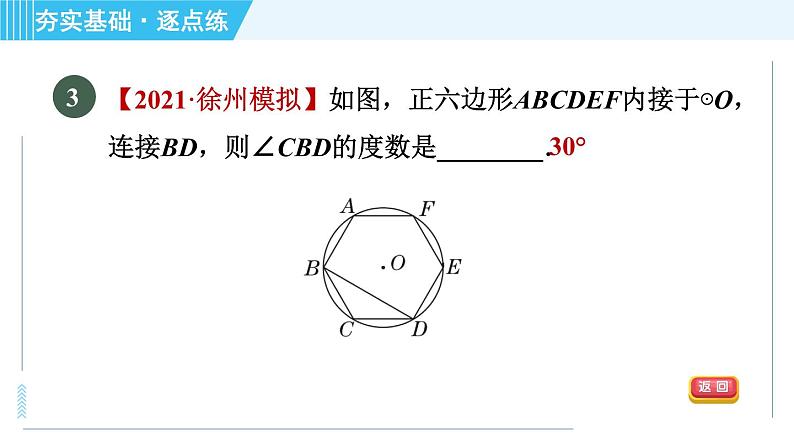
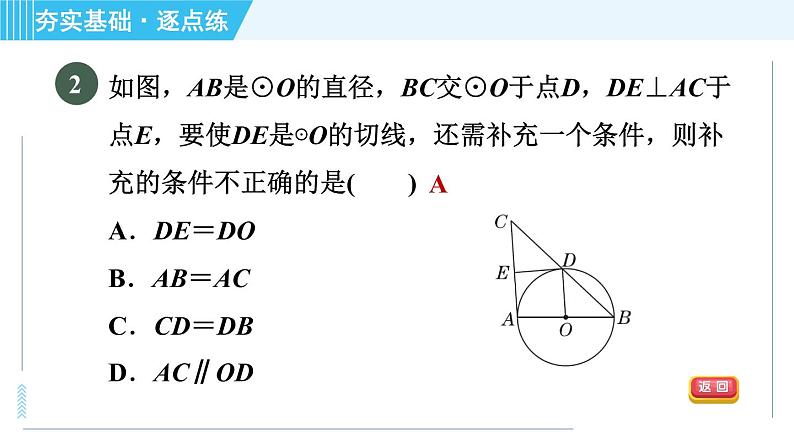
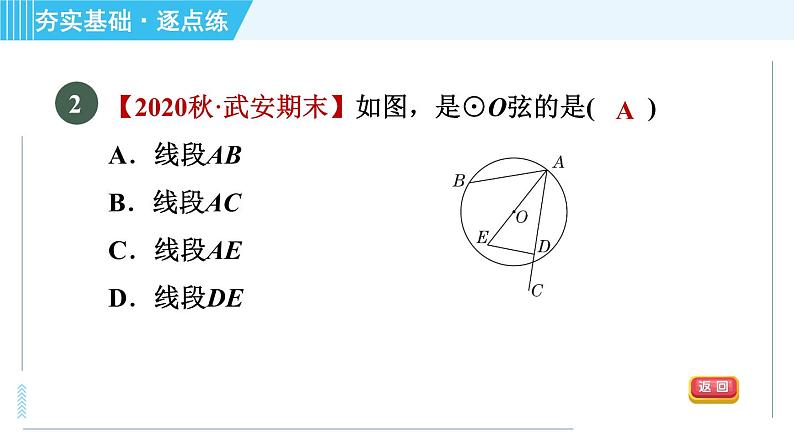
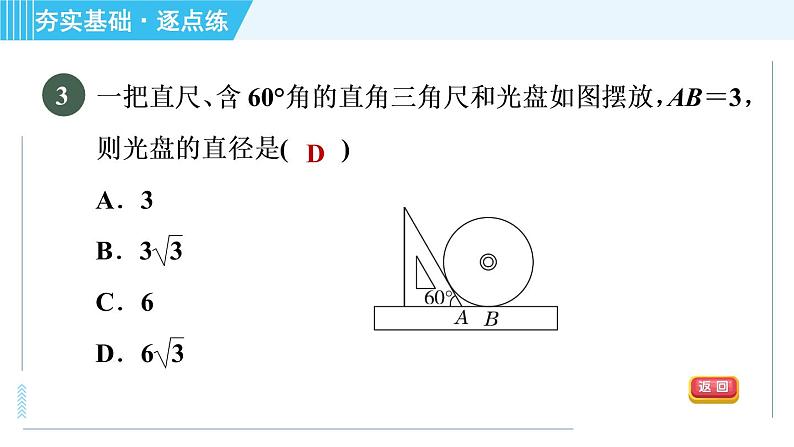
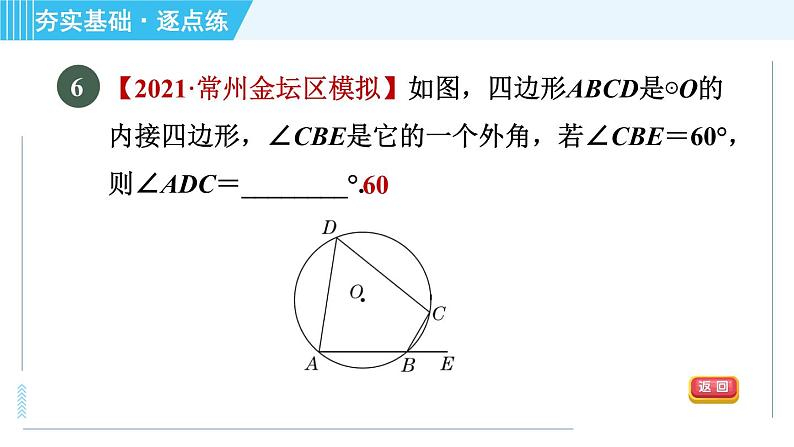
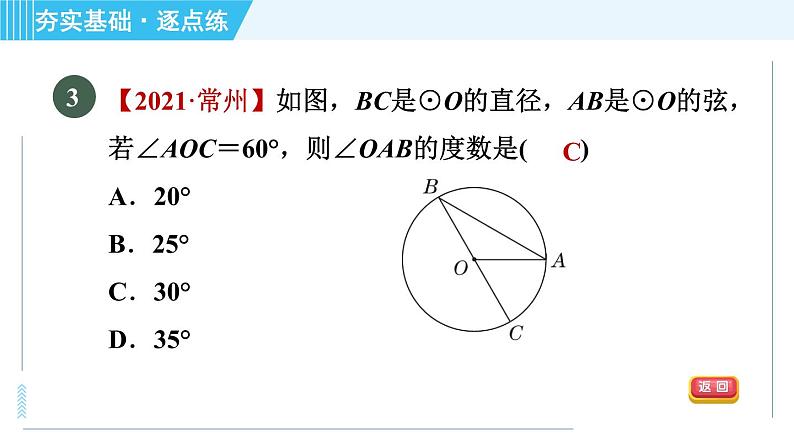
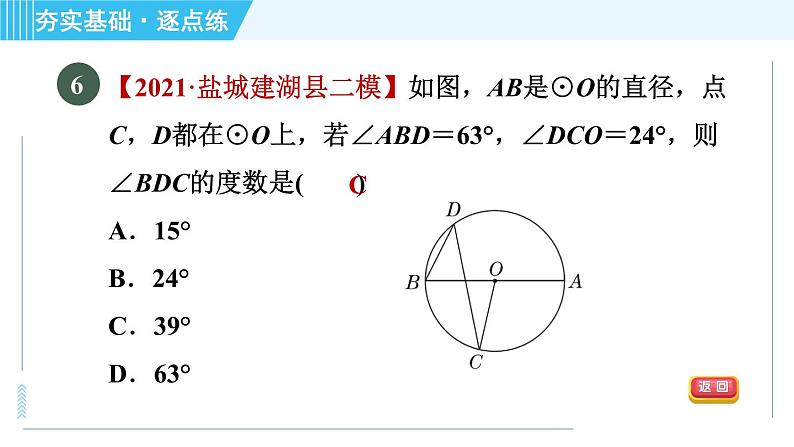
【中考·益阳】如图,PA,PB是⊙O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交⊙O于点D,下列结论不一定成立的是( )A.PA=PB B.∠BPD=∠APDC.AB⊥PD D.AB平分PD
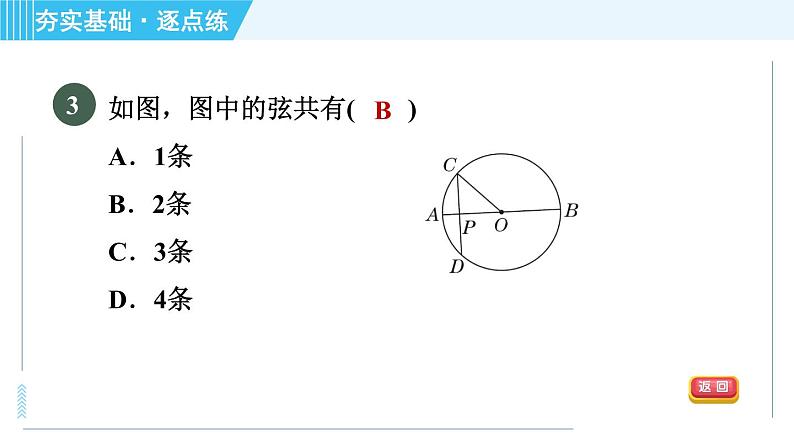
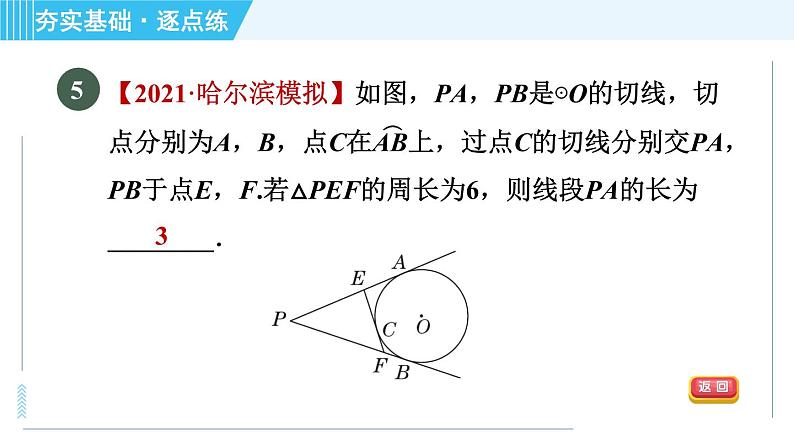
【2021·哈尔滨模拟】如图,PA,PB是⊙O的切线,切点分别为A,B,点C在AB上,过点C的切线分别交PA,PB于点E,F.若△PEF的周长为6,则线段PA的长为________.
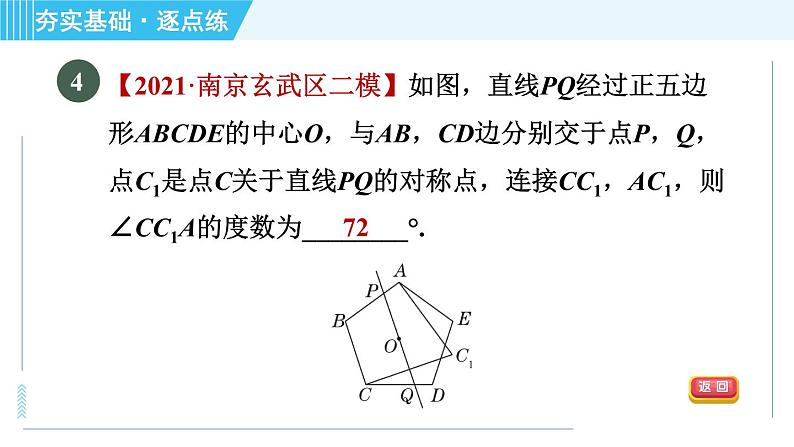
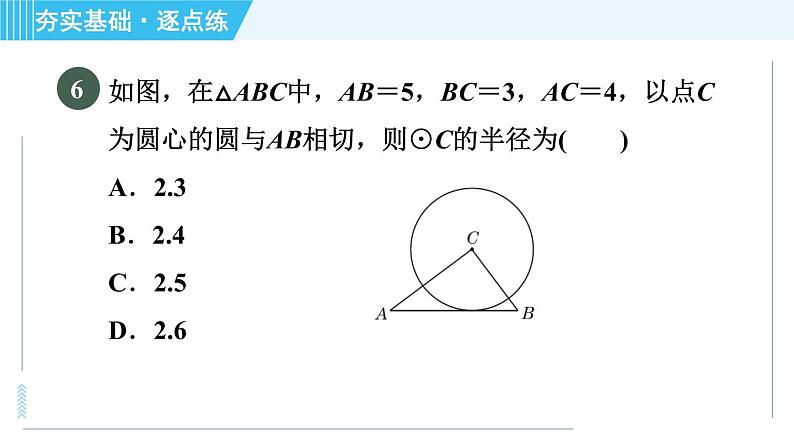
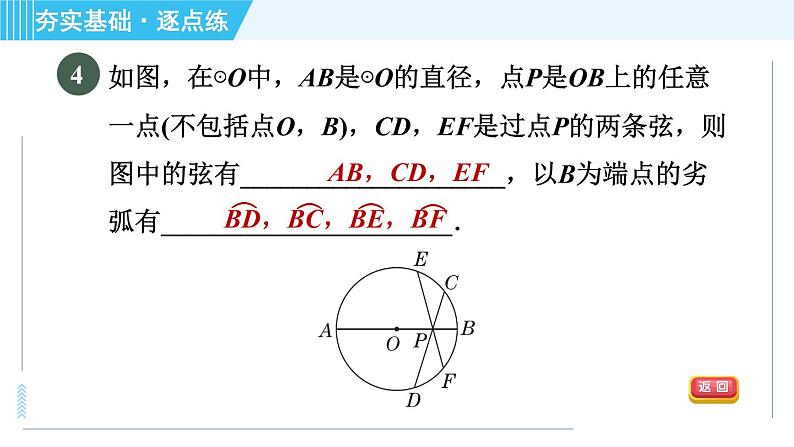
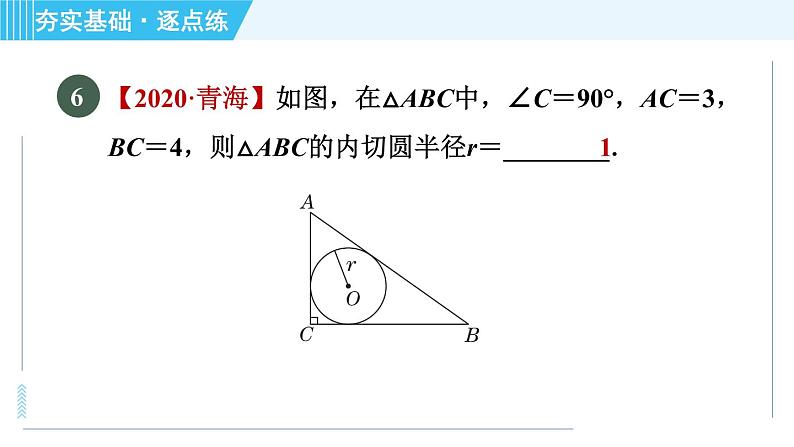
【2020·青海】如图,在△ABC中,∠C=90°,AC=3,BC=4,则△ABC的内切圆半径r=________.
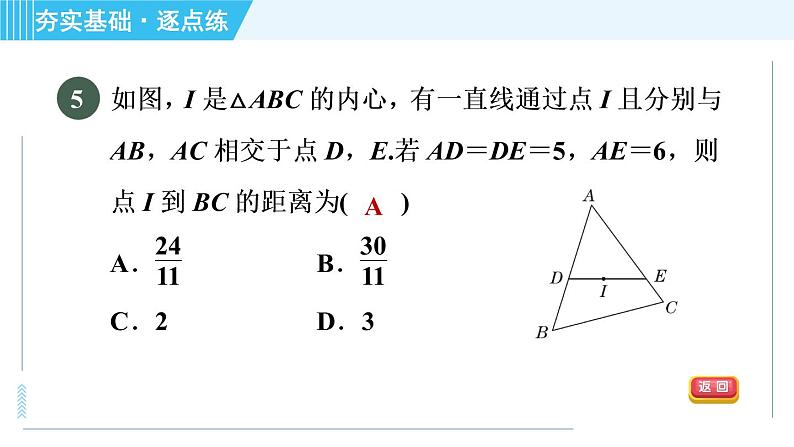
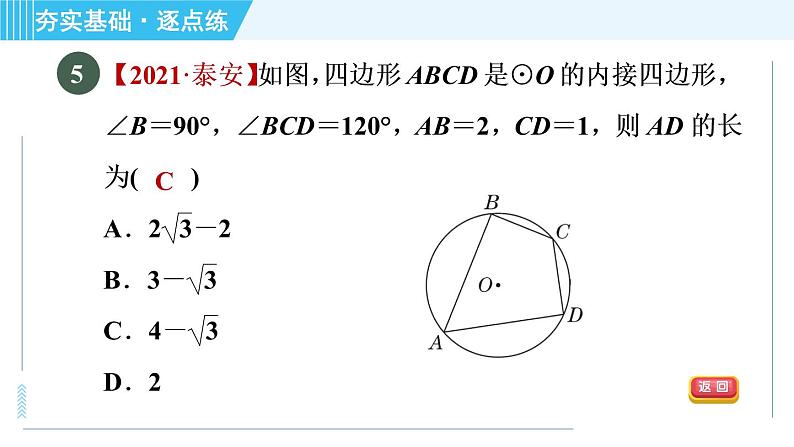
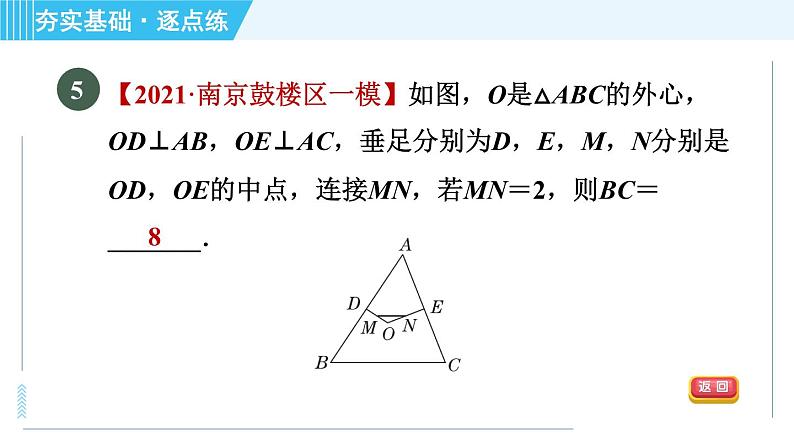
【点拨】在△ABC中,∠C=90°,AC=3,BC=4,根据勾股定理,得AB=5,如图,设△ABC的内切圆与三条边的切点分别为D,E,F,连接OD,OE,OF.∴OD⊥AB,OE⊥BC,OF⊥AC,可得矩形EOFC,根据切线长定理,得CE=CF,∴矩形EOFC是正方形.
设CE=CF=r,则AF=AD=AC-FC=3-r,BE=BD=BC-CE=4-r,∵AD+BD=AB,∴3-r+4-r=5,解得r=1.∴△ABC的内切圆半径r=1.
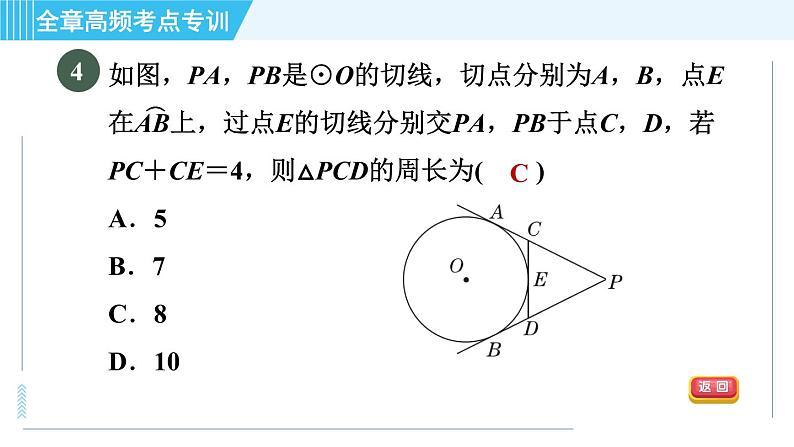
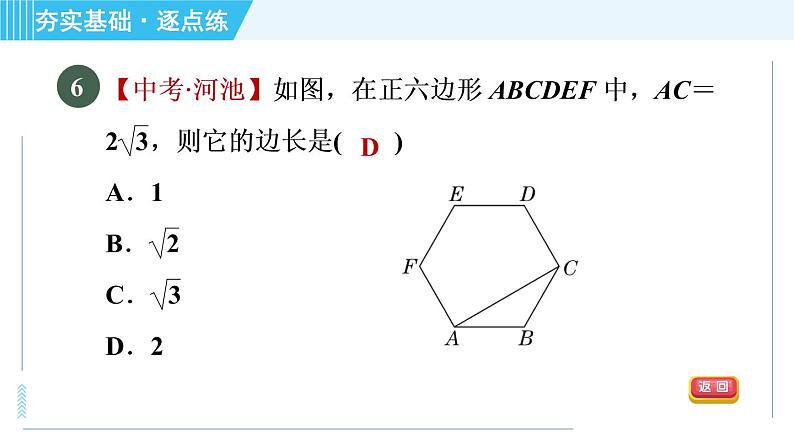
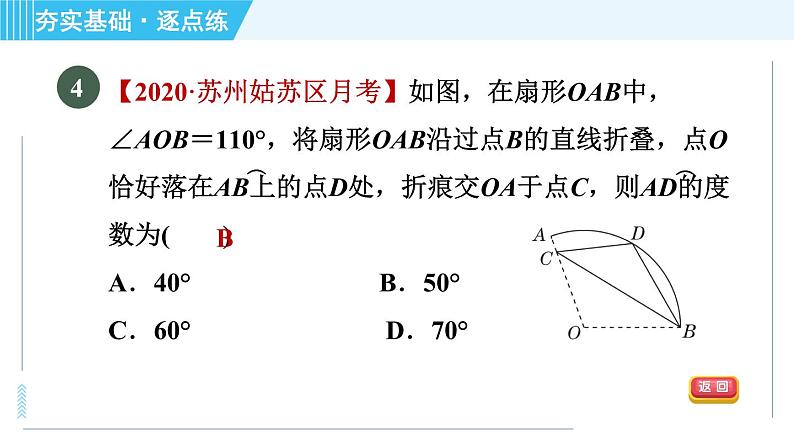
【2021·盐城滨海县一模】如图,PA,PB是⊙O的切线,切点分别为A,B,点E在AB上,过点E的切线分别交PA,PB于点C,D.△PCD的周长为12,∠APB=60°.求:
解:∵CA、CE都是⊙O的切线,∴CA=CE(过圆外一点所画的圆的两条切线长相等).同理DE=DB,PA=PB,∴△PCD的周长=PD+CD+PC=PD+CE+DE+PC=PD+CA+DB+PC=PA+PB=2PA=12,即PA的长为6.
(2)求∠COD的度数.
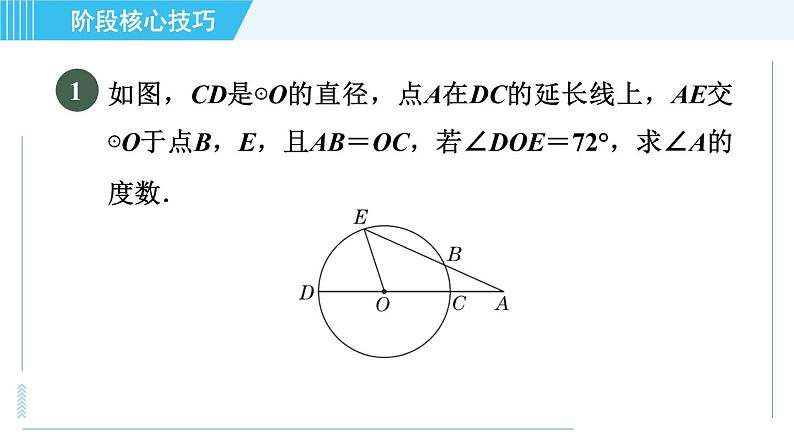
(1)如图①,四边形ABCD的各边与⊙O分别相切于点E,F,G,H,说明AB+CD与BC+AD的大小关系;
解:由切线长定理,得AE=AH,BE=BF,CF=CG,DG=DH,∴AB+CD=AE+BE+CG+DG=AH+BF+CF+DH=AH+DH+BF+CF=BC+AD,即AB+CD=BC+AD.
(2)如图②,四边形ABCD的三边与⊙O分别相切于点F,G,H,说明AB+CD与BC+AD的大小关系.
解:过点B作⊙O的切线,交AD于点M.由(1)可知BM+CD=BC+MD.∵AB<AM+BM,∴AB+BM+CD<AM+BM+BC+MD,∴AB+CD<BC+AD.
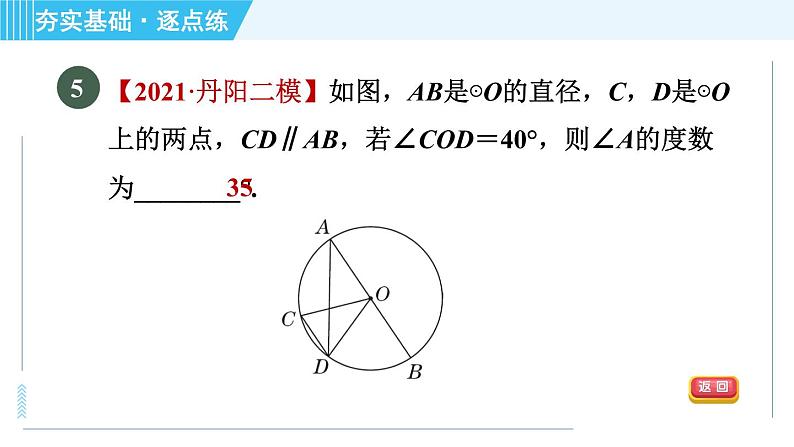
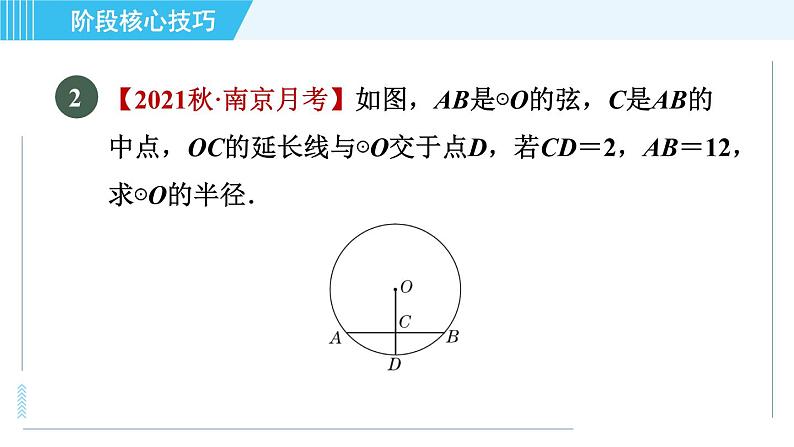
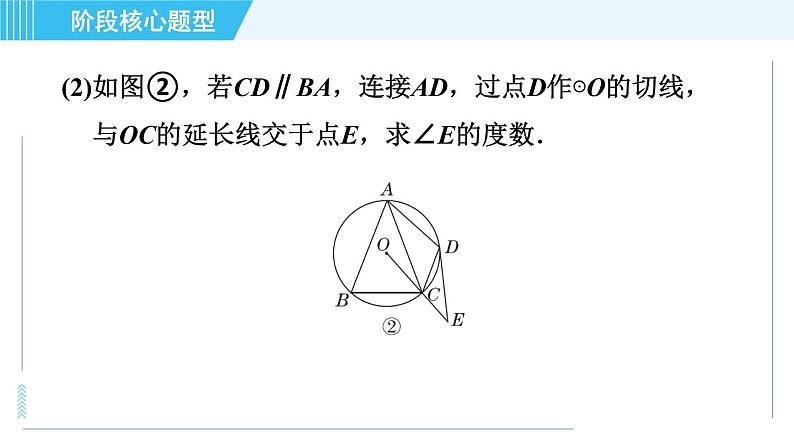
已知:AB是⊙O的直径,AB=2,弦DE=1,直线AD与BE相交于点C,弦DE在⊙O上运动且保持长度不变,过点D的切线交BC于点F.(1)如图①,若DE∥AB,求证:CF=EF;
证明:如图,连接OD,OE.∵AB=2,∴OA=OD=OE=OB=1.∵DE=1,∴OD=OE=DE.∴△ODE是等边三角形.∴∠ODE=∠OED=60°.∵DE∥AB,∴∠AOD=∠ODE=60°,∠BOE=∠OED=60°.∴△AOD和△BOE都是等边三角形.∴∠OAD=∠OBE=60°.
∵DE∥AB,∴∠CDE=∠OAD=60°,∠CED=∠OBE=60°.∴△CDE是等边三角形.∵DF是⊙O的切线,∴DF⊥OD.∴∠ODF=90°.∴∠EDF=90°-∠CED=90°-60°=30°.∴∠DFE=180°-∠EDF-∠CED=180°-30°-60°=90°.∴DF⊥CE.∴CF=EF.
(2)如图②,当点E运动至与点B重合时,试判断CF与BF是否相等,并说明理由.
数学九年级上册第1章 一元二次方程综合与测试习题ppt课件: 这是一份数学九年级上册第1章 一元二次方程综合与测试习题ppt课件
初中数学苏科版九年级上册2.5 直线与圆的位置关系习题ppt课件: 这是一份初中数学苏科版九年级上册2.5 直线与圆的位置关系习题ppt课件,共20页。PPT课件主要包含了答案呈现,习题链接,1求PA的长等内容,欢迎下载使用。
初中数学苏科版九年级上册1.2 一元二次方程的解法习题ppt课件: 这是一份初中数学苏科版九年级上册1.2 一元二次方程的解法习题ppt课件,共20页。PPT课件主要包含了答案呈现,习题链接,x=3a或x=-a等内容,欢迎下载使用。