数学4 二次函数的应用测试题

这是一份数学4 二次函数的应用测试题，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
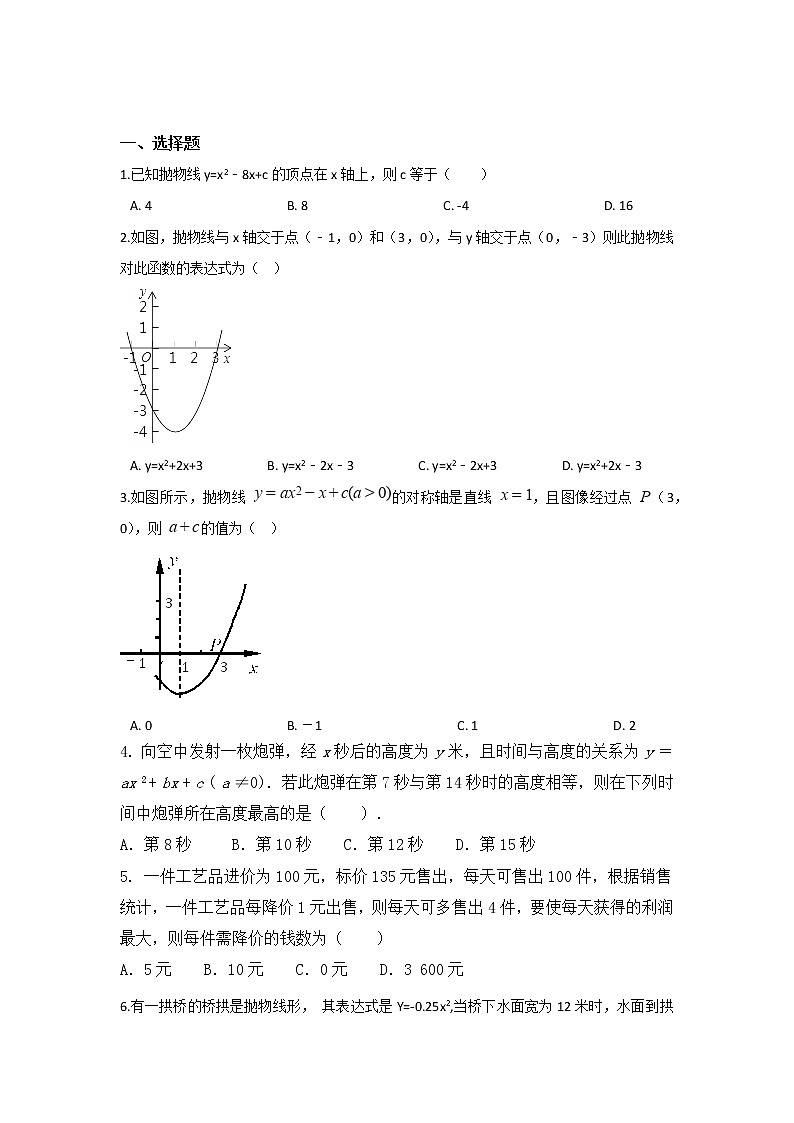
 一、选择题 1.已知抛物线y=x2﹣8x+c的顶点在x轴上，则c等于（　　）            A. 4                                          B. 8                                          C. -4                                          D. 162.如图，抛物线与x轴交于点（﹣1，0）和（3，0），与y轴交于点（0，﹣3）则此抛物线对此函数的表达式为（   ）
 A. y=x2+2x+3                   B. y=x2﹣2x﹣3                   C. y=x2﹣2x+3                   D. y=x2+2x﹣33.如图所示，抛物线 的对称轴是直线 ，且图像经过点 （3，0），则 的值为（   ）
 A. 0                                          B. －1                                          C. 1                                          D. 24. 向空中发射一枚炮弹，经 x 秒后的高度为 y 米，且时间与高度的关系为 y ＝ ax 2 + bx + c ( a ≠0)．若此炮弹在第7秒与第14秒时的高度相等，则在下列时间中炮弹所在高度最高的是（　　）． A．第8秒   B．第10秒   C．第12秒   D．第15秒 5. 一件工艺品进价为100元，标价135元售出，每天可售出100件，根据销售统计，一件工艺品每降价1元出售，则每天可多售出4件，要使每天获得的利润最大，则每件需降价的钱数为（　　） A．5元   B．10元   C．0元   D．3 600元 6.有一拱桥的桥拱是抛物线形， 其表达式是Y=-0.25x2,当桥下水面宽为12米时，水面到拱桥拱顶的距离为（      ）             A. 3米                                 B. 2 米                                 C. 4 米                                 D. 9米7. 某厂有许多形状为直角梯形的铁皮边角料，为节约资源，现要按图中所示的方法从这些边角料上截取矩形(阴影部分)铁皮备用，当截取的矩形面积最大时，矩形两边长 x ， y 应分别为（　　） A． x ＝10， y ＝14   B． x ＝14， y ＝10 C． x ＝12， y ＝15   D． x ＝15， y ＝12 8.如图为一座抛物线型的拱桥，AB、CD分别表示两个不同位置的水面宽度，O为拱桥顶部，水面AB宽为10米，AB距桥顶O的高度为12.5米，水面上升2.5米到达警戒水位CD位置时，水面宽为（　　）米．
 A. 5                                        B. 2                                        C. 4                                        D. 89.某种电缆在空中架设时，两端挂起的电缆下垂都近似抛物线y=x2的形状．今在一个坡度为1：5的斜坡上，沿水平距离间隔50米架设两固定电缆的位置离地面高度为20米的塔柱（如图），这种情况下在竖直方向上，下垂的电缆与地面的最近距离为（　　）
 A. 12.75米                             B. 13.75米                             C. 14.75米                             D. 17.75米二、填空题 10.已知抛物线y=ax2+bx+c经过A（﹣3，0），B（1，0），C（0，3），则该抛物线的解析式为________ ．    11.请写出一个开口向下，并且与x轴只有一个公共点的抛物线的解析式，y=________ ．    12.若抛物线y=ax2+c与y=2x2的形状相同，开口方向相反，且其顶点坐标是（0，﹣2），则该抛物线的函数表达式是________ ． 13.用长度一定的绳子围成一个矩形，如果矩形的一边长x(m)与面积y(m2)满足函数关系y＝－(x－12)2＋144(0＜x＜24)，那么该矩形面积的最大值为________m2 ．   14. 某种商品每件进价为20元，调查表明：在某段时间内若以每件x元（20≤x≤30，且x为整数）出售，可卖出（30﹣x）件．若使利润最大，每件的售价应为 ________元．   15. 将一条长为20cm的铁丝剪成两段，并以每一段铁丝的长度为周长各做成一个正方形，则这两个正方形面积之和的最小值是  cm2．16. 某种火箭竖直向上发射时，它的高度 h (m)与时间 t (s)的关系可以用 h ＝－5 t 2 +150 t +10表示．经过__________ s，火箭达到它的最高点．17.如图是某拱形大桥的示意图，桥拱与桥面的交点为O，B，以点O为原点，水平直线OB为x轴，建立平面直角坐标系，桥的拱形可以近似看成抛物线y=﹣ （x﹣80）2+16，桥拱与桥墩AC的交点C恰好在水面，有AC⊥x轴．若OA=10米，则桥面离水面的高度AC为________米．
 三、解答题 18.已知二次函数当x=﹣1时，有最小值﹣4，且当x=0时，y=﹣3，求二次函数的解析式．            19.用长为32米的篱笆围一个矩形养鸡场，设围成的矩形一边长为x米，面积为y平方米．
（1）求y关于x的函数关系式；
（2）当x为何值时，围成的养鸡场面积为60平方米？
（3）能否围成面积为70平方米的养鸡场？如果能，请求出其边长；如果不能，请说明理由．         20.拱桥的形状是抛物线，其函数关系式为 ，当水面离桥顶的高度为 m时，水面的宽度为多少米？
       21.某公司经营一种绿茶，每千克成本为50元．市场调查发现，在一段时间内，销售量w（千克）随销售单价x（元/千克）的变化而变化，具体关系式为：w＝－2x＋240.设这种绿茶在这段时间的销售利润为y（元），解答下列问题：
（1）求y与x的关系式
（2）当x取何值时，销售利润最大？最大利润是多少？            22.在平面直角坐标系中，已知抛物线经过A（﹣4，0），B（0，﹣4），C（2，0）三点．  （1）求抛物线的解析式；    （2）若点M为第三象限内抛物线上一动点，点M的横坐标为m，△AMB的面积为S．  求S关于m的函数关系式，并求出S的最大值．    （3）若点P是抛物线上的动点，点Q是直线y=﹣x上的动点，判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形，直接写出相应的点Q的坐标．