2020-2021学年第18章 平行四边形18.2 平行四边形的判定第3课时导学案

这是一份2020-2021学年第18章 平行四边形18.2 平行四边形的判定第3课时导学案，共2页。学案主要包含了学习目标，自学互助，合作探究、质疑拓展，检测互评，归纳总结等内容，欢迎下载使用。
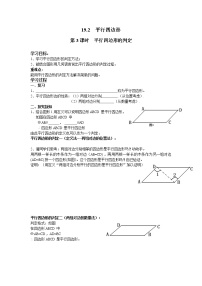
18.2.3 平行四边形的性质和判定的应用【学习目标】1.学会综合应用几种判定方法。2.熟练选择几种判定方法。【自学互助】1.平行四边的性质:2.平行四边形的判定方法:【合作探究、质疑拓展】1．已知：如图，在□ABCD中，点E、F在对角线AC上，且AE＝CF．请你以F为一个端点，和图中已标明字母的某一点连成一条新线段，猜想并证明它和图中已有的某一条线段相等(只需证明一组线段相等即可)．(1)连结______；(2)猜想：______＝______；(3)证明：    2．如图，在△ABC中，EF为△ABC的中位线，D为BC边上一点(不与B、C重合)，AD与EF交于点O，连结DE、DF，要使四边形AEDF为平行四边形，需要添加条件____      ．(只添加一个条件)证明：     3．如图，在□ABCD中，E、F分别是边AD、BC上的点，已知AE＝CF，AF与BE相交于点G，CE与DF相交于点H，求证：四边形EGFH是平行四边形．      【检测互评】1．如图，在□ABCD中，E、F分别在边BA、DC的延长线上，已知AE＝CF，P、Q分别是DE和FB的中点，求证：四边形EQFP是平行四边形．     2．如图，在□ABCD中，E、F分别在DA、BC的延长线上，已知AE＝CF，FA与BE的延长线相交于点R，EC与DF的延长线相交于点S，求证：四边形RESF是平行四边形．3．已知：如图，四边形ABCD中，AB＝DC，AD＝BC，点E在BC上，点F在AD上，AF＝CE，EF与对角线BD交于点O，求证：O是BD的中点． 4．已知：如图，△ABC中，D是AC的中点，E是线段BC延长线上一点，过点A作BE的平行线与线段ED的延长线交于点F，连结AE、CF．求证：CF∥AE.     【归纳总结】