

青海省海东市2021届高三第二次模拟考试数学(文)试题含答案
展开高三数学试卷(文科)
第Ⅰ卷
一、选择题:在每小题给出的四个选项中,只有一项是符合题自要求的.
1. 设集合,,则( ).
A. B. C. D.
【答案】D
2. ( )
A. B. C. 10 D.
【答案】D
3. 设向量,,若,则( ).
A. B. C. D.
【答案】B
4. 双曲线的渐近线方程为,则( )
A. 4 B. 2 C. D.
【答案】A
5. 如图,根据已知的散点图,得到y关于x的线性回归方程为,则( )
A. 1.5 B. 1.8 C. 2 D. 1.6
【答案】D
6. 设,是两个不同的平面,,,是三条不同的直线.下列说法不正确的是( )
A. 若,,则 B. 若,,则
C. 若,,则 D. 若,,,,则
【答案】C
7. 抛物线上一点到焦点F的距离为( )
A. B. 5 C. D. 33
【答案】C
8. 已知都是正实数,则“”是“”的( )
A. 充要条件 B. 必要不充分条件
C. 充分不必要条件 D. 既不充分也不必要条件
【答案】A
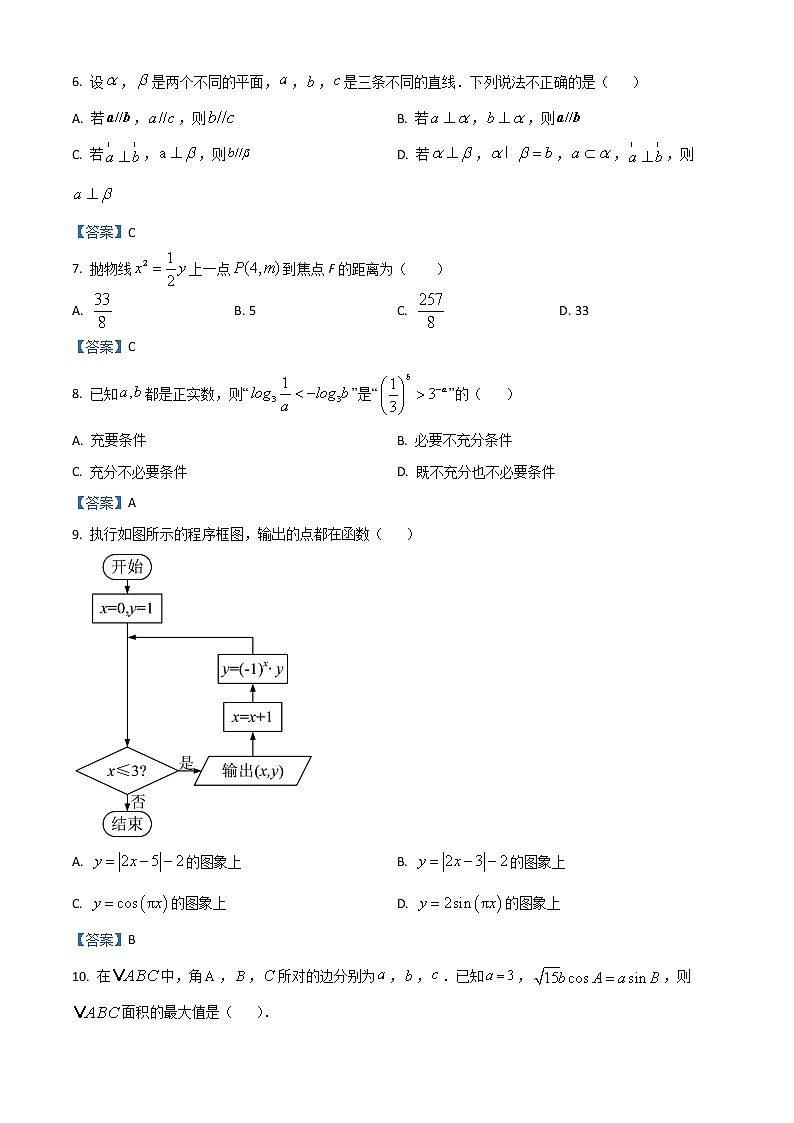
9. 执行如图所示的程序框图,输出的点都在函数( )
A. 的图象上 B. 的图象上
C. 的图象上 D. 的图象上
【答案】B
10. 在中,角,,所对的边分别为,,.已知,,则面积的最大值是( ).
A. B. C. D.
【答案】B
11. 早期的毕达哥拉斯学派学者注意到用等边三角形或正方形为表面可构成四种规则的立体图形,即正四面体、正六面体、正八面体和正二十面体,它们的各个面和多面角都全等.已知正二十面体是由20个等边三角形所组成的正多面体,共有12个顶点,30条棱,20个面,正二十面体的体积公式为(其中为棱长),已知一个正二十面体各棱长之和为,则该正二十面体内切球的半径为( )
A. B. C. D.
【答案】B
12. 已知函数.若,则大小关系是( )
A. B. C. D.
【答案】C
第Ⅱ卷
二、填空题:
13. ___________.
【答案】
14. 若x,y满足约束条件,则的最大值为________.
【答案】15
15. 黄金矩形的短边与长边的比值为黄金分割比.黄金矩形能够给画面带来美感,如图,在黄金矩形画框中设,则________.
【答案】
16. 如图,已知抛物线,圆,过圆心的直线与抛物线和圆依次交于,,,,则______.
【答案】4
三、解答题:解答应写出必要的文字说明、证明过程或演算步骤.17~21题为必考题,每个试题考生都必须作答.第22,23题为选考题,考生根据要求作答.
(一)必考题
17. 已知是等差数列,,.
(1)求的通项公式;
(2)求数列的前n项和.
【答案】(1);(2).
18. 为了解中学生是否近视与性别的相关性,某研究机构分别调查了甲、乙、丙三个地区的100名中学生是否近视的情况,得到三个列联表如表所示.
甲地区 乙地区 丙地区
| 近视 | 不近视 | 合计 |
|
| 近视 | 不近视 | 合计 |
|
| 近视 | 不近视 | 合计 |
男 | 21 | 29 | 50 | 男 | 25 | 25 | 50 | 男 | 23 | 27 | 50 | ||
女 | 19 | 31 | 50 | 女 | 15 | 35 | 50 | 女 | 17 | 33 | 50 | ||
合计 | 40 | 60 | 100 | 合计 | 40 | 60 | 100 | 合计 | 40 | 60 | 100 |
(1)分别估计甲、乙两地区的中学男生中男生近视的概率;
(2)根据列联表的数据,在这三个地区中,中学生是否近视与性别关联性最强与最弱的地区分别是哪个地区?
附:,其中.
【答案】(1)0.42;0.5;(2)在这三个地区中,乙地区的中学生是否近视与性别关联性最强,甲地区的中学生是否近视与性别关联性最弱.
19. 如图,在三棱锥中,
(1)证明:平面平面.
(2)在侧面内求作一点H,使得平面,写出作法(无需证明),并求线段的长.
【答案】(1)证明见解析;(2)答案见解析,.
20. 已知椭圆的离心率为,且焦距为8.
(1)求C的方程;
(2)设直线l的倾斜角为,且与C交于A,B两点,求(O为坐标原点)面积的最大值.
【答案】(1);(2).
21. 已知函数.
(1)当时,求曲线在点处的切线方程;
(2)若关于方程在上有解,求实数的取值范围.
【答案】(1);(2)
(二)选考题:
[选修4-4:坐标系与参数方程]
22. 太极图被称为“中华第一图”.从孔庙大成殿梁柱,到楼观台、三茅宫标记物;从道袍、卦摊、中医、气功、武术到韩国国旗……,太极图无不跃居其上.这种广为人知的太极图,其形状如阴阳两鱼互抱在一起,因而被称为“阴阳鱼太极图”.在如图所示的极坐标中,阴阳鱼图案中实线部分中的弧,,所在圆的圆心分别为,,,曲线是弧,曲线是弧,曲线是弧.
(1)分别写出,,极坐标方程;
(2)曲线由,,构成,若点在上,且,求的极坐标.
【答案】(1),,;(2)的极坐标为,.
[选修4-5:不等式选讲]
23. 已知函数.
(1)当时,求不等式解集;
(2)若时,,求的取值范围.
【答案】(1);(2).
2020青海省海东市高三第五次模拟考试数学(理)试题扫描版含答案: 这是一份2020青海省海东市高三第五次模拟考试数学(理)试题扫描版含答案
2020青海省海东市高三第五次模拟考试数学(文)试题扫描版含答案: 这是一份2020青海省海东市高三第五次模拟考试数学(文)试题扫描版含答案
2021青海省海东市高三第一次模拟考试数学(文)试题扫描版含答案: 这是一份2021青海省海东市高三第一次模拟考试数学(文)试题扫描版含答案












