高中数学北师大版 (2019)必修 第一册1.2 集合的基本关系学案设计

这是一份高中数学北师大版 (2019)必修 第一册1.2 集合的基本关系学案设计，共8页。


草原上，蓝蓝的天上白云飘，白云下面马儿跑．如果草原上的枣红马组成集合A，草原上的所有马组成集合B.
[问题] (1)集合A中的元素与集合B中的元素的关系是怎样的？
(2)集合A与集合B又存在什么关系？





知识点 子集、集合相等、真子集
1．Venn图
用平面上封闭曲线的内部表示集合，称为Venn图．
2．子集、集合相等、真子集
eq \a\vs4\al()
1．用Venn图表示集合的优点是能直观地表示集合间的关系，缺点是集合元素的公共特征不明显．
2．真子集概念的理解
在真子集的定义中，A，B首先要满足A⊆B，其次至少有一个x∈B，但x∉A.
1．任意两个集合之间是否有包含关系？
提示：不一定，如集合A＝{1，3}，B＝{2，3}，这两个集合就没有包含关系．
2．符号“∈”与“⊆”有什么区别？
提示：①“∈”是表示元素与集合之间的关系，比如1∈N，－1∉N.
②“⊆”是表示集合与集合之间的关系，比如N⊆R，{1，2，3}⊆{3，2，1}．
③“∈”的左边是元素，右边是集合，而“⊆”的两边均为集合．
1．下列Venn图正确表示集合M＝{－1，0，1}和N＝{x|x2－x＝0}的关系的是( )
解析：选B 由N＝{1，0}，知NM，故选B.
2．设a∈R，若集合{2，9}＝{1－a，9}，则a＝________．
解析：因为{2，9}＝{1－a，9}，则2＝1－a，所以a＝－1.
答案：－1
[例1] (链接教科书第7页练习2题)集合M＝{x|x＝5k－2，k∈Z}，P＝{x|x＝5n＋3，n∈Z}，S＝{x|x＝10m＋3，m∈Z}之间的关系是( )
A．SPM B．S＝PM
C．SP＝M D．P＝MS
[解析] ∵M＝{x|x＝5k－2，k∈Z}，P＝{x|x＝5n＋3，n∈Z}，S＝{x|x＝10m＋3，m∈Z}，∴M＝{…，－7，－2，3，8，13，18，…}，P＝{…，－7，－2，3，8，13，18，…}，S＝{…，－7，3，13，23，…}，故SP＝M，故选C.
[答案] C
eq \a\vs4\al()
判断集合间关系的常用方法

[跟踪训练]
1．(多选)下列关系中，正确的有( )
A．0∈{0} B．∅{0}
C．{0，1}{(0，1)} D．{(1，2)}＝{(2，1)}
解析：选AB 对于A，集合{0}中含有1个元素0，所以0∈{0}正确；对于B，由于空集是任何非空集合的真子集，所以∅{0}正确；对于C，{0，1}是数集，{(0，1)}是点集，所以C错误；对于D，{(1，2)}与{(2，1)}是不同的点集，所以D错误．
2．已知集合A＝{x|x2－3x＋2＝0}，B＝{1，2}，C＝{x|x<8，x∈N}，用适当的符号填空：
(1)A________B；(2)A________C；
(3){2}________C；(4)2________C.
解析：集合A为方程x2－3x＋2＝0的解集，即A＝{1，2}，而C＝{x|x<8，x∈N}＝{0，1，2，3，4，5，6，7}．故(1)A＝B；(2)AC；(3){2}C；(4)2∈C.
答案：(1)＝ (2) (3) (4)∈
[例2] (链接教科书第7页例4)(1)已知集合A＝{(x，y)|4x＋3y－12＜0，x∈N＋，y∈N＋}，则集合A的子集的个数为( )
A．3 B．4
C．7 D．8
(2)(2020·北京海淀区月考)已知集合M满足{1，2}M⊆{1，2，3，4，5}，则所有满足条件的集合M的个数是( )
A．6 B．7
C．8 D．9
[解析] (1)用列举法表示集合A，得A＝{(1，1)，(1，2)，(2，1)}，则集合A的子集的个数为23＝8.
(2)由题意可以确定集合M必含有元素1，2，且至少含有元素3，4，5中的一个，因此依据集合M的元素个数分类如下．
含有3个元素：{1，2，3}，{1，2，4}，{1，2，5}．
含有4个元素：{1，2，3，4}，{1，2，3，5}，{1，2，4，5}．
含有5个元素：{1，2，3，4，5}．
故满足条件的集合M为{1，2，3}，{1，2，4}，{1，2，5}，{1，2，3，4}，{1，2，3，5}，{1，2，4，5}，{1，2，3，4，5}．
[答案] (1)D (2)B
eq \a\vs4\al()
求集合子集、真子集个数的3个步骤

[跟踪训练]
已知集合A＝{－1，0，1}，则含有元素0的A的子集的个数为( )
A．2 B．4
C．6 D．8
解析：选B 根据题意，含有元素0的A的子集为{0}，{0，1}，{0，－1}，{－1，0，1}，共4个.
[例3] 已知集合A＝{x|－2≤x≤5}，B＝{x|m－6≤x≤2m－1}，若A⊆B，求实数m的取值范围．
[解] ∵A⊆B，
∴eq \b\lc\{(\a\vs4\al\c1(2m－1＞m－6，,m－6≤－2，,2m－1≥5，))解得eq \b\lc\{(\a\vs4\al\c1(m＞－5，,m≤4，,m≥3，))故3≤m≤4.
∴实数m的取值范围是{m|3≤m≤4}．
[母题探究]
1．(变条件)本例中若将“A⊆B”改为“B⊆A”，其他条件不变，求m的取值范围．
解：当B＝∅时，m－6＞2m－1，即m＜－5.
当B≠∅时，eq \b\lc\{(\a\vs4\al\c1(m－6≤2m－1，,m－6≥－2，,2m－1≤5，))eq \b\lc\{(\a\vs4\al\c1(m≥－5，,m≥4，,m≤3，))
即m∈∅.
故实数m的取值范围是{m|m＜－5}．
2．(变条件，变设问)本例若将集合A，B分别改为A＝{－1，3，2m－1}，B＝{3，m2}，且B⊆A，则实数m的值又是什么？
解：因为B⊆A，所以m2＝2m－1，即(m－1)2＝0，所以m＝1，当m＝1时，A＝{－1，3，1}，B＝{3，1}，满足B⊆A.所以m的值为1.
eq \a\vs4\al()
由集合间的包含关系求参数的方法
(1)当集合为不连续数集时，常根据集合包含关系的意义，建立方程求解，此时应注意分类讨论；
(2)当集合为连续数集时，常借助数轴来建立不等关系求解，应注意端点处是实点还是虚点．
[提醒] (1)不能忽视集合为∅的情形；
(2)当集合中含有字母参数时，一般要分类讨论．
[跟踪训练]
已知集合M＝{x|x2＋2x－a＝0}．
(1)若∅M，求实数a的取值范围；
(2)若N＝{x|x2＋x＝0}且M⊆N，求实数a的取值范围．
解：(1)由题意得，方程x2＋2x－a＝0有实数解，
∴Δ＝22－4×(－a)≥0，得a≥－1，
即实数a的取值范围为[－1，＋∞)．
(2)∵N＝{x|x2＋x＝0}＝{0，－1}，且M⊆N，
∴当M＝∅时，Δ＝22－4×(－a)＜0，得a＜－1；
当M≠∅时，当Δ＝0时，a＝－1，
此时M＝{－1}，满足M⊆N，符合题意．
当Δ＞0时，a＞－1，M中有两个元素，
若M⊆N，则M＝N，从而eq \b\lc\{(\a\vs4\al\c1(－1＋0＝－2，,（－1）×0＝－a，))无解．
综上，实数a的取值范围为(－∞，－1]．
子集个数的探究
观察下表并回答后面的问题.
[问题探究]
1．若集合A有n个元素，则集合A有多少个子集？多少个真子集？多少个非空真子集？
提示：若集合A含有n个元素，则集合A有2n个子集；其真子集要去掉集合A本身，故有2n－1个；非空真子集要去掉集合A本身与空集，故有2n－2个．
2．对于有限集A，B，C，设集合A中含有n个元素，集合B中有m个元素(n，m∈N，且n>m)．
(1)当B⊆C⊆A时，满足条件的C有多少个？
(2)如果集合C分别满足如下条件：B⊆CA，BC⊆A，BCA，那么C的个数为多少？
提示：(1)由表格中的集合可知，若B⊆C⊆A，则集合C中一定有集合B的全部元素，也就是A中元素去掉B中元素后剩余元素构成的集合的子集，故有2n－m个．
(2)①当B⊆CA时，在问题(1)的基础上，去掉与集合A相等的集合，故满足条件的C有2n－m－1个．
②当BC⊆A时，在问题(1)的基础上，去掉与集合B相等的集合，故满足条件的C有2n－m－1个．
③当BCA时，在问题(1)的基础上，去掉与集合A，B相等的两个集合，故有2n－m－2个．
[迁移应用]
1．已知M为非空数集，M⊆{1，2，3}，且M中至少有一个元素是奇数，则这样的集合M共有( )
A．6个 B．5个
C．4个 D．3个
解析：选A 集合{1，2，3}的子集共有23＝8(个)，集合{2}的子集共有2个，所以满足要求的集合M共有8－2＝6(个)．故选A.
2．设集合Sn＝{1，2，3，…，n}，若X是Sn的子集，我们把X中所有无素的和称为X的容量(规定空集的容量为0)，若X的容量为奇(偶)数，则称X为Sn的奇(偶)子集．则S4的所有奇子集有________个．
解析：因为S4＝{1，2，3，4}，所以S4的所有奇子集为{1}，{3}，{1，2}，{1，4}，{2，3}，{3，4}，{1，2，4}，{2，3，4}，共有8个．
答案：8
1．下列各组两个集合A和B，表示相等集合的是( )
A．A＝{π}，B＝{3.141 59}
B．A＝{2，3}，B＝{(2，3)}
C．A＝{1，eq \r(3)，π}，B＝{π，1，|－eq \r(3)|}
D．A＝{x|－1＜x≤1，x∈N}，B＝{1}
解析：选C 集合相等，两集合中的元素完全相同．
选项A，∵π≠3.141 59，∴A≠B；
选项B，∵2，3表示两个实数，而(2，3)表示一个点，
∴A≠B；
选项C，∵|－eq \r(3)|＝eq \r(3)，∴A＝B；
选项D，∵A＝{x|－1＜x≤1，x∈N}＝{0，1}≠B＝{1}，∴A≠B.
2．(2021·温州高一月考)已知集合P＝{－1，0，1，2}，Q＝{－1，0，1}，则( )
A．P∈Q B．P⊆Q
C．Q⊆P D．Q∈P
解析：选C 集合P＝{－1，0，1，2}，Q＝{－1，0，1}，因为集合Q中的元素都在集合P中，所以Q⊆P.故选C.
3．(多选)已知集合A＝{x|x2－9＝0}，则下列式子表示正确的有( )
A．3∈A B．{－3}∈A
C．∅⊆A D．{3，－3}⊆A
解析：选ACD 根据题意知，集合A＝{x|x2－9＝0}＝{－3，3}，依次分析4个式子：对于A，3∈A，3是集合A的元素，正确；对于B，{－3}∈A，{－3}是集合，应有{－3}⊆A，错误；对于C，∅⊆A，空集是任何集合的子集，正确；对于D，{3，－3}⊆A，任何集合都是其本身的子集，正确．
4．已知集合A＝{－1，3，m}，B＝{3，4}，若B⊆A，则实数m＝________．
解析：∵B⊆A，∴元素3，4必为A中元素，∴m＝4.
答案：4
5．集合A＝{x|x≥1，或x≤－2}，B＝{x|x≥a}，若BA，则实数a的取值范围是________．
解析：如图，eq \a\vs4\al()，若BA，则a≥1.
答案：[1，＋∞)
新课程标准解读
核心素养
1.理解集合之间包含与相等的含义，能识别给定集合的子集
数学抽象、逻辑推理
2.在具体情境中，了解空集的含义
数学抽象
3.能使用Venn图表达集合的基本关系，体会图形对理解抽象概念的作用
数学抽象、直观想象
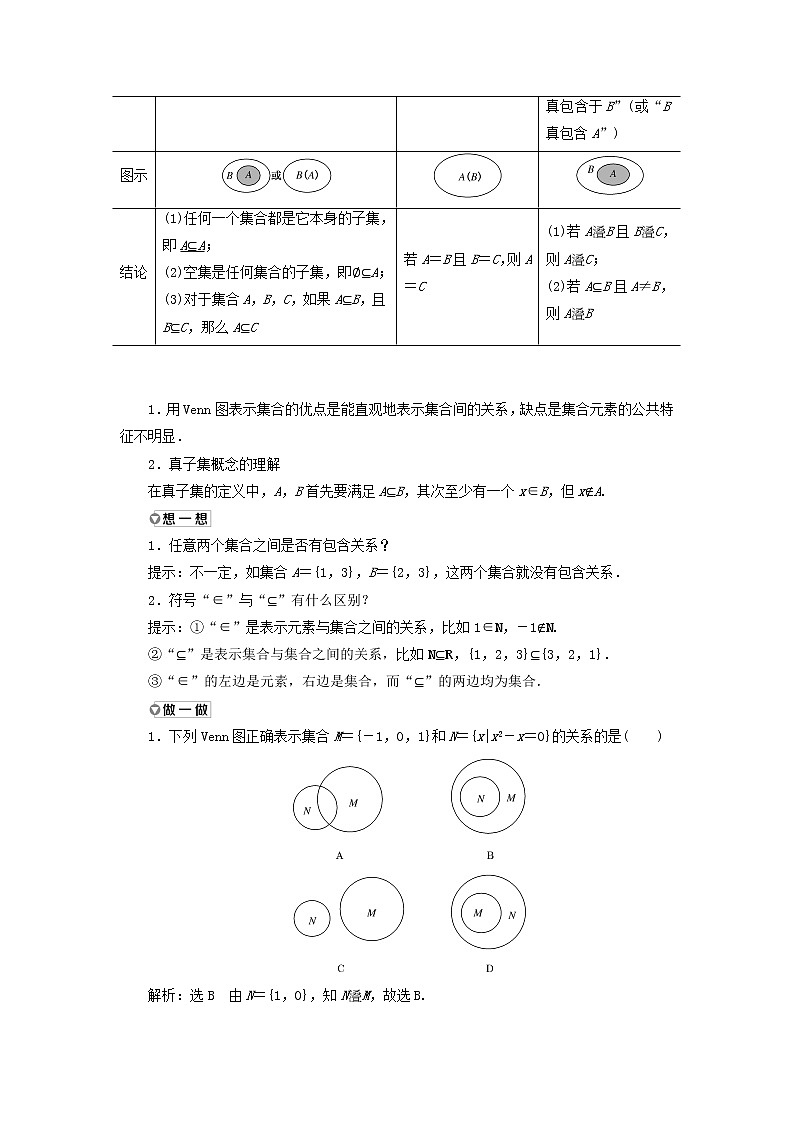
子集
集合相等
真子集
概念
一般地，对于两个集合A与B，如果集合A中的任何一个元素都属于集合B，即若a∈A，则a∈B，那么称集合A是集合B的子集，记作A⊆B(或B⊇A)，读作“A包含于B”(或“B包含A”)
如果集合A是集合B的子集，且集合B也是集合A的子集，那么称集合A与集合B相等，记作A＝B
对于两个集合A与B，如果A⊆B，且A≠B，那么称集合A是集合B的真子集，记作AB(或BA)，读作“A真包含于B”(或“B真包含A”)
图示
结论
(1)任何一个集合都是它本身的子集，即A⊆A；
(2)空集是任何集合的子集，即∅⊆A；
(3)对于集合A，B，C，如果A⊆B，且B⊆C，那么A⊆C
若A＝B且B＝C，则A＝C
(1)若AB且BC，则AC；
(2)若A⊆B且A≠B，则AB
集合间关系判断
确定有限集合的子集、真子集及其个数
由集合间的关系求参数值(或范围)
集合B
集合A
关系
集合C的所有子集
集合C的个数
{a}
{a，b}
B⊆C⊆A
{a}，{a，b}
2
{a}
{a，b，c}
B⊆C⊆A
{a}，{a，b}，{a，c}，{a，b，c}
4
{a}
{a，b，c，d}
B⊆C⊆A
{a}，{a，b}，{a，c}，{a，d}，{a，b，c}，{a，b，d}，{a，c，d}，{a，b，c，d}
8