

人教版数学 八年级(下)第一次月考试卷(有答案)
展开
这是一份人教版数学 八年级(下)第一次月考试卷(有答案),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2021-2022学年八年级(下)第一次月考数学试卷
一、选择题(每题4分,共64分)
1.下列二次根式与是同类二次根式的是( )
A. B. C.﹣ D.
2.下列运算中正确的是( )
A.+= B.(4+3)×=8+6
C.÷=1 D.(+)(﹣)=1
3.能使有意义的x的取值范围是( )
A.x>﹣2 B.x≥﹣2 C.x>0 D.x≥﹣2且x≠0
4.在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
A. B. C. D.
5.在平面直角坐标系中,将函数y=3x的图象向上平移6个单位长度,则平移后的图象与x轴的交点坐标为( )
A.(2,0) B.(﹣2,0) C.(6,0) D.(﹣6,0)
6.已知点M(1,a)、N(﹣2,b)是一次函数y=﹣2x+1图象上的两点,则a与b的大小关系是( )
A.a>b B.a=b C.a<b D.以上都不对
7.若ab<0且a>b,则函数y=ax+b的图象可能是( )
A. B.
C. D.
8.关于▱ABCD的叙述,正确的是( )
A.若AB⊥BC,则▱ABCD是菱形
B.若AC⊥BD,则▱ABCD是正方形
C.若AC=BD,则▱ABCD是矩形
D.若AB=AD,则▱ABCD是正方形
9.如图,直线y=kx+b(k≠0)经过点A(﹣2,4),则不等式kx+b>4的解集为( )
A.x>﹣2 B.x<﹣2 C.x>4 D.x<4
10.如图,D、E分别为△ABC中AB、AC边上的中点,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为( )
A.1 B. C.2 D.
11.如图,矩形ABCD中,AB=4cm,BC=8cm,如果将该矩形沿对角线BD折叠,那么图中阴影部分的面积( )cm2.
A.8 B.10 C.15 D.20
12.如图,已知▱ABCD与正方形CEFG,其中E点在AD上.若∠ECD=35°,∠AEF=15°,则∠B的度数是( )
A.75° B.70° C.55° D.50°
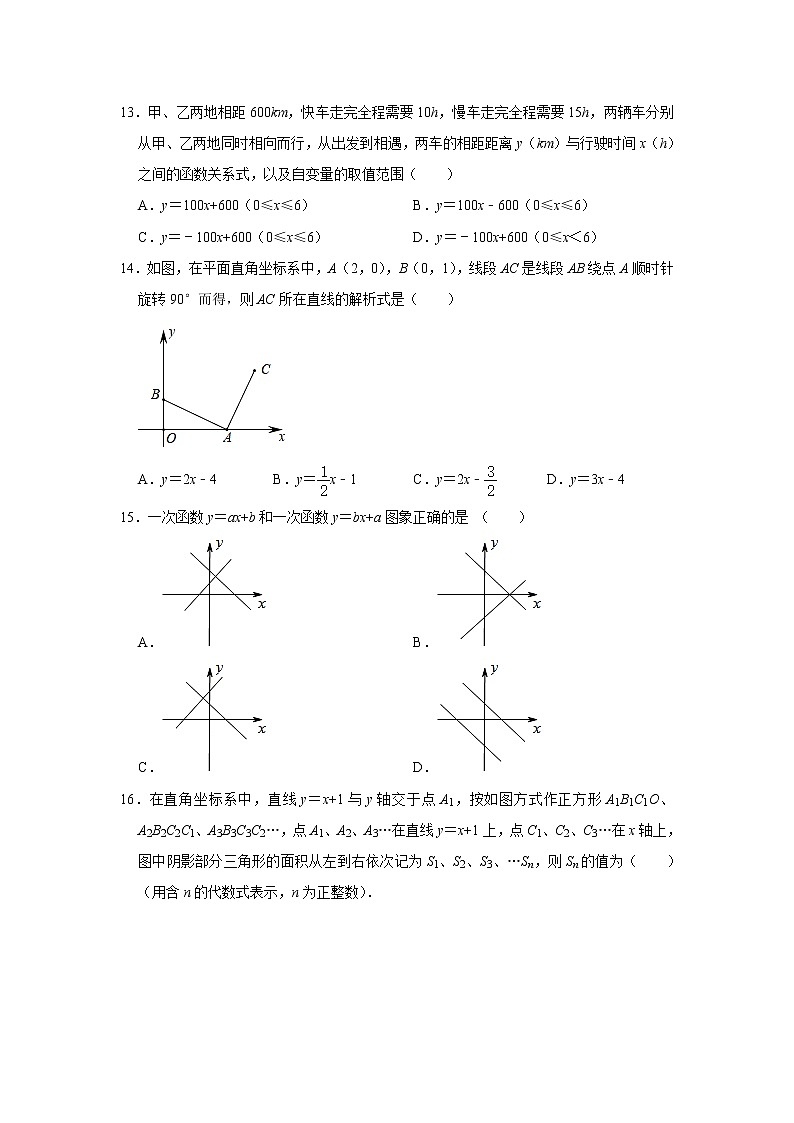
13.甲、乙两地相距600km,快车走完全程需要10h,慢车走完全程需要15h,两辆车分别从甲、乙两地同时相向而行,从出发到相遇,两车的相距距离y(km)与行驶时间x(h)之间的函数关系式,以及自变量的取值范围( )
A.y=100x+600(0≤x≤6) B.y=100x﹣600(0≤x≤6)
C.y=﹣100x+600(0≤x≤6) D.y=﹣100x+600(0≤x<6)
14.如图,在平面直角坐标系中,A(2,0),B(0,1),线段AC是线段AB绕点A顺时针旋转90°而得,则AC所在直线的解析式是( )
A.y=2x﹣4 B.y=x﹣1 C.y=2x﹣ D.y=3x﹣4
15.一次函数y=ax+b和一次函数y=bx+a图象正确的是 ( )
A. B.
C. D.
16.在直角坐标系中,直线y=x+1与y轴交于点A1,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C3C2…,点A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左到右依次记为S1、S2、S3、…Sn,则Sn的值为( )(用含n的代数式表示,n为正整数).
A.n2 B.22n﹣3 C. D.
二、填空题(共12分)
17.(12分)已知函数y=(1﹣m)x+2m+2,试解决下列问题:
(1)当m≠ 时,该函数是一次函数;
(2)当m=2时,函数图象不经过第 象限;
(3)当函数y=(1﹣m)x+2m+2向上平移4个单位长度时,得到y=(1﹣m)x+2,则m的值为 ;
(4)若函数图象与x轴交于点A,与y轴的交点坐标为B(0,6),则△ABO的面积为 ;
(5)无论m取何值,该函数图象都经过一个定点,则这个定点的横坐标是 ,纵坐标是 .
三、解答题(共24分)
18.(12分)计算:
(1)(+)÷;
(2)﹣(π)0+÷;
(3)(2+)(2﹣)﹣+()﹣1.
19.(12分)如图,正方形ABCD的边长为3,BC边在x轴上,BC的中点与原点O重合,过定点M(﹣2,0)与动点P(0,t)的直线MP记作l.
(1)A点坐标为 ,D点坐标为 ;
(2)若l的解析式为y=2x+4,判断此时点A是否在直线l上,并说明理由;
(3)当直线l与AD边有公共点时,求t的取值范围.
参考答案与试题解析
一、选择题(每题4分,共64分)
1.下列二次根式与是同类二次根式的是( )
A. B. C.﹣ D.
【分析】根据二次根式的性质把各个二次根式化简,根据同类二次根式的概念判断即可.
【解答】解:A、==3,与不是同类二次根式;
B、==,与不是同类二次根式;
C、﹣=﹣2,与是同类二次根式;
D、==6,与不是同类二次根式;
故选:C.
2.下列运算中正确的是( )
A.+= B.(4+3)×=8+6
C.÷=1 D.(+)(﹣)=1
【分析】利用二次根式的加减法对A进行判断;利用二次根式的乘法法则对B进行判断;利用二次根式的除法法则对C进行判断;利用平方差公式对D进行判断.
【解答】解:A、原式=+2,所以A选项错误;
B、原式=8+6,所以B选项正确;
C、原式==3,所以C选项错误;
D、原式=6﹣7=1,所以D选项错误.
故选:B.
3.能使有意义的x的取值范围是( )
A.x>﹣2 B.x≥﹣2 C.x>0 D.x≥﹣2且x≠0
【分析】让二次根式的被开方数大于或等于0,分母不为0,列不等式求解即可.
【解答】解:由题意得:x+2≥0,且x≠0;
解得:x≥﹣2且x≠0,
故选:D.
4.在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
A. B. C. D.
【分析】根据题意画出相应的图形,如图所示,在直角三角形ABC中,由AC及BC的长,利用勾股定理求出AB的长,然后过C作CD垂直于AB,由直角三角形的面积可以由两直角边乘积的一半来求,也可以由斜边AB乘以斜边上的高CD除以2来求,两者相等,将AC,AB及BC的长代入求出CD的长,即为C到AB的距离.
【解答】解:根据题意画出相应的图形,如图所示:
在Rt△ABC中,AC=9,BC=12,
根据勾股定理得:AB==15,
过C作CD⊥AB,交AB于点D,
又S△ABC=AC•BC=AB•CD,
∴CD===,
则点C到AB的距离是.
故选:A.
5.在平面直角坐标系中,将函数y=3x的图象向上平移6个单位长度,则平移后的图象与x轴的交点坐标为( )
A.(2,0) B.(﹣2,0) C.(6,0) D.(﹣6,0)
【分析】根据“上加下减”的原则求得平移后的解析式,令y=0,解得即可.
【解答】解:由“上加下减”的原则可知,将函数y=3x的图象向上平移6个单位长度所得函数的解析式为y=3x+6,
∵此时与x轴相交,则y=0,
∴3x+6=0,即x=﹣2,
∴点坐标为(﹣2,0),
故选:B.
6.已知点M(1,a)、N(﹣2,b)是一次函数y=﹣2x+1图象上的两点,则a与b的大小关系是( )
A.a>b B.a=b C.a<b D.以上都不对
【分析】根据一次函数中k的值确定函数的增减性,然后比较a、b的大小即可.
【解答】解:∵关于x的一次函数y=﹣2x+1中的k=﹣2<0,
∴y随x的增大而减小,
∵图象经过(1,a)、(2,b)两点,且﹣2<1,
∴a<b,
故选:C.
7.若ab<0且a>b,则函数y=ax+b的图象可能是( )
A. B.
C. D.
【分析】利用ab<0,且a>b得到a>0,b<0,然后根据一次函数图象与系数的关系进行判断.
【解答】解:∵ab<0,且a>b,
∴a>0,b<0,
∴函数y=ax+b的图象经过第一、三、四象限.
故选:A.
8.关于▱ABCD的叙述,正确的是( )
A.若AB⊥BC,则▱ABCD是菱形
B.若AC⊥BD,则▱ABCD是正方形
C.若AC=BD,则▱ABCD是矩形
D.若AB=AD,则▱ABCD是正方形
【分析】由菱形的判定方法、矩形的判定方法、正方形的判定方法得出选项A、B、D错误,C正确;即可得出结论.
【解答】解:∵▱ABCD中,AB⊥BC,
∴四边形ABCD是矩形,不一定是菱形,选项A错误;
∵▱ABCD中,AC⊥BD,
∴四边形ABCD是菱形,不一定是正方形,选项B错误;
∵▱ABCD中,AC=BD,
∴四边形ABCD是矩形,选项C正确;
∵▱ABCD中,AB=AD,
∴四边形ABCD是菱形,不一定是正方形,选项D错误.
故选:C.
9.如图,直线y=kx+b(k≠0)经过点A(﹣2,4),则不等式kx+b>4的解集为( )
A.x>﹣2 B.x<﹣2 C.x>4 D.x<4
【分析】结合函数的图象利用数形结合的方法确定不等式的解集即可.
【解答】解:观察图象知:当x>﹣2时,kx+b>4,
故选:A.
10.如图,D、E分别为△ABC中AB、AC边上的中点,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为( )
A.1 B. C.2 D.
【分析】根据勾股定理求出DE,根据直角三角形的性质求出DF,结合图形计算,得到答案.
【解答】解:∵D、E分别为△ABC中AB、AC边上的中点,
∴DE是△ABC的中位线,
∴DE=BC=4,
在Rt△AFB中,D是AB的中点,
∴DF=AB=,
∴EF=DE﹣DF=,
故选:B.
11.如图,矩形ABCD中,AB=4cm,BC=8cm,如果将该矩形沿对角线BD折叠,那么图中阴影部分的面积( )cm2.
A.8 B.10 C.15 D.20
【分析】易得BE=DE,利用勾股定理求得DE的长,利用三角形的面积公式可得阴影部分的面积.
【解答】解:根据翻折的性质可知:∠EBD=∠DBC,
又∵AD∥BC,
∴∠ADB=∠DBC,
∴∠ADB=∠EBD,
∴BE=DE,
设BE=DE=x,
∴AE=8﹣x,
∵四边形ABCD是矩形,
∴∠A=90°,
∴AE2+AB2=BE2,
(8﹣x)2+42=x2,
解得x=5,
∴S△EDB=×5×4=10.
故选:B.
12.如图,已知▱ABCD与正方形CEFG,其中E点在AD上.若∠ECD=35°,∠AEF=15°,则∠B的度数是( )
A.75° B.70° C.55° D.50°
【分析】由平角的定义求出∠CED的度数,由三角形内角和定理求出∠D的度数,再由平行四边形的对角相等即可得出结果.
【解答】解:∵四边形CEFG是正方形,
∴∠CEF=90°,
∵∠CED=180°﹣∠AEF﹣∠CEF=180°﹣15°﹣90°=75°,
∴∠D=180°﹣∠CED﹣∠ECD=180°﹣75°﹣35°=70°,
∵四边形ABCD为平行四边形,
∴∠B=∠D=70°.
故选:B.
13.甲、乙两地相距600km,快车走完全程需要10h,慢车走完全程需要15h,两辆车分别从甲、乙两地同时相向而行,从出发到相遇,两车的相距距离y(km)与行驶时间x(h)之间的函数关系式,以及自变量的取值范围( )
A.y=100x+600(0≤x≤6) B.y=100x﹣600(0≤x≤6)
C.y=﹣100x+600(0≤x≤6) D.y=﹣100x+600(0≤x<6)
【分析】由“路程÷时间=速度”求得快车、慢车的行驶速度;然后根据两车间的距离=总距离﹣甲、乙两车行驶的距离,据此可得两车的相距距离y(km)与行驶时间x(h)之间的函数关系式,以及自变量的取值范围.
【解答】解:快车的速度是600÷10=60(km/h),慢车的速度是600÷15=40(km/h),
由行程问题,得y=﹣(60+40)x+600=﹣100x+600(0≤x≤6).
故选:C.
14.如图,在平面直角坐标系中,A(2,0),B(0,1),线段AC是线段AB绕点A顺时针旋转90°而得,则AC所在直线的解析式是( )
A.y=2x﹣4 B.y=x﹣1 C.y=2x﹣ D.y=3x﹣4
【分析】过点C作CD⊥x轴于点D,易知△ACD≌△BAO(AAS),从而求得点C坐标,设直线AC的解析式为y=kx+b,将点A,点C坐标代入求得k和b,从而得解.
【解答】解:∵A(2,0),B(0,1)
∴OA=2,OB=1
过点C作CD⊥x轴于点D,
则∠AOB=∠CDA=90°,
∵∠BAC=90°,
∴∠BAO=∠ACD=90°﹣∠CAD,
∵BA=AC,
∴△ACD≌△BAO(AAS),
∴AD=OB=1,CD=OA=2,
∴C(3,2),
设直线AC的解析式为y=kx+b,将点A,点C坐标代入得:
,
解得:,
∴直线AC的解析式为y=2x﹣4,
故选:A.
15.一次函数y=ax+b和一次函数y=bx+a图象正确的是 ( )
A. B.
C. D.
【分析】本题可先确定一次函数y=ax+b的字母系数的正负,再判断函数y=bx+a的字母系数的正负,从而得到答案.
【解答】解;设a>0,b<0,则函数y=ax+b的图象是上升的,交y轴的负半轴,函数y=bx+a图象是下降的,与y轴交于正半轴,
设a<0,b>0,则函数y=ax+b的图象是下降的,交y轴的正半轴,函数y=bx+a图象是上升的,与y轴交于负半轴,
设a>0,b>0,则函数y=ax+b的图象是上升的,交y轴的正半轴,函数y=bx+a图象是上升的,与y轴交于正半轴,
设a<0,b<0,则函数y=ax+b的图象是下降的,交y轴的负半轴,函数y=bx+a图象是下降的,与y轴交于负半轴,
故选:B.
16.在直角坐标系中,直线y=x+1与y轴交于点A1,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C3C2…,点A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左到右依次记为S1、S2、S3、…Sn,则Sn的值为( )(用含n的代数式表示,n为正整数).
A.n2 B.22n﹣3 C. D.
【分析】根据直线解析式判断出直线与坐标轴相交构成的三角形是等腰直角三角形,再求出OA1,即第一个正方形的边长,同理依次求出第二个、第三个正方形的边长,然后根据规律写出第n个正方形的边长,如果根据阴影部分的面积等于相应正方形的面积的一半列式计算即可得解.
【解答】解:∵直线y=x+1的k=1,
∴直线与x轴的夹角为45°,
∴直线与坐标轴相交构成的三角形是等腰直角三角形,
当x=0时,y=1,
所以,OA1=1,
即第一个正方形的边长为1,
所以,第二个正方形的边长为1+1=2,
第三个正方形的边长为2+2=4=22,
…,
第n个正方形的边长为2n﹣1,
∴S1=×1×1=,
S2=×2×2=,
S3=×22×22=,
…,
Sn=×2n﹣1×2n﹣1==22n﹣3.
故选:B.
二、填空题(共12分)
17.(12分)已知函数y=(1﹣m)x+2m+2,试解决下列问题:
(1)当m≠ 1 时,该函数是一次函数;
(2)当m=2时,函数图象不经过第 三 象限;
(3)当函数y=(1﹣m)x+2m+2向上平移4个单位长度时,得到y=(1﹣m)x+2,则m的值为 ﹣2 ;
(4)若函数图象与x轴交于点A,与y轴的交点坐标为B(0,6),则△ABO的面积为 18 ;
(5)无论m取何值,该函数图象都经过一个定点,则这个定点的横坐标是 2 ,纵坐标是 4 .
【分析】(1)直接利用一次函数的定义得出答案;
(2)根据一次函数的性质即可得到结论;
(3)根据平移的性质得方程,于是得到结论;
(4)根据题意得到方程,解方程得到A点的坐标,然后根据三角形的面积公式即可得到结论;
(5)先把解析式变形为关于m的不定方程,根据不定方程的解的情况得到结论.
【解答】解:(1)∵函数y=(1﹣m)x+2m+2,
∴当m﹣1≠0时,该函数是一次函数,即m≠1;
(2)当m=2时,函数y=(1﹣m)x+2m+2为y=﹣x+6,
解:∵k=﹣1<0,
∴一次函数经过二四象限;
∵b>0,
∴一次函数又经过第一象限,
∴一次函数y=﹣x+6的图象不经过第三象限;
(3)根据题意得,2m+2+4=2,
解得:m=﹣2;
(4)∵y=(1﹣m)x+2m+2与y轴的交点坐标为B(0,6),
∴2m+2=6,
∴m=2,
∴y=﹣x+6,
令y=0,
∴x=6,
∴A(6,0),
∴△ABO的面积为=18;
(5)∵y=(1﹣m)x+2m+2,
∴(x﹣2)m=x+2﹣y,
∵m可取任意值,
∴x﹣2=0,x+2﹣y=0,解得x=2,y=4,
∴函数函数y=(1﹣m)x+2m+2的图象经过一个定点(2,4).
∴这个定点的横坐标是2,纵坐标是4.
故答案为:(1)1;(2)三;(3)﹣2;(4)18;(5)2,4.
三、解答题(共24分)
18.(12分)计算:
(1)(+)÷;
(2)﹣(π)0+÷;
(3)(2+)(2﹣)﹣+()﹣1.
【分析】(1)先把二次根式化为最简二次根式和除法运算化为乘法运算,然后进行二次根式的乘法运算;
(2)利用零指数幂的意义和二次根式的除法法则运算即可.
(3)利用二次根式的性质、平方差公式和负整数指数幂的意义计算.
【解答】解:(1)原式=(4+)×
=5×
=5;
(2)原式=3﹣1+
=3﹣1+2
=5﹣1;
(3)原式=4﹣5﹣(2﹣3)+
=4﹣5﹣2+3+
=2﹣.
19.(12分)如图,正方形ABCD的边长为3,BC边在x轴上,BC的中点与原点O重合,过定点M(﹣2,0)与动点P(0,t)的直线MP记作l.
(1)A点坐标为 (﹣,3) ,D点坐标为 (,3) ;
(2)若l的解析式为y=2x+4,判断此时点A是否在直线l上,并说明理由;
(3)当直线l与AD边有公共点时,求t的取值范围.
【分析】(1)BC的中点与原点O重合,则点B、C的坐标分别为(﹣,0)、(,0),进而求解;
(2)当x=﹣时,y=2x+4=2×(﹣)+4=1≠3,即可求解;
(3)求出直线l的表达式,求出点A、D为临界点时t的值即可求解.
【解答】解:(1)∵BC的中点与原点O重合,则点B、C的坐标分别为(﹣,0)、(,0),
则点A、D的坐标分别为(﹣,3)、(,3),
故答案为:(﹣,3)、(,3);
(2)当x=﹣时,y=2x+4=2×(﹣)+4=1≠3,
故点A不在直线l上;
(3)直线l过点P,则设直线l的表达式为y=kx+t,
将点M的坐标代入上式得:0=﹣2k+t,解得k=t,
则直线l的表达式为y=tx+t,
当直线l过点A时,则3=﹣×t+t=t,解得t=12,
当直线l过点D时,则3=t×+t=,解得t=,
故≤t≤12.
相关试卷
这是一份人教版数学 八年级(下)第一次月考试卷(有答案),共27页。试卷主要包含了解答题等内容,欢迎下载使用。
这是一份人教版数学 八年级(下)第一次月考试卷(有答案),共5页。
这是一份人教版数学 八年级(下)第一次月考试卷(有答案),共6页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。









