人教版数学 八年级（下）第一次月考试卷（有答案）

这是一份人教版数学 八年级（下）第一次月考试卷（有答案），共5页。
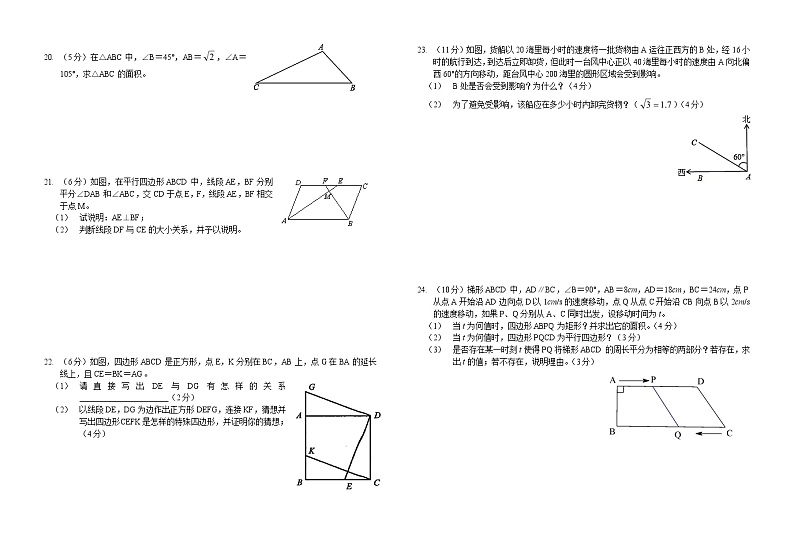
人教版2021-2022年度初二（下）第一次月考数学试卷一、     选择题（每题3分，共36分）下列各式中，是最简二次根式的是（    ）A.    B.    C.    D. 下列说法正确的是（    ）A. 若，则  B. 若，则 C.     D. 5的平方根是在下列以线段a，b，c的长为三边的三角形中，不能构成直角三角形的是（    ）A. a＝11，b＝12，c＝15  B. a＝b＝5，c＝  C. a：b：c＝1：1：  D. a＝1，b＝，c＝2下列说法正确的是（    ）A. 真命题的逆命题是真命题 B. 原命题是假命题，则它的逆命题也是假命题C. 命题一定有逆命题   D. 定理一定有逆定理四边形ABCD的对角线AC、BD交于点O，能判断它是正方形的是（    ）A. AO＝OC，OB＝OD    B. AO＝BO＝CO＝DO，AC⊥BD    C. AO＝OC，OB＝OD，AC⊥BD  D.  AO＝OC＝OB＝OD 下列不是函数图象的是（    ）A．B.C. D. 如图，点A表示的实数是（    ）A.   B.   C.   D. 如图，已知矩形ABCD沿着直线BD折叠，使点C落在C＇处，B C＇交AD于E，AD＝8，AB＝4，则DE的长为（    ）A. 3    B. 4    C. 5   D. 6若一个三角形的三边长为3、4、x，则使此三角形是直角三角形的x的值是（    ）A.  5  B. 6   C.   D. 5或如图，已知E是菱形ABCD的边BC上一点，且∠DAE＝∠B＝80°，那么∠CDE的度数为（    ）A. 20°  B.  25°  C.  30°  D.  35° 平行四边形的一边的长为10cm，则这个平行四边形的两条对角线的长可以是（    ）A. 4cm，6cm  B. 6cm，8cm   C. 8cm，10cm   D. 10cm，12cm如图，在平行四边形ABCD中，剪去大小不同的平行四边形EGFC，得到另两个图形，三个图形分别标上（L）、（M）、（N），记周长分别为l、m、n，则必有（    ）                 B.   C.   D. 无法确定 二、     填空题（每小题4分，共24分）函数的自变量取值范围是________。如图，斜折一页书的一角，使点A落在同一页书内的A＇处，DE为折痕，作DF平分∠A＇DB，则∠FDE＝________°。菱形ABCD中，∠A＝60°，对角线BD长为7cm，则此菱形周长________cm。将一根长24cm的筷子，置于底面直径为5cm，高为12cm的圆柱形水杯中，设筷子露在杯子外面的长度为hcm，则h的最小值是________cm。一个平行四边形的周长为70cm，两边的差是9cm，则平行四边形较大边长为_______cm。实数a在数轴上的位置如图所示，化简_________。三、     解答题（本大题共6小题，共66分。解答应写出文字说明、演算步骤或推理过程）（5分）先化简，再求值：，其中。     （5分）在△ABC中，∠B＝45°，AB＝，∠A＝105°，求△ABC的面积。        （6分）如图，在平行四边形ABCD中，线段AE，BF分别平分∠DAB和∠ABC，交CD于点E，F，线段AE，BF相交于点M。（1）          试说明：AE⊥BF；（2）          判断线段DF与CE的大小关系，并予以说明。          （6分）如图，四边形ABCD是正方形，点E，K分别在BC，AB上，点G在BA的延长线上，且CE＝BK＝AG。（1）          请直接写出DE与DG有怎样的关系______________________（2分）（2）          以线段DE，DG为边作出正方形DEFG，连接KF，猜想并写出四边形CEFK是怎样的特殊四边形，并证明你的猜想；（4分）      （11分）如图，货船以20海里每小时的速度将一批货物由A运往正西方的B处，经16小时的航行到达，到达后立即卸货，但此时一台风中心正以40海里每小时的速度由A向北偏西60°的方向移动，距台风中心200海里的圆形区域会受到影响。（1）          B处是否会受到影响？为什么？（4分）（2）          为了避免受影响，该船应在多少小时内卸完货物？（）（4分）             （10分）梯形ABCD中，AD∥BC，∠B＝90°，AB＝8cm，AD＝18cm，BC＝24cm，点P从点A开始沿AD边向点D以1cm/s的速度移动，点Q从点C开始沿CB向点B以2cm/s的速度移动，如果P、Q分别从A、C同时出发，设移动时间为t。（1）          当t为何值时，四边形ABPQ为矩形？并求出它的面积。（4分）（2）          当t为何值时，四边形PQCD为平行四边形？（3分）（3）          是否存在某一时刻t使得PQ将梯形ABCD的周长平分为相等的两部分？若存在，求出t的值；若不存在，说明理由。（3分）           试卷答案一、     选择题（每题3分，共36分）下列各式中，是最简二次根式的是（ C ）A.    B.    C.    D. 下列说法正确的是（ B ）A. 若，则  B. 若，则 C.     D. 5的平方根是在下列以线段a，b，c的长为三边的三角形中，不能构成直角三角形的是（ A ）A. a＝11，b＝12，c＝15  B. a＝b＝5，c＝  C. a：b：c＝1：1：  D. a＝1，b＝，c＝2下列说法正确的是（ C ）A. 真命题的逆命题是真命题 B. 原命题是假命题，则它的逆命题也是假命题C. 命题一定有逆命题   D. 定理一定有逆定理四边形ABCD的对角线AC、BD交于点O，能判断它是正方形的是（ B ）A. AO＝OC，OB＝OD    B. AO＝BO＝CO＝DO，AC⊥BD    C. AO＝OC，OB＝OD，AC⊥BD  D.  AO＝OC＝OB＝OD 下列不是函数图象的是（ D ）A．B.C. D. 如图，点A表示的实数是（ C ）A.   B.   C.   D. 如图，已知矩形ABCD沿着直线BD折叠，使点C落在C＇处，B C＇交AD于E，AD＝8，AB＝4，则DE的长为（ C ）A. 3    B. 4    C. 5   D. 6若一个三角形的三边长为3、4、x，则使此三角形是直角三角形的x的值是（ D ）A.  5  B. 6   C.   D. 5或如图，已知E是菱形ABCD的边BC上一点，且∠DAE＝∠B＝80°，那么∠CDE的度数为（ C ）A. 20°  B.  25°  C.  30°  D.  35° 平行四边形的一边的长为10cm，则这个平行四边形的两条对角线的长可以是（ D ）A. 4cm，6cm  B. 6cm，8cm   C. 8cm，10cm   D. 10cm，12cm如图，在平行四边形ABCD中，剪去大小不同的平行四边形EGFC，得到另两个图形，三个图形分别标上（L）、（M）、（N），记周长分别为l、m、n，则必有（ C ）                 B.   C.   D. 无法确定 二、     填空题（每小题4分，共24分）函数的自变量取值范围是__x>3______。如图，斜折一页书的一角，使点A落在同一页书内的A＇处，DE为折痕，作DF平分∠A＇DB，则∠FDE＝___90_____°。菱形ABCD中，∠A＝60°，对角线BD长为7cm，则此菱形周长____28____cm。将一根长24cm的筷子，置于底面直径为5cm，高为12cm的圆柱形水杯中，设筷子露在杯子外面的长度为hcm，则h的最小值是_____11___cm。一个平行四边形的周长为70cm，两边的差是9cm，则平行四边形较大边长为___22__cm。实数a在数轴上的位置如图所示，化简__1___。三、     解答题（本大题共6小题，共66分。解答应写出文字说明、演算步骤或推理过程）（5分）先化简，再求值：，其中。解：原式＝    （5分）在△ABC中，∠B＝45°，AB＝，∠A＝105°，求△ABC的面积。解：    （6分）如图，在平行四边形ABCD中，线段AE，BF分别平分∠DAB和∠ABC，交CD于点E，F，线段AE，BF相交于点M。（1）          试说明：AE⊥BF；（2）          判断线段DF与CE的大小关系，并予以说明。解：（1）证明：方法一：如图①，∵在▱ABCD中，AD∥BC，
∴∠DAB＋∠ABC＝180°．（1分）
∵AE、BF分别平分∠DAB和∠ABC，
∴∠DAB＝2∠BAE，∠ABC＝2∠ABF．（2分）
∴2∠BAE＋2∠ABF＝180°．
即∠BAE＋∠ABF＝90°．（3分）
∴∠AMB＝90°．
∴AE⊥BF．（4分） 方法二：如图②，延长BC、AE相交于点P，
∵在▱ABCD中，AD∥BC，
∴∠DAP＝∠APB．（1分）
∵AE平分∠DAB，
∴∠DAP＝∠PAB．（2分）
∴∠APB＝∠PAB．
∴AB＝BP．（3分）
∵BF平分∠ABP，
∴AP⊥BF，
即AE⊥BF．（4分） （2）方法一：线段DF与CE是相等关系，即DF＝CE，（5分）
∵在▱ABCD中，CD∥AB，
∴∠DEA＝∠EAB．
又∵AE平分∠DAB，
∴∠DAE＝∠EAB．
∴∠DEA＝∠DAE．
∴DE＝AD．（6分）
同理可得，CF＝BC．（7分）
又∵在▱ABCD中，AD＝BC，
∴DE＝CF．
∴DE－EF＝CF－EF．
即DF＝CE．（8分）
方法二：如图，延长BC、AE设交于点P，延长AD、BF相交于点O，
∵在▱ABCD中，AD∥BC，
∴∠DAP＝∠APB．
∵AE平分∠DAB，
∴∠DAP＝∠PAB．
∴∠APB＝∠PAB．
∴BP＝AB．
同理可得，AO＝AB．
∴AO＝BP．（6分）
∵在▱ABCD中，AD＝BC，
∴OD＝PC．
又∵在▱ABCD中，DC∥AB，
∴△ODF∽△OAB，△PCE∽△PBA．（7分）
∴，。
∴DF＝CE．（8分） （6分）如图，四边形ABCD是正方形，点E，K分别在BC，AB上，点G在BA的延长线上，且CE＝BK＝AG。（3）          请直接写出DE与DG有怎样的关系____DE＝DG且DE⊥DG______________（2分）（4）          以线段DE，DG为边作出正方形DEFG，连接KF，猜想并写出四边形CEFK是怎样的特殊四边形，并证明你的猜想；（4分） （2）四边形CEFK为平行四边形，
证明：设CK、DE相交于M点， 
∵四边形ABCD和四边形DEFG都是正方形， 
∴AB∥CD，AB＝CD，EF＝DG，EF∥DG， 
∵BK＝AG， 
∴KG＝AB＝CD， 
∴四边形CKGD是平行四边形， 
∴CK＝DG＝EF，CK∥DG， 
∴∠KME＝∠GDE＝∠DEF＝90°， 
∴∠KME＋∠DEF＝180°， 
∴CK∥EF， 
∴四边形CEFK为平行四边形；（11分）如图，货船以20海里每小时的速度将一批货物由A运往正西方的B处，经16小时的航行到达，到达后立即卸货，但此时一台风中心正以40海里每小时的速度由A向北偏西60°的方向移动，距台风中心200海里的圆形区域会受到影响。（5）          B处是否会受到影响？为什么？（4分）（6）          为了避免受影响，该船应在多少小时内卸完货物？（）（4分）解：（1）如图，过点B作BD⊥AC交AC于点D，
∵在Rt△ABD中，∠BAC＝90°－60°＝30°
∴BD＝AB
∵AB＝20×16＝320海里
∴BD＝×320＝160海里．
∵160＜200，
∴会受台风影响．
（2）在Rt△ADB中，AB＝320海里，BD＝160海里，则AD＝160海里，要使卸货不受台风影响，则必须在点B距台风中心第一次为200海里前卸完货，如图，BE＝200海里，在Rt△BDE中，DE＝海里，则AE＝（160－120）海里，台风速度为40海里/小时，则时间t＝小时，
所以为避免受到台风影响，该船应在小时内卸完货．
    （10分）梯形ABCD中，AD∥BC，∠B＝90°，AB＝8cm，AD＝18cm，BC＝24cm，点P从点A开始沿AD边向点D以1cm/s的速度移动，点Q从点C开始沿CB向点B以2cm/s的速度移动，如果P、Q分别从A、C同时出发，设移动时间为t。（7）          当t为何值时，四边形ABPQ为矩形？并求出它的面积。（4分）（8）          当t为何值时，四边形PQCD为平行四边形？（3分）（9）          是否存在某一时刻t使得PQ将梯形ABCD的周长平分为相等的两部分？若存在，求出t的值；若不存在，说明理由。（3分）解：（1）t＝24－2t即t＝8；S四边形ABPQ＝64（2）18－t＝2t即t＝6（3）存在，t＋8＋24－2t＝18－t＋10＋2t即t＝2