北师大九下数学 解题技巧专题：解决抛物线中与系数a，b，c有关的问题

解题技巧专题：解决抛物线中与系数

a，b，c有关的问题

类型一　由已知函数的图象确定其他函数图象的位置

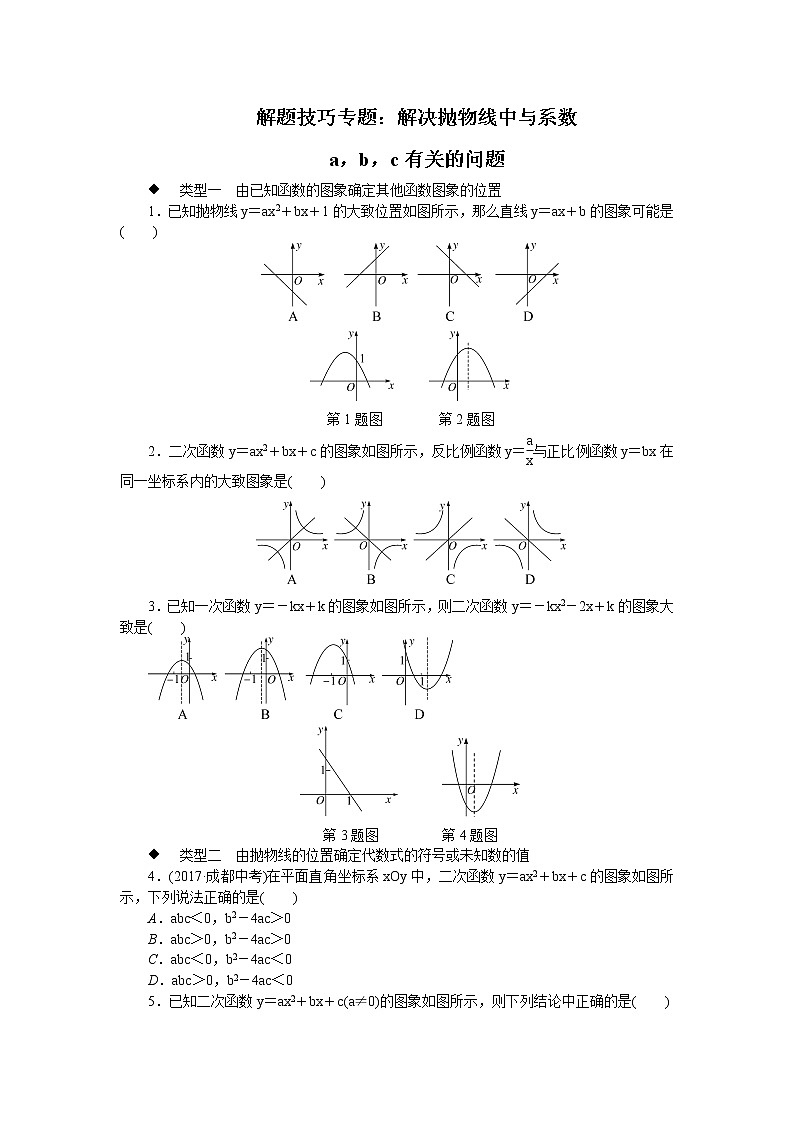
1．已知抛物线y＝ax2＋bx＋1的大致位置如图所示，那么直线y＝ax＋b的图象可能是(　　)

第1题图        第2题图

2．二次函数y＝ax2＋bx＋c的图象如图所示，反比例函数y＝与正比例函数y＝bx在同一坐标系内的大致图象是(　　)

3．已知一次函数y＝－kx＋k的图象如图所示，则二次函数y＝－kx2－2x＋k的图象大致是(　　)

第3题图         第4题图

类型二　由抛物线的位置确定代数式的符号或未知数的值

4．(2017·成都中考)在平面直角坐标系xOy中，二次函数y＝ax2＋bx＋c的图象如图所示，下列说法正确的是(　　)

A．abc＜0，b2－4ac＞0

B．abc＞0，b2－4ac＞0

C．abc＜0，b2－4ac＜0

D．abc＞0，b2－4ac＜0

5．已知二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示，则下列结论中正确的是(　　)

A．a＞0

B．c＜0

C．3是方程ax2＋bx＋c＝0的一个根

D．当x＜1时，y随x的增大而减小

第5题图       第6题图

6．(2017·烟台中考)二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示，对称轴是直线x＝1，下列结论：①ab＜0；②b2＞4ac；③a＋b＋2c＜0；④3a＋c＜0.其中正确的是(　　)

A．①④  B．②④

C．①②③  D．①②③④

7．(2017·营口一模)函数y＝x2＋bx＋c与y＝x的图象如图所示，有以下结论：①b2－4c＞0；②b＋c＋1＝0；③3b＋c＋6＝0；④当1＜x＜3时，x2＋(b－1)x＋c＜0.其中正确的是________(填序号)．

8．二次函数y＝ax2＋bx＋c的图象如图所示，且P＝|2a＋b|＋|3b－2c|，Q＝|2a－b|－|3b＋2c|，比较P，Q的大小关系．

参考答案与解析

1．A

2．C　解析：由y＝ax2＋bx＋c的图象开口向下，对称轴在y轴右侧，得a＜0，－＞0，∴b＞0，∴反比例函数y＝的图象位于第二、四象限，正比例函数y＝bx的图象位于第一、三象限．故选C.

3．B　解析：由一次函数的图象可知k＞1，∴－k＜0，－1<－<0，∴抛物线开口向下，对称轴在直线x＝－1与y轴之间，与y轴的交点在(0，1)的上方．故选B.

4．B　5.C　6.C

7．③④　解析：∵二次函数y＝x2＋bx＋c与x轴无交点，∴b2－4ac＜0，故①错误；当x＝1时，y＝1＋b＋c＝1，故②错误；∵当x＝3时，y＝9＋3b＋c＝3，∴3b＋c＋6＝0，故③正确；∵当1＜x＜3时，二次函数值小于一次函数值，∴x2＋bx＋c＜x，∴x2＋(b－1)x＋c＜0，故④正确．故正确的为③④.

8．解：∵抛物线的开口向下，对称轴在y轴右侧，∴a＜0，－＞0，∴b＞0，∴2a－b＜0.∵－＝1，∴2a＋b＝0，a＝－b.当x＝－1时，y＝a－b＋c＜0，∴－b－b＋c＜0，∴3b－2c＞0.∵抛物线与y轴的正半轴相交，∴c＞0，∴3b＋2c＞0，∴P＝|2a＋b|＋|3b－2c|＝3b－2c，Q＝|2a－b|－|3b＋2c|＝b－2a－3b－2c＝－2a－2b－2c，∴Q－P＝－2a－2b－2c－3b＋2c＝－2a－5b＝－4b＜0，∴P＞Q.