北师大九下数学 类比归纳专题：圆中求阴影部分的面积

类比归纳专题：圆中求阴影部分的面积

——全面掌握核心方法，以不变应万变

类型一　直接利用规则图形的和差求面积

1．如图，在边长为4的正方形ABCD中，先以点A为圆心，AD的长为半径画弧，再以AB边的中点为圆心，AB长的一半为半径画弧，则阴影部分面积是________(结果保留π)．

第1题图         第2题图

2．如图，长方形ABCD的长BC为3cm，宽AB为2cm，点E，F是边AD的三等分点，点G，H是边BC的三等分点．现分别以B，G两点为圆心，以2cm长为半径画弧AH和弧EC，则阴影部分的面积为________cm2.

3．如图，C为半圆内一点，O为圆心，直径AB长为2cm，∠BOC＝60°，∠BCO＝90°，将△BOC绕圆心O逆时针旋转至△B′OC′，点C′在OA上，求边BC扫过区域(图中阴影部分)的面积．

类型二　割补法

4．如图，在扇形AOB中，∠AOB＝90°，正方形CDEF的顶点C是的中点，点D在OB上，点E在OB的延长线上，当正方形CDEF的边长为2时，则阴影部分的面积为________．

   第4题图          第5题图

5．如图所示，正方形ABCD对角线AC所在直线上有一点O，OA＝AC＝2，将正方形绕O点顺时针旋转60°，在旋转过程中，正方形扫过的面积是________．

类型三　等积法

一、轴对称、旋转

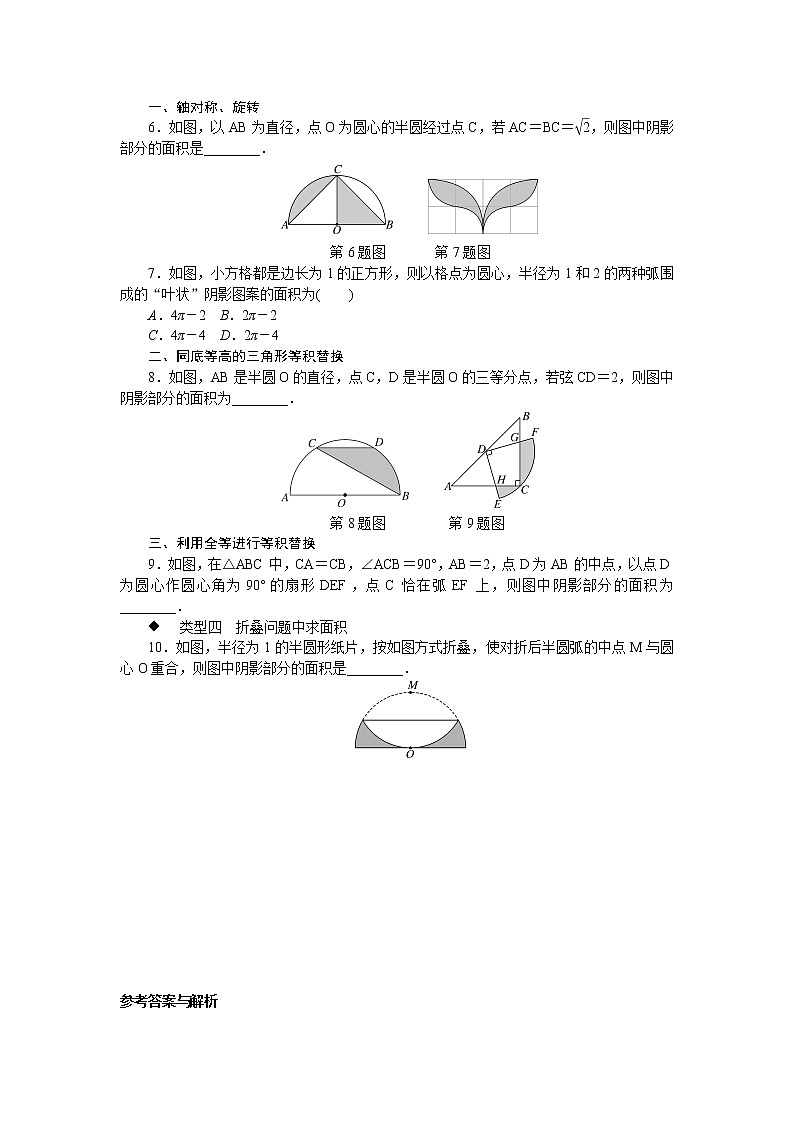
6．如图，以AB为直径，点O为圆心的半圆经过点C，若AC＝BC＝，则图中阴影部分的面积是________．

第6题图       第7题图

7．如图，小方格都是边长为1的正方形，则以格点为圆心，半径为1和2的两种弧围成的“叶状”阴影图案的面积为(　　)

A．4π－2  B．2π－2

C．4π－4  D．2π－4

二、同底等高的三角形等积替换

8．如图，AB是半圆O的直径，点C，D是半圆O的三等分点，若弦CD＝2，则图中阴影部分的面积为________．

  第8题图         第9题图

三、利用全等进行等积替换

9．如图，在△ABC中，CA＝CB，∠ACB＝90°，AB＝2，点D为AB的中点，以点D为圆心作圆心角为90°的扇形DEF，点C恰在弧EF上，则图中阴影部分的面积为________．

类型四　折叠问题中求面积

10．如图，半径为1的半圆形纸片，按如图方式折叠，使对折后半圆弧的中点M与圆心O重合，则图中阴影部分的面积是________．

参考答案与解析

1．2π

2．2　解析：∵四边形ABCD是矩形，点E，F是边AD的三等分点，点G，H是边BC的三等分点，BC＝3cm，∴AE＝EF＝BG＝GH＝1cm，四边形ABGE是矩形．∴S阴影＝S矩形ABGE＋S扇形EGC－S扇形ABH＝S矩形ABGE＝2×1＝2(cm2)．

3．解：由题意，得△B′OC′≌△BOC.∵∠BCO＝90°，∠BOC＝60°，∴∠B′C′O＝90°，∠B′OC′＝60°，∴∠B′OC＝60°，∠C′B′O＝30°，∴∠B′OB＝120°.∵AB＝2cm，∴OB＝1cm，∴OC＝cm，∴S扇形B′OB＝＝(cm2)，S扇形C′OC＝＝(cm2)，∴S阴影＝S扇形B′OB＋S△B′C′O－S△BCO－S扇形C′OC＝S扇形B′OB－S扇形C′OC＝－＝(cm2)．

4．2π－4　5.2π＋2

6.　解析：∵AB为⊙O的直径，∴∠ACB＝90°.∵AC＝BC＝，∴△ACB为等腰直角三角形，∴OC⊥AB，∴△AOC和△BOC都是等腰直角三角形，∴S△AOC＝S△BOC，OA＝AC＝1，∴S阴影＝S扇形AOC＝＝.

7．D　解析：如图，连接AB.由题意得阴影部分的面积为2(S扇形AOB－S△AOB)＝2＝2π－4.故选D.

8. 　解析：连接OC，OD，BD.∵点C，D是半圆O的三等分点，∴∠AOC＝∠COD＝∠DOB＝60°.∵OC＝OD＝OB，∴△COD，△OBD是等边三角形，∴∠COD＝∠ODB＝60°，OD＝CD＝2，∴OC∥BD，∴S△BDC＝S△BDO，∴S阴影＝S扇形OBD＝＝.

9.－　解析：连接CD，过点D作DM⊥BC于点M，作DN⊥AC于点N.∵CA＝CB，∠ACB＝90°，点D为AB的中点，∴DC＝AB＝1，四边形DMCN是矩形，CD平分∠ACB，∴DM＝DN，∴四边形DMCN是正方形．在Rt△CDN中，DC＝1，∠DCN＝45°，∴DN＝.∵∠GDH＝∠MDN＝90°，∴∠GDM＝∠HDN.在△DMG和△DNH中，∴△DMG≌△DNH(ASA)，∴S四边形DGCH＝S四边形DMCN＝＝.∴S阴影＝S扇形FDE－S四边形DGCH＝－＝－.

10.－　解析：如图，连接OM交AB于点C，连接OA，OB.由题意，得OM⊥AB，OC＝MC＝.在Rt△AOC中，∵OA＝1，OC＝，∴cos∠AOC＝＝，AC＝＝，∴∠AOC＝60°，AB＝2AC＝，∴∠AOB＝2∠AOC＝120°，∴S弓形ABM＝S扇形OAB－S△AOB＝－××＝－，∴S阴影＝S半圆O－2S弓形ABM＝π×12－2＝－.