人教版八年级数学下册 第十七章 勾股定理单元检测卷（含解析）

这是一份人教版八年级数学下册 第十七章 勾股定理单元检测卷（含解析），文件包含精品解析人教版八年级下册第十七章勾股定理单元练习题解析版docx、精品解析人教版八年级下册第十七章勾股定理单元练习题原卷版docx等2份试卷配套教学资源，其中试卷共27页， 欢迎下载使用。

第十七章勾股定理
一、选择题
1. 在平静的湖面上，有一支红莲，高出水面1米，一阵风吹来，红莲移到一边，花朵齐及水面，已知红莲移动的水平距离为2米，这里的水深为(　　)
A. 1.5米 B. 2米 C. 2.5米 D. 1米
【1题答案】
【答案】A
【解析】
【分析】设水深为h，则红莲的高h+1，因风吹花朵齐及水面，且水平距离为2m，那么水深h与水平2组成一个以h+1为斜边的直角三角形，根据勾股定理即可求出答案．
【详解】解：设水深为h米，则红莲的高（h+1）米，且水平距离为2米，
则(h+1)2=22+h2，
解得h=1.5．
故选A．
【点睛】此题主要考查学生对勾股定理的应用这一知识点的理解和掌握，此题的关键是“水深h与红莲移动的水平距离为2米组成一个以(h+1)米为斜边的直角三角形”这是此题的突破点，此题难度不大，属于中档题．
2. 小亮想了解旗杆的高度，于是升旗的绳子拉倒旗杆底端，绳子末端刚好接触到地面，然后将绳子末端拉到距离旗杆6 m处，发现此时绳子末端距离地面1 m，则旗杆的高度(滑轮上方的部分忽略不计)为(　　)

A. 17 m
B. 17.5 m
C. 18 m
D. 18.5 m
【2题答案】
【答案】D
【解析】
【分析】根据题意画出示意图，设旗杆高度为x，则AC=AD=x，AB=（x-1）m，BC=6m，在Rt△ABC中利用勾股定理可求出x即可．
【详解】设旗杆高度为x，则AC=AD=x，AB=（x-1）m，BC=6m，
在Rt△ABC中，AB2+BC2=AC2，即（x-1）2+62=x2，
解得：x=18.5，
即旗杆的高度为18.5米，
故选D．

【点睛】本题考查了勾股定理的应用，解答本题的关键是构造直角三角形，构造直角三角形的一般方法就是作垂线．
3. 如图：已知△ABC为直角三角形，分别以直角边AC、BC为直径作半圆AmC和BnC，以AB为直径作半圆ACB，记两个月牙形阴影部分的面积之和为S1，△ABC的面积为S2，则S1与S2的大小关系为（　　）

A. S1＞S2 B. S1＜S2 C. S1=S2 D. 不能确定
【3题答案】
【答案】C
【解析】
【分析】结合图形可知，S1=π（AC）2+π（BC）2-π（AB）2+S△ABC，S2=S△ABC，根据勾股定理可得BC2+AC2=AB2，由此即可求得S1=S2.
【详解】在Rt△ABC中，根据勾股定理可得，BC2+AC2=AB2，
∴S1=π（AC）2+π（BC）2-π（AB）2+S△ABC=π（BC2+AC2-AB2）+S△ABC=S△ABC，
∵S2=S△ABC．
∴S1=S2．
故选C．
【点睛】本题考查勾股定理的知识，正确找出各个图形之间的关系是解决问题的关键．
4. 如图是某地一的长方形大理石广场示意图，如果小琴要从A角走到C角，至少走( )米

A. 90 B. 100 C. 120 D. 140
【4题答案】
【答案】B
【解析】
【分析】由于两点之间线段最短，因此小红所走的最短距离实际是AC的长；根据矩形的性质知△ACD是直角三角形，已知了两条直角边的长，即可由勾股定理求出斜边AC的长．
【详解】解：∵四边形ABCD是矩形，
∴∠D=90°，
Rt△ACD中，AD=60m，CD=80m，
根据勾股定理，得
，
故选：B．
【点睛】此题主要考查了矩形的性质以及勾股定理的应用，解答本题的关键是熟记两点之间线段最短．
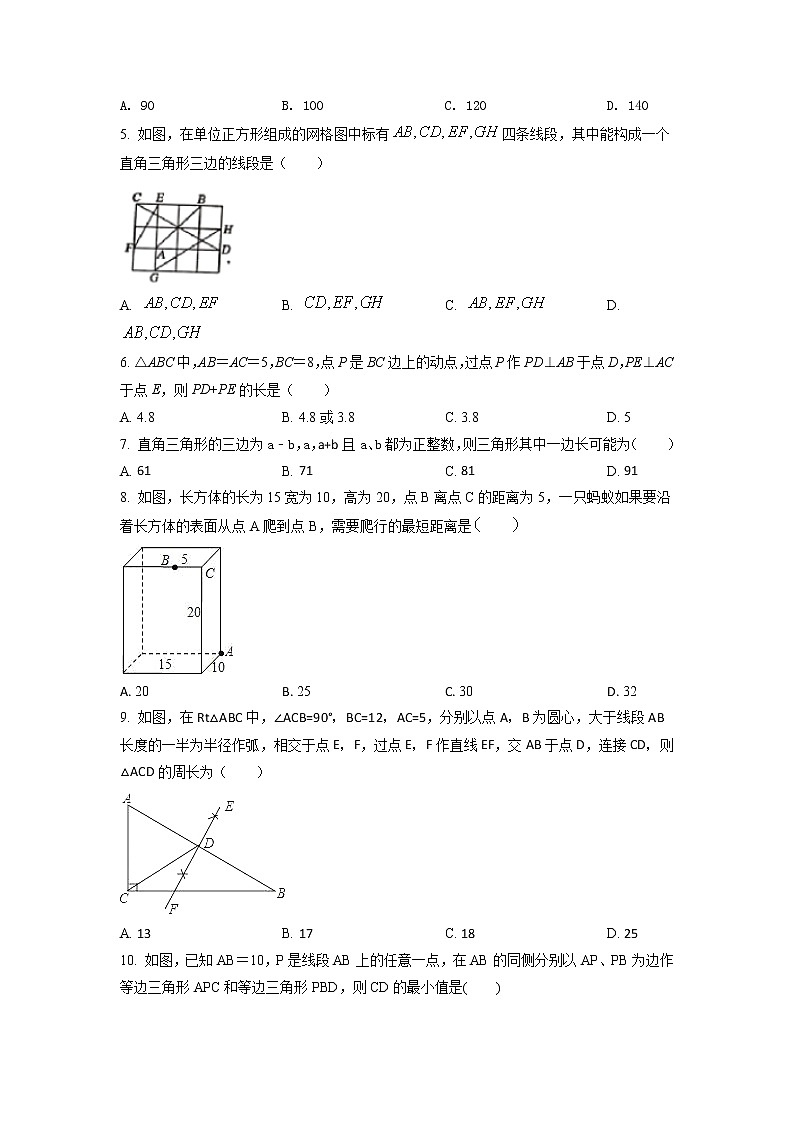
5. 如图，在单位正方形组成的网格图中标有四条线段，其中能构成一个直角三角形三边的线段是（　　）

A. B. C. D.
【5题答案】
【答案】C
【解析】
【分析】设出正方形的边长，利用勾股定理，解出AB、CD、EF、GH各自的长度的平方（因为逆定理也要计算平方），再由勾股定理的逆定理分别验算，看哪三条边能够成直角三角形．
【详解】设小正方形的边长为1，
则AB2=22+22=8，CD2=22+42=20，
EF2=12+22=5，GH2=22+32=13.
因为AB2+EF2=GH2，
所以能构成一个直角三角形三边的线段是AB、EF、GH.
故选C
【点睛】本题考查勾股定理, 勾股定理的逆定理，能熟练运用勾股定理的计算公式进行计算和运用勾股定理的逆定理进行判断是解决本题的关键.
6. △ABC中，AB＝AC＝5，BC＝8，点P是BC边上的动点，过点P作PD⊥AB于点D，PE⊥AC于点E，则PD+PE的长是（　　）
A. 4.8 B. 4.8或3.8 C. 3.8 D. 5
【6题答案】
【答案】A
【解析】
【分析】过A点作AF⊥BC于F，连结AP，根据等腰三角形三线合一的性质和勾股定理可得AF的长，由图形得SABC＝SABP+SACP，代入数值，解答出即可．
【详解】解：过A点作AF⊥BC于F，连结AP，
∵△ABC中，AB＝AC＝5，BC＝8，
∴BF＝4，
∴△ABF中，AF＝3，
∴，
12＝×5×（PD+PE）
PD+PE＝4.8．

故选A．
【点睛】考查了勾股定理、等腰三角形的性质，解答时注意，将一个三角形的面积转化成两个三角形的面积和；体现了转化思想．

7. 直角三角形的三边为a﹣b，a，a+b且a、b都为正整数，则三角形其中一边长可能为（　　）
A. 61 B. 71 C. 81 D. 91
【7题答案】
【答案】C
【解析】
【详解】由题可知：(a−b)2+a2=(a+b)2，解之得：a=4b，
所以直角三角形三边分别为3b、4b、5b.
当b=27时，3b=81.
故选C.
8. 如图，长方体的长为15宽为10，高为20，点B离点C的距离为5，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是　　

A. 20 B. 25 C. 30 D. 32
【8题答案】
【答案】B
【解析】
【详解】试题解析：将长方体展开，连接A、B，
根据两点之间线段最短，
（1）如图，BD=10+5=15，AD=20，

由勾股定理得：AB=．
（2）如图，BC=5，AC=20+10=30，
由勾股定理得，AB=．

（3）只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形，如图：

∵长方体的宽为10，高为20，点B离点C的距离是5，
∴BD=CD+BC=20+5=25，AD=10，
在直角三角形ABD中，根据勾股定理得：
∴AB=；
由于25＜5＜5，
故选B．
9. 如图，在Rt△ABC中，∠ACB=90°，BC=12，AC=5，分别以点A，B为圆心，大于线段AB长度的一半为半径作弧，相交于点E，F，过点E，F作直线EF，交AB于点D，连接CD，则△ACD的周长为（　　）

A. 13 B. 17 C. 18 D. 25
【9题答案】
【答案】C
【解析】
【详解】在Rt△ABC中，∠ACB=90°，BC=12，AC=5，根据勾股定理求得AB=13.根据题意可知，EF为线段AB的垂直平分线，在Rt△ABC中，根据直角三角形斜边的中线等于斜边的一半可得CD=AD=AB，所以△ACD的周长为AC+CD+AD=AC+AB=5+13=18.故选C.
10. 如图，已知AB＝10，P是线段AB上的任意一点，在AB的同侧分别以AP、PB为边作等边三角形APC和等边三角形PBD，则CD的最小值是(　　)

A. 4 B. 5 C. 6 D. 7
【10题答案】
【答案】B
【解析】
【分析】过C作CE⊥AB于E，过D作DF⊥PB于F，过D作DG⊥CE于G，根据勾股定理可以求得CD=，根据CG的取值范围可以求得CD的最小值，即可解题．
【详解】解：如图，过C作CE⊥AB于E，过D作DF⊥PB于F，过D作DG⊥CE于G．
显然DG=EF=AB=5，CD≥DG，
∴CD=，故CG=0时，CD有最小值，
当P为AB中点时，有CD=DG=5，
所以CD长度的最小值是5．

故选B．
【点睛】本题考查了勾股定理在直角三角形中的灵活运用，等边三角形各边长相等的性质，本题中根据勾股定理计算CD的值是解题的关键．
二、填空题
11. 如图，长方体长、宽、高分别为4cm，3cm，12cm，则BD′=__．

【11题答案】
【答案】13
【解析】
【详解】试题解析：如图，连接BD，

则BD==5cm，
BD′==13cm.
12. 如图，四个全等的直角三角形围成一个大正方形，中间空出的部分是一个小正方形，这样就组成了一个“赵爽弦图”，如果大正方形面积为169，且直角三角形中较短的直角边的长为5，则中间小正方形面积(阴影部分)为________．

【12题答案】
【答案】49
【解析】
【分析】设直角三角形中较长的直角边的长为a，利用勾股定理求得直角边的较长边，进一步求得阴影部分的面积即可．
【详解】解：设直角三角形中较长的直角边的长为a，由题意得
a2+52=169
解得：a=12，
则中间小正方形面积(阴影部分)为(12−5)2=49.
故答案为49.
【点睛】本题考查了勾股定理的应用.
13. 《九章算术》中记载：“今有竹高一丈，未折抵地，去根三尺，问折者高几何？”译文：有一根竹子原高一丈（1丈=10尺），中部有一处折断，竹梢触地面处离竹根3尺，试问折断处离地面多高？我们用线段OA和线段AB来表示竹子，其中线段AB表示竹子折断部分，用线段OB表示竹梢触地处离竹根的距离，则竹子折断处离地面的高度OA是_____尺．

【13题答案】
【答案】4.55
【解析】
【分析】根据题意结合勾股定理得出折断处离地面的长度即可.
【详解】设折断处离地面的高度OA是x尺，据题意可得:x2＋32＝ (10－x) 2,解得: x＝4.55,
故答案为4.55.
【点睛】此题主要考查了勾股定理的应用，根据题意正确应用勾股定理是解题关键.
14. 如图，在一根长90cm的灯管上，缠满了彩色丝带，已知可近似地将灯管看作圆柱体，且底面周长为4cm，彩色丝带均匀地缠绕了30圈，则彩色丝带的总长度为__．

【14题答案】
【答案】150cm
【解析】
【详解】试题解析：如图，彩色丝带总长度为=150cm.

15. 如图，AD=8，CD=6，∠ADC=90°，AB=26，BC=24，该图形的面积等于_____．

【15题答案】
【答案】96
【解析】
【详解】试题解析：如图所示，连接AC ，在Rt△ADC中，CD=6，AD=8，则.
在△ ABC中，AB=26，BC=24，AC=10，则 ,故△ ABC为直角三角形.
.
故本题的正确答案应为96.

16. 如图，学校有一块长方形草坪，有极少数人为了避开拐角走“捷径”，在草坪内走出了一条“路”，他们仅仅少走了________步路（假设步为米），却踩伤了花草．

【16题答案】
【答案】
【解析】
【分析】少走的距离是AC+BC-AB，在直角△ABC中根据勾股定理求得AB的长即可．
【详解】解：如图，

∵在中，，
∴ ，
则少走的距离为：，
∵步为米，
∴少走了步．
故答案为：．
【点睛】本题考查正确运用勾股定理．善于观察题目的信息，掌握勾股定理是解题的关键．
17. 一幢高层住宅楼发生火灾，消防车立即赶到，在距住宅楼9米的B处升起梯搭在火灾窗口（如图），已知云梯长15米，云梯底部距地面2米，发生火灾的住户窗口A离地面有_____米．

【17题答案】
【答案】14##十四
【解析】
【分析】根据AB和AC的长度，构造直角三角形，根据勾股定理就可求出直角边BC的长．
【详解】解：∵AC⊥BC，
∴∠ACB=90°；
根据勾股定理，得
AC===12，
∴AF=AC+CF=12+2=14（米）；
答：发生火灾的住户窗口距离地面14米；
故答案14．
【点睛】本题考查勾股定理应用，善于分析题目的信息是解题的关键．
18. 直角三角形斜边长是5，一直角边的长是3，则此直角三角形的面积为___________．
【18题答案】
【答案】6．
【解析】
【详解】试题分析：∵直角三角形斜边长是5，一直角边的长是3，∴另一直角边长为=4．该直角三角形的面积S=×3×4=6．故答案为6．
考点：勾股定理．
19. 如图P(3,4)是直角坐标系中一点，则P到原点的距离是________．

【19题答案】
【答案】5
【解析】
【分析】根据勾股定理，可得答案．
【详解】解： PO==5，
故填5.
【点睛】本题考查了点的坐标，利用勾股定理是解题关键．
20. 如图，在△ABC中，∠C＝90°，则BC＝______.

【20题答案】
【答案】4
【解析】
【分析】根据勾股定理直接计算即可.
【详解】解：在△ABC中，∠C＝90°，
AB=5 AC=3 BC=
故答案为4.
【点睛】此题重点考察学生对勾股定理的应用，掌握勾股定理是解题的关键.
三、解答题
21. 教材第九章中探索乘法公式时，设置由图形面积的不同表示方法验证了乘法公式．我国著名的数学家赵爽，早在公元3世纪，就把一个矩形分成四个全等的直角三角形，用四个全等的直角三角形拼成了一个大的正方形(如图①)，这个图形称为赵爽弦图，验证了一个非常重要的结论：在直角三角形中两直角边a、b与斜边c满足关系式a2＋b2＝c2，称为勾股定理．


（1）爱动脑筋的小明把这四个全等的直角三角形拼成了另一个大的正方形(如图②)，也能验证这个结论，请你帮助小明完成验证的过程．


（2）小明又把这四个全等的直角三角形拼成了一个梯形(如图③)，利用上面探究所得结论，求当a＝3，b＝4时梯形ABCD的周长．


（3）如图④，在每个小正方形边长为1的方格纸中，△ABC的顶点都在方格纸格点上．请在图中画出△ABC的高BD，利用上面的结论，求高BD的长．


【21~23题答案】
【答案】（1）见解析；
（2）；
（3）作图见解析，BD=
【解析】
【分析】（1）根据四个全等的直角三角形的面积+阴影部分小正方形的面积=大正方形的面积，代入数值，即可证明；
（2）由（1）中结论先求出c的值，再根据周长公式即可得出梯形ABCD的周长；
（3）先根据高的定义画出BD，由（1）中结论求出AC的长，再根据△ABC的面积不变列式，即可求出高BD的长．
【小问1详解】
证明：由图得，××4＋c2＝，
整理，得2＋c2＝2＋2＋2，
即2＋2＝c2；
【小问2详解】
解：∵＝3，＝4，
∴c＝＝5，
梯形ABCD的周长为：＋c＋3＋c＝4＋2c＝4×3＋2×5＝22；
【小问3详解】
解：如图5，BD是△ABC的高．


∵S△ABC＝AC·BD＝AB×3，AC＝＝5，
∴BD＝＝＝.
【点睛】本题考查了用数形结合来证明勾股定理，勾股定理的应用，梯形的周长，三角形的高与面积，关键在于数形结合的思想方法．
22. 为了丰富少年儿童的业余生活，某社区要在如图中的AB所在的直线上建一图书室，本社区有两所学校所在的位置在点C和点D处，CA⊥AB于A，DB⊥AB于B，已知AB=2.5km，CA=1.5km，DB=1.0km，试问：图书室E应该建在距点A多少km处，才能使它到两所学校的距离相等？

【22题答案】
【答案】10km
【解析】
【详解】分析：根据题意表示出AE，EB的长，进而利用勾股定理求出即可．
详解：由题意可得：设AE=xkm，则EB=（2.5﹣x）km．∵AC2+AE2=EC2，BE2+DB2=ED2，EC=DE，∴AC2+AE2=BE2+DB2，∴1.52+x2=（2.5﹣x）2+12，解得：x=1．
答：图书室E应该建在距点A1km处，才能使它到两所学校的距离相等．
点睛：本题主要考查了勾股定理的应用，得出AC2+AE2=BE2+DB2是解题的关键．
23. 如图，在边长为1的小正方形组成的网格中，四边形ABCD的四个顶点都在格点上，请按要求完成下列各题：
(1)线段AB的长为________，BC的长为________，CD的长为________；
(2)连接AC，通过计算说明△ACD和△ABC各是什么特殊三角形．

【23题答案】
【答案】（1） ，5，,；（2）直角三角形．
【解析】
【分析】(1)把线段AB、BC、CD、放在一个直角三角形中利用勾股定理计算即可；
(2)根据勾股定理的逆定理求出AC=AD，即可判断△ACD的形状；由勾股定理的逆定理得出△ABC是直角三角形．
【详解】解：

（1）由勾股定理得AB＝＝，BC＝＝5，CD＝＝2；
(2)∵AC＝＝2，AD＝＝2，
∴AC＝AD，
∴△ACD是等腰三角形；
∵AB2＋AC2＝5＋20＝25＝BC2，
∴△ABC是直角三角形．
【点睛】此题主要考查了勾股定理、勾股定理的逆定理以及等腰三角形的判定；熟练掌握勾股定理是解决问题的关键．
24. 写出如图格点△ABC各顶点的坐标，求出此三角形的周长．

【24题答案】
【答案】A(2，2)、B(-2，-1)、C(3，-2)，面积9.5平方单位
【解析】
【分析】先写出各个顶点的坐标，再根据点坐标求出三角形的周长.
【详解】由图可知，A(2,2)，B(－2，－1)，C(3，－2)．
AB＝＝5，
AC＝＝，
BC＝＝，
故周长＝5＋＋
【点睛】此题重点考察学生对勾股定理的实际应用，找出顶点坐标，熟练勾股定理是解题的关键.
25. 在直角三角形中，两条直角边的长度分别为a和b，斜边长度为c，则a2＋b2＝c2，即两条直角边的平方和等于斜边的平方，此结论称为勾股定理．在一张纸上画两个同样大小的直角三角形ABC和A′B′C′，并把它们拼成如图所示的形状 (点C和A′重合，且两直角三角形的斜边互相垂直)．请利用拼得的图形证明勾股定理．

【25题答案】
【答案】见解析
【解析】
【分析】连接,梯形的面积等于上底加下底的和乘以高除以2，,用字母表示出来,化简后,即可得证.
【详解】如图所示，

在Rt△ABC中，
∵∠1＋∠2＝90°，∠1＝∠3，∴∠2＋∠3＝90°.
又∵∠ACC′＝90°，
∴∠2＋∠3＋∠ACC′＝180°，
∴B，C(A′)，B′在同一条直线上．
又∵∠B＝90°，∠B′＝90°，
∴∠B＋∠B′＝180°，∴AB∥C′B′.
由面积相等得(a＋b)(a＋b)＝ab＋ab＋c2，
即a2＋b2＝c2.
【点睛】本题考查了勾股定理的证明，掌握梯形的面积公式并能正确作出辅助线是解题的关键.
26. 如图，四边形ABCD，AB＝AD＝2，BC＝3，CD＝1，∠A＝90°，求∠ADC的度数．

【26题答案】
【答案】135°.
【解析】
【分析】首先在Rt△BAD中，利用勾股定理求出BD的长，求出∠ADB=45°，再根据勾股定理逆定理在△BCD中，证明△BCD是直角三角形，即可求出答案．
【详解】解　连接BD，
在Rt△BAD中，
∵AB＝AD＝2，
∴∠ADB＝45°，BD＝＝2，
在△BCD中，
DB2＋CD2＝(2)2＋12＝9＝CB2，
∴△BCD是直角三角形，
∴∠BDC＝90°，
∴∠ADC＝∠ADB＋∠BDC＝45°＋90°＝135°.

故答案为135°.
【点睛】此题主要考查了勾股定理以及逆定理的运用，解决问题的关键是求出∠ADB=45°，再求出∠BDC=90°．
27. 已知a，b满足|a﹣|++（c﹣4）2＝0．
（1）求a，b，c的值；
（2）判断以a，b，c为边能否构成三角形？若能构成三角形，此三角形是什么形状？并求出三角形的面积；若不能，请说明理由．
【27题答案】
【答案】（1）a＝，b＝5，c＝4；（2）
【解析】
【分析】（1）根据非负数性质得到方程，解方程即可得到结果；
（2）根据三角形的三边关系，勾股定理的逆定理判断即可．
【详解】(1)∵a，b，c满足|a－|＋＋(c－4)2＝0，
∴|a－|＝0，＝0，(c－4)2＝0，
解得a＝，b＝5，c＝4.
(2)∵a＝，b＝5，c＝4，
∴a＋b＝＋5>4.
∴以a，b，c为边能构成三角形．
∵a2＋b2＝()2＋52＝32＝(4)2＝c2，
∴此三角形是直角三角形．
【点睛】本题考查了勾股定理的逆定理，非负数的性质，熟练掌握勾股定理的逆定理是解题的关键．
28. 如图，CD是△ABC的中线，CE是△ABC的高，若AC＝9，BC＝12，AB＝15.
(1)求CD的长．
(2)求DE的长．

【28题答案】
【答案】(1)7.5;(2)2.1.
【解析】
【分析】（1）利用勾股定理的逆定理得到三角形ABC为直角三角形，再根据直角三角形的性质可求CD的长．
（2）根据三角形的面积公式可求CE，再根据勾股定理可求DE的长．
【详解】(1)由AC＝9，AB＝15，BC＝12，
AC2＋BC2＝81+144== AB2
∴∠ACB＝90°，
∵点D是AB的中点，
∴CD＝AB＝7.5；
(2)由∠ACB＝90°，可得S△ABC＝AC·BC＝AB·CE，
∴×9×12＝×15CE，
解得CE＝7.2，
Rt△CDE中，DE＝＝2.1.
故答案为(1)7.5;(2)2.1.
【点睛】本题考查勾股定理的逆定理.