

所属成套资源:人教版新高考数学二轮复习习题训练
人教版新高考数学二轮复习习题训练--题型专项练4 解答题组合练(A)
展开这是一份人教版新高考数学二轮复习习题训练--题型专项练4 解答题组合练(A),共10页。试卷主要包含了已知双曲线C,故an=12n-1等内容,欢迎下载使用。
题型专项练4 解答题组合练(A)
1.(2021·福建福州一模)在△ABC中,内角A,B,C所对的边分别为a,b,c,a+b=ccos B-bcos C.
(1)求角C的大小;
(2)设CD是△ABC的角平分线,求证:.
2.(2021·山东临沂三模)在数列{an}中,a1=1,an+1=(c>0),且a1,a2,a5成等比数列.
(1)证明:数列是等差数列,并求{an}的通项公式;
(2)设数列{bn}满足bn=(4n2+1)anan+1,其前n项和为Sn,证明:Sn<n+1.
3. (2021·湖南怀化一模)如图,在直三棱柱ABC-A1B1C1中,D为B1B的中点,F为C1D的中点,AC=AB=BC=C1C=2.
(1)若M为AB的中点,求证:FM∥平面A1ACC1;
(2)求二面角F-A1C1-B1的余弦值.
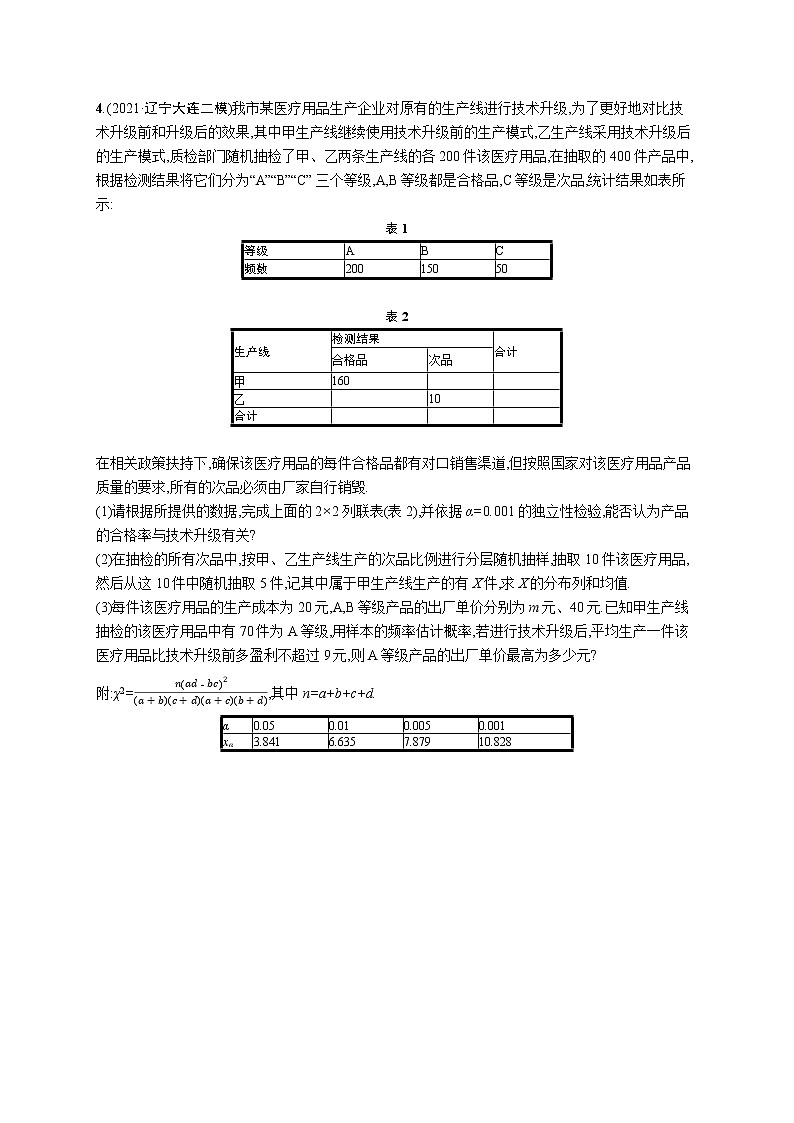
4.(2021·辽宁大连二模)我市某医疗用品生产企业对原有的生产线进行技术升级,为了更好地对比技术升级前和升级后的效果,其中甲生产线继续使用技术升级前的生产模式,乙生产线采用技术升级后的生产模式,质检部门随机抽检了甲、乙两条生产线的各200件该医疗用品,在抽取的400件产品中,根据检测结果将它们分为“A”“B”“C”三个等级,A,B等级都是合格品,C等级是次品,统计结果如表所示:
表1
等级 | A | B | C |
频数 | 200 | 150 | 50 |
表2
生产线 | 检测结果 | 合计 | |
合格品 | 次品 | ||
甲 | 160 |
|
|
乙 |
| 10 |
|
合计 |
|
|
|
在相关政策扶持下,确保该医疗用品的每件合格品都有对口销售渠道,但按照国家对该医疗用品产品质量的要求,所有的次品必须由厂家自行销毁.
(1)请根据所提供的数据,完成上面的2×2列联表(表2),并依据α=0.001的独立性检验,能否认为产品的合格率与技术升级有关?
(2)在抽检的所有次品中,按甲、乙生产线生产的次品比例进行分层随机抽样,抽取10件该医疗用品,然后从这10件中随机抽取5件,记其中属于甲生产线生产的有X件,求X的分布列和均值.
(3)每件该医疗用品的生产成本为20元,A,B等级产品的出厂单价分别为m元、40元.已知甲生产线抽检的该医疗用品中有70件为A等级,用样本的频率估计概率,若进行技术升级后,平均生产一件该医疗用品比技术升级前多盈利不超过9元,则A等级产品的出厂单价最高为多少元?
附:χ2=,其中n=a+b+c+d.
α | 0.05 | 0.01 | 0.005 | 0.001 |
xα | 3.841 | 6.635 | 7.879 | 10.828 |
5.(2021·重庆二模)已知函数f(x)=ex+1+ax2+2ax(a∈R).
(1)若f(x)在区间(-1,+∞)内单调递增,求a的取值范围;
(2)若f(x)存在两个极值点x1,x2(x1<x2),且x2-x1>ln 2,求a的取值范围.
6.(2021·湖南长沙模拟)已知双曲线C:=1(a>0,b>0)的离心率为,双曲线上的点到焦点的最小距离为-2.
(1)求双曲线C的方程;
(2)四边形MNPQ的四个顶点均在双曲线C上,且MQ∥NP,MQ⊥x轴,若直线MN和直线QP交于点S(4,0),四边形MNPQ的对角线交于点D,求点D到双曲线C的渐近线的距离之和.
题型专项练4 解答题组合练(A)
1.(1)解: 由a+b=ccos B-bcos C及正弦定理得sin A+sin B=sin Ccos B-sin Bcos C.
又sin(B+C)=sin(π-A)=sin A,
所以sin(B+C)+sin B=sin Ccos B-sin Bcos C,
所以2sin Bcos C+sin B=0.
因为B∈(0,π),所以sin B≠0,所以cos C=-.
又C∈(0,π),所以C=.
(2)证明: 因为CD是△ABC的角平分线,且C=,所以∠ACD=∠BCD=.
在△ABC中,S△ABC=S△ACD+S△BCD,则CA·CBsinCA·CDsinCD·CBsin,
即CA·CB=CA·CD+CD·CB.
两边同时除以CA·CB·CD得.
2.(1)解: 由a1=1,an+1=,得+c,即=c,所以数列是等差数列,其公差为c,首项为1.
因此=1+(n-1)c,an=.
由a1,a2,a5成等比数列,得=a1a5,即=1×,解得c=2或c=0(舍去).故an=.
(2)证明: 因为bn==1+=1+,
所以Sn=b1+b2+…+bn=n+1-+…+=n+1-.
因为>0,所以Sn<n+1.
3. (1)证明: 如图,取AA1的中点N,连接C1N,ND,取C1N的中点E,连接EF,AE.
∵AN∥BD,AN=BD,
∴四边形ANDB为平行四边形,
∴AB∥ND,AB=ND.
∵E,F分别为C1N,C1D的中点,
∴EF?ND.又AM?ND,∴AM?EF,
∴四边形MAEF为平行四边形,∴MF∥AE.
又MF⊄平面A1ACC1,AE⊂平面A1ACC1,
∴FM∥平面A1ACC1.
(2)解: 如图,建立空间直角坐标系,
则C1(,1,0),F,
∴=(,1,0),.
设平面FA1C1的法向量为n=(x,y,z),则n·x+y=0,n·x+y+z=0,取x=,则y=-3,z=3,∴n=(,-3,3)为平面FA1C1的一个法向量.
由题意可知m=(0,0,1)为平面A1B1C1的一个法向量.
设二面角F-A1C1-B1的平面角为θ,由图可知θ为锐角,
∴cos θ=.
4.解: (1)根据所提供的数据,可得2×2列联表如下.
生产线 | 检测结果 | 合计 | |
合格品 | 次品 | ||
甲 | 160 | 40 | 200 |
乙 | 190 | 10 | 200 |
合计 | 350 | 50 | 400 |
零假设为H0:产品的合格率与技术升级无关.
根据列联表中的数据,
计算可得,χ2=≈20.571>10.828=x0.001,根据小概率值α=0.001的独立性检验,推断H0不成立,即认为产品的合格率与技术升级有关,此推断犯错误的概率不大于0.001.
(2)由于抽检的所有次品中,甲、乙生产线生产的次品数的比为4∶1,
故抽取的10件中有8件是甲生产线生产的,2件是乙生产线生产的,
所以X的所有可能取值为3,4,5,
所以P(X=3)=,P(X=4)=,P(X=5)=,
所以X的分布列为
X | 3 | 4 | 5 |
P |
所以E(X)=3×+4×+5×=4.
(3)甲生产线抽检的产品中有70件A等级,90件B等级,40件C等级,乙生产线抽检的产品中有130件A等级,60件B等级,10件C等级.
用样本的频率估计概率,
则技术升级前,单件产品的利润(单位:元)为m·+40×-20=m-2,
技术升级后,单件产品的利润(单位:元)为m·+40×-20=m-8.
由m-8-≤9,解得m≤50.
故A等级产品的出厂单价最高为50元.
5.解: (1)由题意知f'(x)=ex+1+2ax+2a≥0在区间(-1,+∞)内恒成立,即2a≥-在区间(-1,+∞)内恒成立.
令h(x)=-(x>-1),则h'(x)=-,
由h'(x)>0,得-1<x<0;由h'(x)<0,得x>0,所以h(x)在区间(-1,0)内单调递增,在区间(0,+∞)内单调递减,所以h(x)≤h(0)=-e,所以2a≥-e,即a≥-.
(2)由题意知,x1,x2是方程f'(x)=0的两根,
又f'(-1)=1≠0,
故x1,x2是-=2a的两根,令h(x)=-,
由(1)知h(x)在区间(-∞,-1)和(-1,0)内单调递增,在区间(0,+∞)内单调递减,
当x<-1时,h(x)的图象在x轴上方,
当x>-1时,h(x)的图象在x轴下方,此时当x=0时,h(x)取得最大值h(0)=-e,
所以当2a<-e,即a<-时,方程h(x)=2a有两根x1,x2,其中-1<x1<0<x2.
若x1+ln 2≤0,即-1<x1≤-ln 2,则x2-x1>ln 2一定成立;
若x1+ln 2>0,即x1>-ln 2,则x2-x1>ln 2⇔x2>x1+ln 2⇔h(x2)<h(x1+ln 2),
而h(x2)=h(x1)=2a,所以h(x1)<h(x1+ln 2)⇔-<-,即x1<ln 2-1,
所以-ln 2<x1<ln 2-1.
所以当x2-x1>ln 2时,-1<x1<ln 2-1.
所以2a=h(x1)<h(ln 2-1)=-,所以a<-.
6.解: (1)由题意得解得a2=4,b2=3,所以双曲线C的方程为=1.
(2)如图,由MQ⊥x轴,MQ∥NP,可知四边形MNPQ为等腰梯形,且关于x轴对称,故四边形MNPQ的对角线的交点D在x轴上.
设点D(t,0),则对角线MP的方程为x=my+t(m≠0),
设M(x1,y1),P(x2,y2),由对称性知Q(x1,-y1),N(x2,-y2),
联立消去x得(3m2-4)y2+6mty+3t2-12=0,
所以Δ=(6mt)2-4(3m2-4)(3t2-12)=48(3m2-4+t2)>0,即3m2+t2>4.
由根与系数的关系得y1+y2=,y1y2=,
由M,N,S三点共线知kMS=kNS,即,
所以y1(my2+t-4)+y2(my1+t-4)=0,整理得2my1y2+(t-4)(y1+y2)=0,
所以=0,所以=0,即t=1,所以直线MP过定点(1,0),即D(1,0).
因为双曲线C的渐近线方程为x±2y=0,
所以点D到双曲线C的一条渐近线的距离为,
所以点D到双曲线C的渐近线的距离之和为.
相关试卷
这是一份新高考数学二轮复习题型专项练5解答题组合练(B)含答案,共13页。试卷主要包含了在平面直角坐标系xOy中,已知函数f=a-ln x等内容,欢迎下载使用。
这是一份适用于新高考新教材广西专版2024届高考数学二轮总复习题型专项练4解答题组合练A,共7页。试卷主要包含了如图,已知双曲线C,879等内容,欢迎下载使用。
这是一份2023高考复习专项练习二轮数学 题型专项练5 解答题组合练(B),共10页。试卷主要包含了在平面直角坐标系xOy中,已知函数f=a-ln x等内容,欢迎下载使用。












