2020-2021学年7.1 复数的概念多媒体教学课件ppt

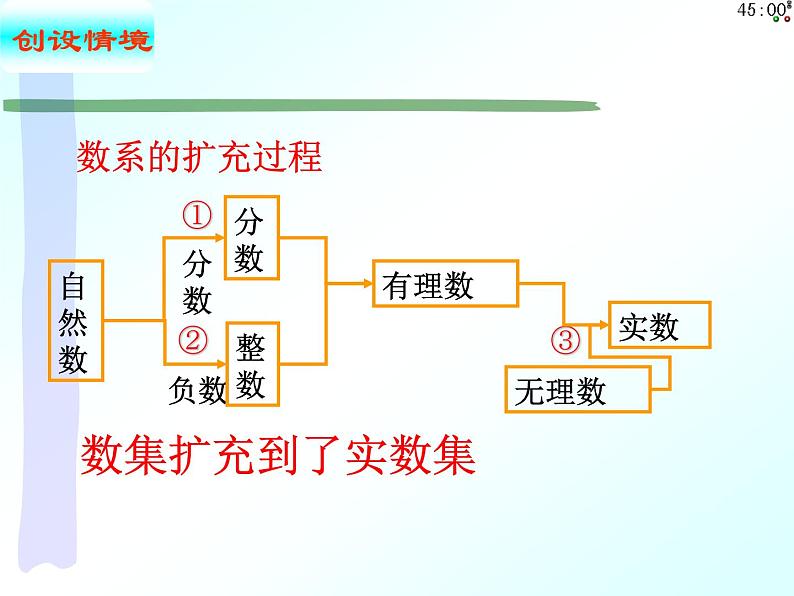
这是一份2020-2021学年7.1 复数的概念多媒体教学课件ppt，共17页。PPT课件主要包含了数系的扩充过程，数集扩充到了实数集，复数的代数形式，试一试，比较探究，复数的分类，复数a＋bi，牛刀小试，－3i，3m＝－2等内容，欢迎下载使用。
①在整数集内解方程3x－2＝0．　 ②在自然数集内解方程x＋3＝0． 　　③在有理数集内解方程 x2－2＝0．
添加负整数，在整数集内方程的根为x＝－3．
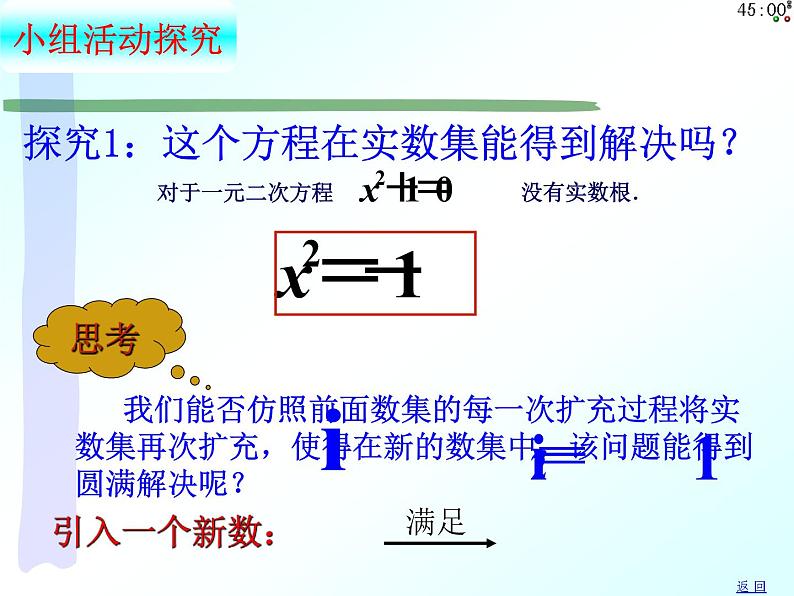
探究1：这个方程在实数集能得到解决吗？
1.复数的概念　形如a＋bi(a，b∈R)的数叫做复数.
全体复数所形成的集合叫做复数集，一般用字母C表示 .
复数通常用字母 z表示，即
规定：（1）i2＝－1； （2）实数可以与 i进行四则运算，在进行四则运算时，原有的加法与 乘法的运算律(包括交换律、结合律和分配律)仍然成立．
把下列式子化为 a+bi（a、bR）的形式，并分别指出它们的实部和虚部。3-2i = ；-2i = ；4= ； 0= .
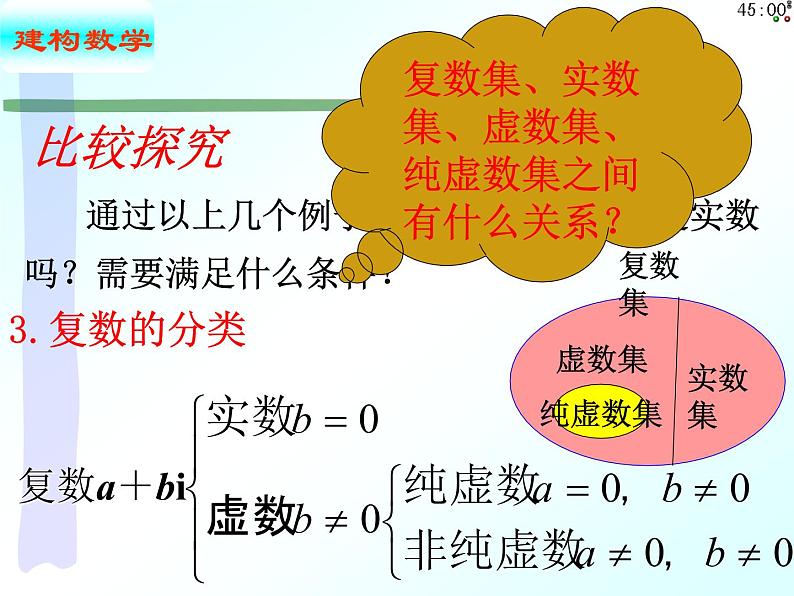
通过以上几个例子，复数z= a+bi可以是实数吗？需要满足什么条件？
复数集、实数集、虚数集、纯虚数集之间有什么关系？
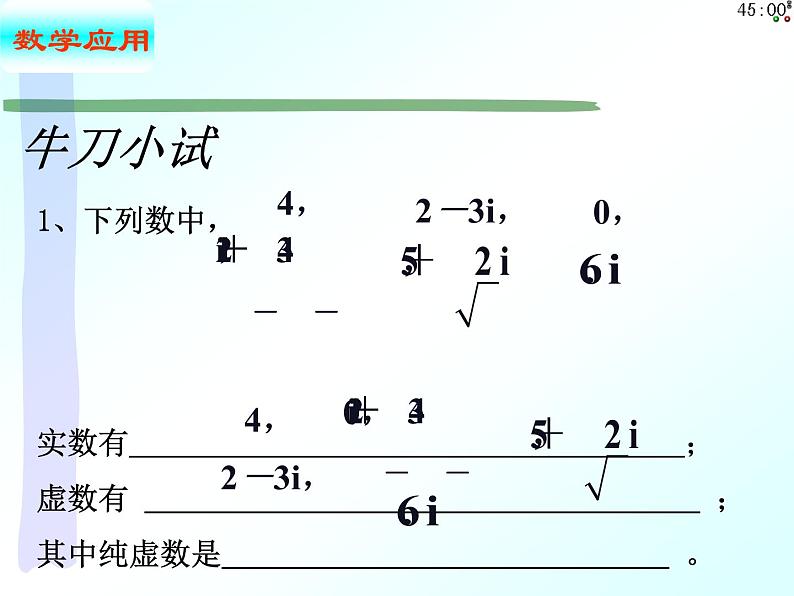
1、下列数中，实数有 ；虚数有 ；其中纯虚数是 。

例1.实数m取何值时，复数 （1）实数？ （2）虚数？（3）纯虚数？
当m为何实数时，复数 是（1）实数 （2）虚数 （3）纯虚数．
思考1　 a ＝ 0 是 z ＝ a ＋ b i(a，bR)为纯虚数的 条件.
探究2：例1中,实数m取什么值时,复数 z 是 6＋2i ?
如果两个复数的实部和虚部分别相等，那么我们就说这两个复数相等．
若a、b、c、d∈R， a+bi=c+di
探究3：两个复数可以比较大小吗?
注意：两个复数只能说相等或不相等，而不能比较大小,但是两个实数可以比较大小。
例2 已知 ，其中x、y∈R , 求x与y的值。
解：根据复数相等的定义，得方程组
例2 已知 ，其中x、y∈R , 求x与y的值。
1、复数的代数形式；2、复数的实部、虚部；3、虚数、纯虚数；4、复数相等：