中考数学：第25课时~多边形及平行四边形-ppt课件

这是一份中考数学：第25课时~多边形及平行四边形-ppt课件，共12页。PPT课件主要包含了平行且相等，互相平分，两条对角线，分别平行，对角分别相等，对边分别相等，两条平行线间的距离，第8题，第9题等内容，欢迎下载使用。
考点一 多边形1.凸多边形：把多边形的任意一条边向两边延长，如果多边形的其他各边都在延长线所得直线的同一侧，这样的多边形叫做凸多边形.注意：一个多边形至少要有三条边.有三条边的叫做三角形；有四条边的叫做四边形；有几条边的叫做几边形.今后所说的多边形，如果不特别声明，都是指凸多边形.2.多边形的对角线条数的计算公式：设多边形的边数为n，则多边形的对角线条数为_________.推论：①多边形的内角和定理：n边形的内角和等于_________________.②多边形的外角和定理：任意多边形的外角和等于_______.
（n－2）·180°
考点二 平行四边形1.平行四边形：两组对边分别平行的四边形叫做平行四边形.平行四边形用符号“□”表示，如平行四边形ABCD记作“□ ABCD”，读作“平行四边形ABCD”.2.平行四边形的性质：（1）平行四边形的邻角______，对角______.（2）平行四边形的对边____________.推论：夹在两条平行线间的平行线段相等.（3）平行四边形的对角线____________.（4）若一直线过平行四边形两条对角线的交点，则这条直线被一组对边截下的线段以对角线的交点为中点，并且这条直线二等分此平行四边形.（5）平行四边形是________对称图形，对称中心是_____________的交点.
3.平行四边形的判定：（1）定义：两组对边___________的四边形是平行四边形.（2）定理1：两组______________的四边形是平行四边形.（3）定理2：两组______________的四边形是平行四边形.（4）定理3：对角线___________的四边形是平行四边形.（5）定理4：一组对边___________的四边形是平行四边形.4.两条平行线间的距离：两条平行线中，一条直线上的任意一点到另一条直线的距离，叫做这___________________.平行线间的距离处处相等.5.平行四边形的面积：S平行四边形＝底×高＝ah.
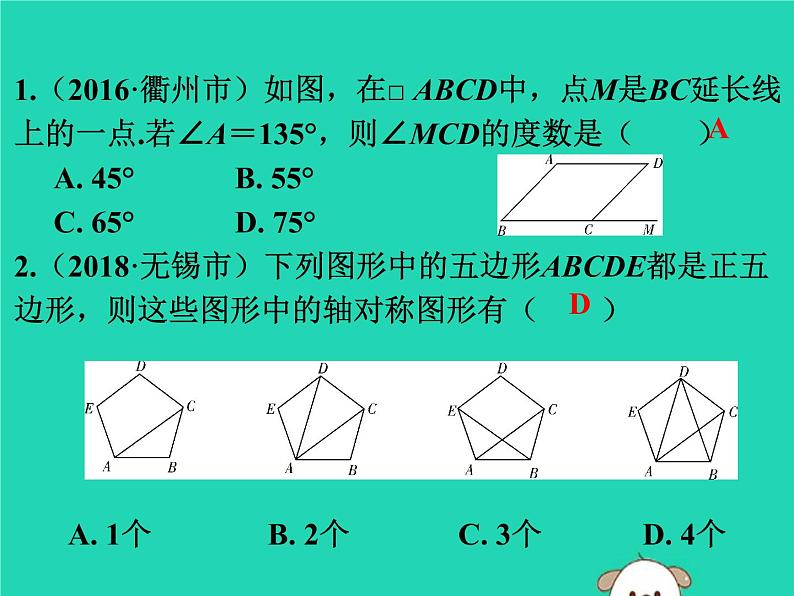
1.（2016·衢州市）如图，在□ ABCD中，点M是BC延长线上的一点.若∠A＝135°，则∠MCD的度数是（ ）A. 45° B. 55°C. 65° D. 75°2.（2018·无锡市）下列图形中的五边形ABCDE都是正五边形，则这些图形中的轴对称图形有（ ） A. 1个 B. 2个 C. 3个 D. 4个
3.（2017·北京市）若正多边形的一个内角是150°，则该正多边形的边数是（ ）A. 6B. 12C. 16D. 184.在四边形ABCD中，对角线AC与BD交于点O，下列条件中，不能判定这个四边形是平行四边形的是（ ）A. OA＝OC，OB＝ODB. AD∥BC，AB∥DCC. AB＝DC，AD＝BCD. AB∥DC，AD＝BC
5.（2017·苏州市）如图，在正五边形ABCDE中，连接BE，则∠ABE的度数为（ ）A. 30° B. 36°C. 54° D. 72°6.（2017·青岛市）如图， □ ABCD的对角线AC与BD相交于点O，AE⊥BC，垂足为E，AB＝ ，AC＝2，BD＝4，则AE的长为（ ）A. B.C. D.
7.（2018·定西市）若正多边形的内角和是1080°，则该正多边形的边数是_______.8.（2016·深圳市）如图，在□ ABCD中，AB＝3，BC＝5，以点B为圆心，以任意长为半径作弧，分别交BA，BC于点P，Q，再分别以点P，Q为圆心，以大于 PQ的长为半径作弧，两弧在∠ABC内交于点M，连接BM并延长交AD于点E，则DE的长为_____.9.（2017·怀化市）如图，在□ ABCD中，OE＝5 cm，则AD的长为____cm.
10.（2018·广东省）如图，BD是菱形ABCD的对角线，∠CBD＝75°.（1）请用尺规作图法，作AB的垂直平分线EF，垂足为E，交AD于点F（不要求写作法，保留作图痕迹）；（2）在（1）的条件下，连接BF，求∠DBF的度数.
解：（1）如图，直线EF即为所求.（2）∵四边形ABCD为菱形，∴BD平分∠ABC，AD∥BC.∵∠CBD＝75°，∴∠ABD＝∠CBD＝∠ADB＝75°. ∴∠A＝180°－75°－75°＝30°.∵EF是AB的垂直平分线，∴AF＝BF，∠ABF＝∠A＝30°. ∴∠DBF＝75°－30°＝45°.
【例题 1】（2016·百色市）如图，在□ ABCD中，CE平分∠BCD且交AD于点E，AF∥CE，且交BC于点F.（1）求证：△ABF≌△CDE；（2）如图，若∠1＝65°，求∠B的大小.
考点：①平行四边形的性质；②全等三角形的判定与性质.
分析：（1）由平行四边形的性质得出AB＝CD，AD∥BC，∠B＝∠D.结合已知条件可证得∠AFB＝∠1，由“AAS”证明△ABF≌△CDE即可.（2）易证得∠DCE＝∠1＝65°，再由平行四边形的性质和三角形内角和定理即可得出结果.
(1)证明：∵四边形ABCD是平行四边形，∴AB＝CD，AD∥BC，∠B＝∠D.∴∠1＝∠BCE.∵AF∥CE，∴∠AFB＝∠BCE.∴∠AFB＝∠1.在△ABF和△CDE中，∴△ABF ≌ △CDE（AAS）.（2）解：由（1）知∠1＝∠BCE.∵CE平分∠BCD，∴∠DCE＝∠BCE.∴∠DCE＝∠1＝65°.∴∠B＝∠D＝180°－2×65°＝50°.