中考数学：第13课时~一次函数的性质及其图象课件PPT

这是一份中考数学：第13课时~一次函数的性质及其图象课件PPT，共16页。PPT课件主要包含了y＝2x－2，是常数k≠0，y＝kx，k为常数k≠0等内容，欢迎下载使用。

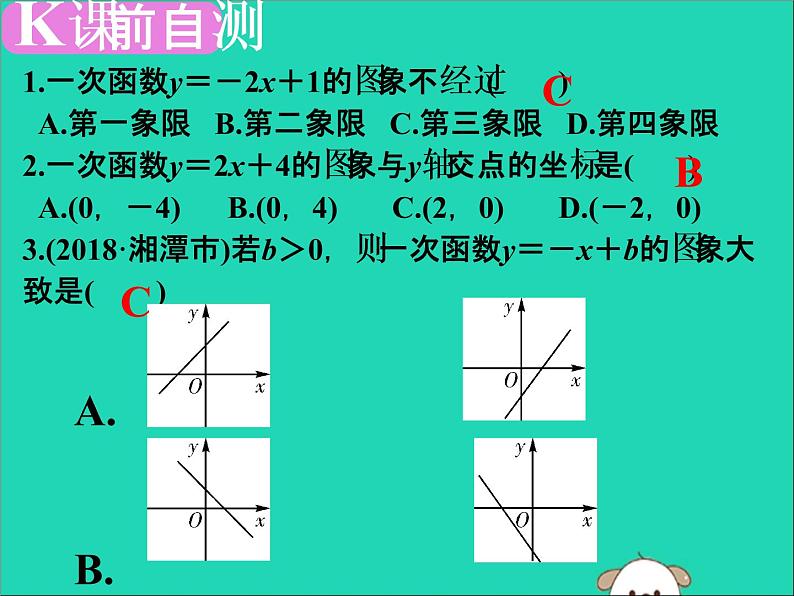
1.一次函数y＝－2x＋1的图象不经过( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限2.一次函数y＝2x＋4的图象与y轴交点的坐标是( ) A.(0，－4) B.(0，4) C.(2，0) D.(－2，0)3.(2018·湘潭市)若b＞0，则一次函数y＝－x＋b的图象大致是( )
A. B.C. D.
4.若一次函数y＝ax＋b的图象经过第一、二、四象限，则下列不等式中总是成立的是( ) A.ab＞0 B.a－b＞0 C.a2＋b＞0 D.a＋b＞05.已知直线y＝kx＋b，若k＋b＝－5，kb＝6，那么该直线不经过( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限6.如图，函数y＝2x和y＝ax＋4的图象相交于点A(m，3)，则不等式2x≥ax＋4的解集为( ) A. x ≥ B. x ≤ 3 C. x≤ D. x ≥ 3
7.(2016·永州市)已知一次函数y＝kx＋2k＋3的图象与y轴的交点在y轴的正半轴上，且函数值y随x的增大而减小，则k所有可能取得的整数值为________.8.(2016·娄底市)将直线y＝2x＋1向下平移3个单位长度后所得直线的解析式是___________.
9.(2016·枣庄市)如图，点A的坐标为(－4，0)，直线 y＝ x＋n与坐标轴交于点B，C，连接AC.若∠ACD＝90°，则n的值为________.10.已知一次函数y＝kx＋b(k，b为常数，且k≠0)的图象经过点A(0，－2)和点B(1，0)，则一次函数的表达式为___________.
11.(2018·无锡市)一水果店是A酒店某种水果的唯一供货商，水果店根据该酒店以往每月的需求情况，本月初专门为他们准备了2600 kg的这种水果.已知水果店每售出1 kg该水果可获利润10元，未售出的部分每1 kg将亏损6元，以x(单位：kg，2000≤x≤3 000)表示A酒店本月对这种水果的需求量，y(元)表示水果店销售这批水果所获得的利润.(1)求y关于x的函数表达式；(2)问：当A酒店本月对这种水果的需求量如何时，该水果店销售这批水果所获得的利润不少于 22000元？
解：(1)由题意，得当2000 ≤ x ≤ 2600时，y＝10x－6(2600－x)＝16x－1560；当2600＜ x ≤ 3 000时，y＝2600×10＝26000.(2)由题意，得16x－15600 ≥ 22 000，解得x ≥ 2350.∴当A酒店本月对这种水果的需求量不超过3000 kg、不少于2350 kg时，该水果店销售这批水果所获得的利润不少于22000元.
考点一 正比例函数和一次函数1.正比例函数和一次函数的概念：一般地，如果两个变量x，y能表示成__________________________________的形式，那么y叫做x的一次函数.特别地，当一次函数y＝kx＋b中的b＝0时，则_______________________ ，这时，y是x的正比例函数.2.一次函数的图象：所有一次函数的图象都是一条______.
y＝kx＋b (k，b
直线位置与k，b的关系： (1)k＞0，直线向上的方向与x轴的正方向所形成的夹角为 __________； (2)k＜0，直线向上的方向与x轴的正方向所形成的夹角为 __________； (3)b＞0，直线与y轴的交点在x轴的 _________； (4)b＝0，直线过 ________； (5)b＜0，直线与y轴的交点在x轴的 ________.3.一次函数、正比例函数图象的主要特征：(1)一次函数y＝kx＋b的图象是一条经过点 _______的直线；(2)正比例函数y＝kx的图象是一条经过 原点_______ 的直线.
考点一 正比例函数和一次函数
4.正比例函数y＝kx的性质： (1)当k>0时，图象经过第__________象限，y随x的增大而_______； (2)当k<0时，图象经过第__________象限，y随x的增大而________.5.一次函数y＝kx＋b的性质： (1)当k>0时，y随x的增大而_______； (2)当k<0时，y随x的增大而________.
考点二 正比例函数和一次函数解析式的确定 确定一个正比例函数，就是要确定正比例函数定义式y＝kx(k≠0)中的常数k. 确定一个一次函数，需要确定一次函数定义式y＝kxb(k≠0)中的常数k和b.解这类问题的一般方法是待定系数法.
考点二 正比例函数和一次函数解析式的确定
【例题1】若关于x的一元二次方程x2－2x＋kb＋1＝0有两个不相等的实数根，则一次函数y＝kx＋b的大致图象可能是( )
A. B. C. D.
考点：①根的判别式；②一次函数的图象.
分析：根据一元二次方程x2－2x＋kb＋1＝0有两个不相等的实数根，得到Δ＞0，求出kb的符号，再对各个图象进行判断即可.
变式：(2017·日照市)已知反比例函数y＝ 的图象如图所示，则一次函数y＝kx＋b(k≠0)的图象大致是( )
A B C D
【例题2】如图，已知直线l1：y＝k1x＋4与直线l2：y＝k2x－5交于点A，它们与y轴的交点分别为点B，C，点E，F分别为线段AB，AC的中点，则线段EF的长度为_______.
考点：①三角形中位线定理；②两条直线相交或平行问题.
分析：根据直线解析式易求得点B，C的坐标，由两点间的距离得到BC的长度.再根据三角形中位线定理来求EF的长度.