中考数学：第15课时~二次函数的性质及其图象课件PPT

这是一份中考数学：第15课时~二次函数的性质及其图象课件PPT，共22页。PPT课件主要包含了y＝ax2＋bx＋c，开口方向a，对称轴，开口方向等内容，欢迎下载使用。

1.抛物线y＝x2－6x＋5的顶点坐标为( ) A. (3，－4) B. (3，4) C. (－3，－4) D. (－3，4)2.如果将抛物线y＝x2向右平移1个单位，那么所得的抛物线的表达式为( ) A. y＝x2－1 B. y＝x2＋1 C. y＝ D. y＝3.(2016·广州市)对于二次函数 ，下列说法正确的是( )A.当x＞0时，y随x的增大而增大 B.当x＝2时，y有最大值－3C.图象的顶点坐标为(－2，－7) D.图象与x轴有两个交点
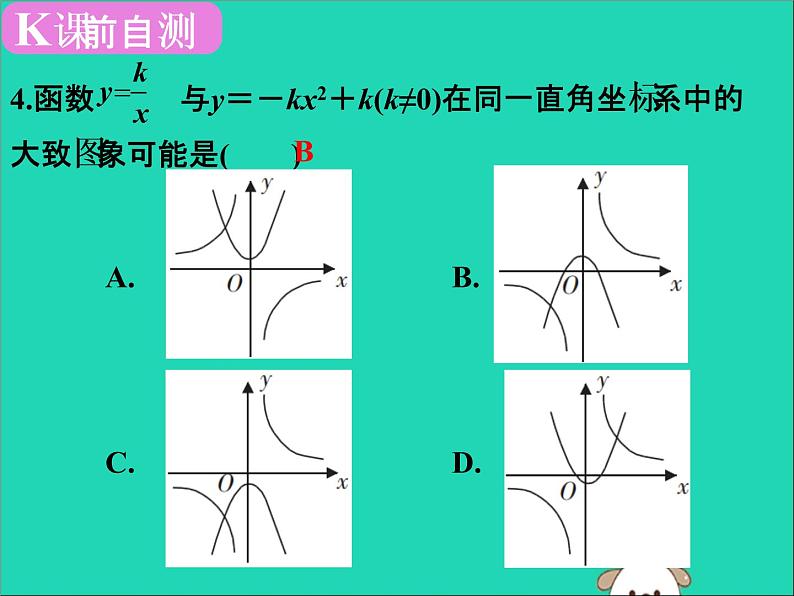
4.函数 与y＝－kx2＋k(k≠0)在同一直角坐标系中的大致图象可能是( )
A. B.C. D.
5.“如果二次函数y＝ax2＋bx＋c的图象与x轴有两个公共点，那么一元二次方程ax2＋bx＋c＝0有两个不相等的实数根.”请根据你对这句话的理解，解决下面的问题：若m，n(m＜n)是关于x的方程 1－(x－a)(x－b)＝0的两根，且a＜b，则a，b，m，n的大小关系是( ) A. m＜a＜b＜n B. a＜m＜n＜b C. a＜m＜b＜n D. m＜a＜n＜b
6.(2018·定西市)如图是二次函数y＝ax2＋bx＋c(a，b，c是常数，a≠0)图象的一部分，与x轴的交点A在点(2，0)和(3，0)之间，对称轴是直线x＝1.下列说法：①ab＜0；②2a＋b＝0；③3a＋c＞0；④a＋b ≥ m(am＋b)(m为实数)；⑤当－1＜x＜3时，y＞0.其中正确的是( ) A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
7.把二次函数y＝x2－12x化为形如y＝a＋k的形式：____________________.8.函数y＝x2＋2x＋1，当y＝0时，x＝______；当1＜x＜2时，y随x的增大而_______(选填“增大”或“减小”).9.已知点A(2，y1)，B(3，y2)是二次函数y＝x2－2x＋1图象上的两点，则y1与y2的大小关系为 y1_____y2(选填“＞”“＜”或“＝”).
y＝(x－6)2－36
10.已知抛物线 ，其中m是常数.(1)求证：不论m为何值，该抛物线与x轴一定有两个公共点.(2)若该抛物线的对称轴为直线 ;①求该抛物线的函数表达式；②把该抛物线沿y轴向上平移多少个单位长度后，得到的抛物线与x轴只有一个公共点？
(1)证明：∵y＝(x－m)2－(x－m)＝(x－m)(x－m－1)，∴令y＝0，得(x－m)(x－m－1)＝0，解得x1＝m，x2＝m＋1.∵m ≠ m＋1，∴不论m为何值，该抛物线与x轴一定有两个公共点.(2)解：①∵y＝(x－m)2－(x－m)＝x2－(2m＋1)x＋m(m＋1)，∴抛物线的对称轴为直线 ,解得m＝2.∴抛物线的函数表达式为y＝x2－5x＋6.②∵ ∴该抛物线沿y轴向上平移 个单位长度后，得到的抛物线与x轴只有一个公共点.
考点一 二次函数的概念和图象1.二次函数的概念：一般地，如果_______________________________________，那么y叫做x的二次函数.2.二次函数的图象：二次函数的图象是一条关于直线 对称的曲线，这条曲线叫做抛物线.抛物线的主要特征：①有___________；②有_________；③有________.3.二次函数图象的画法(五点法)：(1)先根据函数表达式求出顶点坐标，在平面直角坐标系中描出顶点M，并用虚线画出对称轴.
(a，b，c是常数，a ≠ 0)
(2)求抛物线y＝ax2＋bx＋c与坐标轴的交点： ①当抛物线与x轴有两个交点时，描出这两个交点A，B及抛物线与y轴的交点C，再找到点C的对称点D.用平滑曲线将这五个点按从左到右的顺序连接起来，并向上或向下延伸，就得到二次函数的图象. ②当抛物线与x轴只有一个交点或无交点时，描出抛物线与y轴的交点C及对称点D，由C，M，D三点可粗略地画出二次函数的草图.如果需要画出比较精确的图象，可再描出一对对称点A，B，然后用平滑曲线顺次连接五点，得到二次函数的图象.
考点二 二次函数的表达式二次函数的解析式有三种形式：(1)一般式：___________________________________.(2)顶点式：_____________________________，顶点坐标是_________.(3)当抛物线y＝ax2＋bx＋c与x轴有交点时，则对应一元二次方程ax2＋bx＋c＝0有两个实根x1和x2，根据二次三项式的分解因式ax2＋bx＋c＝a，二次函数y＝ax2＋bx＋c可转化为两根式y＝a(x－x1)(x－x2).如果没有交点，则不能这样表示.
y＝ax2＋bx＋c(a，b，c是常数，a≠0)
y＝a＋k(a，h，k是常数，a≠0)
考点三 二次函数的最值如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值(或最小值)，即当x＝ 时，y最值＝ . 如果自变量的取值范围是x1≤x≤x2，那么，首先要看 是否在自变量取值范围x1≤x≤x2内.若在此范围内，则当x＝ 时，y最值＝ .若不在此范围内，则需要考虑函数在x1≤x≤x2范围内的增减性：若在此范围内且y随x的增大而增大，则当x＝x2时，y最大＝ ax2 ＋bx2＋c，当x＝x1时，y最小＝ ax2 ＋bx1＋c；若在此范围内且y随x的增大而减小，则当x＝x1时，y最大＝ ax2 ＋bx1＋c，当x＝x2时，y最小＝ ax2 ＋bx2＋c.
考点四 二次函数的性质1.二次函数的性质：
2.二次函数y＝ax2＋bx＋c(a，b，c是常数，a≠0)中，a，b，c的含义：(1)a决定__________：a>0时，抛物线开口________，a<0时，抛物线开口_______；(2)b与对称轴有关：对称轴为直线__________；(3)c决定抛物线与y轴的交点坐标：_________.
3.二次函数与一元二次方程的关系：一元二次方程的解是其对应的二次函数的图象与x轴交点的横坐标.因此一元二次方程中的判别式Δ＝b2－4ac，决定了二次函数的图象与x轴是否有交点：(1)当Δ>0时，图象与x轴有_____交点；(2)当Δ＝0时，图象与x轴有_____交点；(3)当Δ<0时，图象与x轴_____交点.
补充：1.平面内两点间距离公式(当遇到没有思路的题时，可用此方法拓展思路，以寻求解题方法)：如图，点A坐标为(x1，y1)，点B坐标为(x2，y2)，则AB间的距离，即线段AB的长度为 .2.函数图象平移规律(中考试题中，只占3分，但掌握这个知识点，对提高答题速度有很大帮助，可以大大节省做题的时间)：左加右减，上加下减(函数值加减上下移，自变量加减左右移).
【例题 1】已知函数y＝－(x－m)(x－n)(其中m＜n)的图象如图所示，则一次函数 y＝mx＋n 与反比例函数 的图象可能是( )
A. B.C. D.
考点：①二次函数的图象；②一次函数的图象；③反比例函数的图象.
分析：根据二次函数的图象判断出m＜－1，n＝1，然后求出m＋n＜0，再根据一次函数与反比例函数图象的性质判断即可.
变式：(2017·达州市)已知二次函数y＝ ax2 ＋bx＋c的图象如图所示，则一次函数y＝ax－2b与反比例函数 在同一平面直角坐标系中的图象大致是( )
【例题 2】已知点A(a－2b，2－4ab)在抛物线y＝x2＋4x＋10上，则点A关于抛物线对称轴的对称点坐标为( ) A.(－3，7) B.(－1，7) C.(－4，10) D.(0，10)
考点：①二次函数图象上点的坐标特征；②坐标与图形变化——对称.
分析：把点A的坐标代入二次函数解析式并利用完全平方公式整理，然后根据非负数的性质列式求出a，b，进而可得点A的坐标，然后根据抛物线的对称轴，利用对称的性质求解即可.